9.2.1. Застосування методу січних площин при
На рис.9.3. дані конус і півсфера.
В
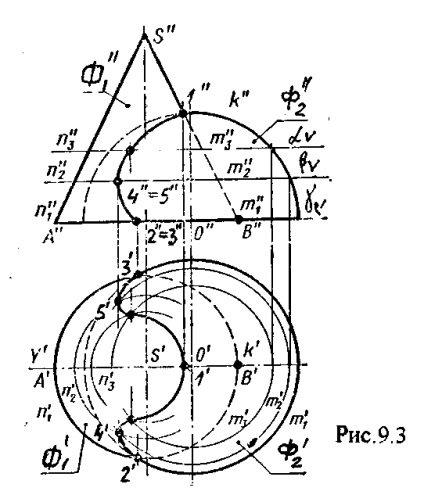
об почати побудову лінії перетину необхідно почати побудову лінії перетину необхідно знайти опор-ні точки: найвищу і найнижчу в даному випадку. В інших випадках це може бути найлівіша або найправіша точки. Перетнемо обидві поверхні площиною V і проходить через осі обертання поверхонь. В результаті отримаємо лінії перетину, які є фронтальними нарисами даних поверхонь. Точка перетину нарисів 1 є точкою, що належить лінії перетину.
Так як підстави обох поверхонь лежать в одній площині, то точки перетину кіл 2 і 3 також є загальними точками для даних поверхонь.
Точки 1,2,3 є опорними, точка 1 - найвища, точки 2, 3 найнижчі. Тепер обидві поверхні перетнемо площиною , розташованої нижче точки 1 і вище точок 2 і 3. Ця площину перетне обидві поверхні по колах n2 і m2 знайдемо точки перетину отриманих кіл n2 m2 = 4. n2 m2 = 5.
Точки 4,5 належать лінії перетину конуса і півсфери. Повторивши цю дію, необхідне число раз, побудуємо лінію перетину даних поверхонь.
9.3. Метод концентричних сфер
В
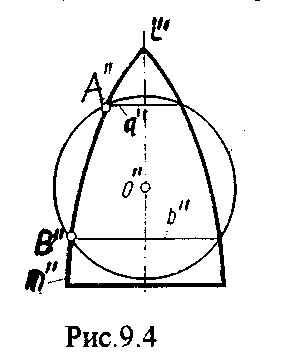
Застосування цього методу засноване на наступному властивості: Дві поверхні обертання, що мають загальну вісь (співвісні поверхні), перетинаються по колах. Дійсно, крива m утворює поверхню обертання з віссю обертання i, крива n утворює другу поверхню обертання з тієї ж віссю i. Якщо mn = А, то точка А опише коло, яка є спільною для обох поверхонь, отже, є лінією їх перетину. (Рис.9.4.)
Якщо вісь i перпендикулярна площині Н, то окружність, що описується точкою А, проектується на фронтальну площину проекцій в відрізок, а на горизонтальну площину в коло.
Зі сказаного можна зробити наступні висновки:
1. Для того, щоб допоміжна січна сфера перетинала по колах дві задані поверхні обертання, центр сфери повинен лежати в точці перетину осей цих поверхонь.
2. Якщо осі заданих поверхонь обертання паралельні площині проекцій, то окружності перетину допоміжної січної сфери з цими поверхнями проектується на цю площину в відрізки.
Тепер можна сформулювати умови, необхідні для застосування методу концентричних січних сфер:
1. Дані поверхні повинні бути поверхнями обертання;
2. Осі обертанні даних поверхонь повинні перетинатися;
3. Площина, що проходить через осі обертання даних поверхонь, повинна бути паралельна який - небудь площині проекцій.
Побудова лінії перетину починається з побудови опорних точок (рис.9.5.). Щоб побудувати опорні точки треба побудувати сферу мінімального радіуса. Сфера мінімального радіуса вписана в одну поверхню і перетинає другу.
Загальні точки С і Д окружності торкання з конусом і окружності перетину з циліндром є опорними точками. До опорних точок відносяться також точки перетину фронтальних нарисів даних поверхонь. Відрізок OF де f найбільш віддалена від точки О точка перетину нарисів даних поверхонь визначає сферу максимального радіуса.
Для побудови проміжних точок необхідно вибрати сферу радіуса R, де Rmin - еліпс