Алгоритми видалення невидимих граней можуть бути умовно поділені на два класи в залежності від принципів, закладених для їх реалізації. Перший клас - це алгоритми працюють в просторі об'єкта. Це означає, що для визначення видимості даної межі порівнюється її взаємне розташування з усіма іншими гранями в тривимірній сцені. Нехай N - кількість граней у тривимірній сцені. Для побудови тривимірної сцени в цьому випадку необхідно порівняти становище кожної грані з рештою, що вимагає порядку
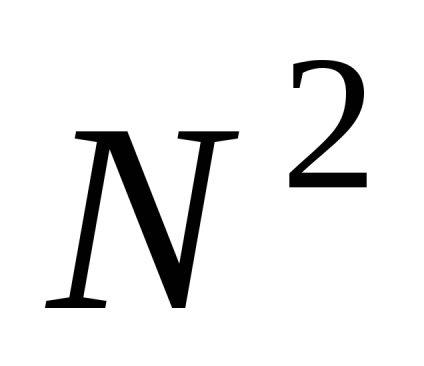
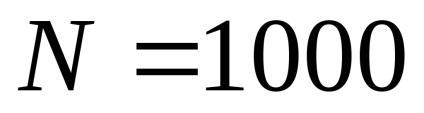
Інший клас алгоритмів - працюють у просторі зображення, заснований на знаходженні точки найближчої межі яку перетинає промінь зору, що проходить через задану точку на растрі. Оскільки число точок на растровому екрані фіксоване, то алгоритми цього класу менш чутливі до збільшення кількості об'єктів в тривимірній сцені. Нехай n - число точок на растровому екране.Тогда кількість операцій, необхідних для побудови тривимірної сцени буде порядку
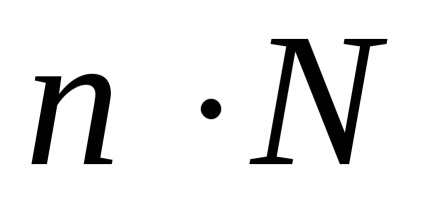

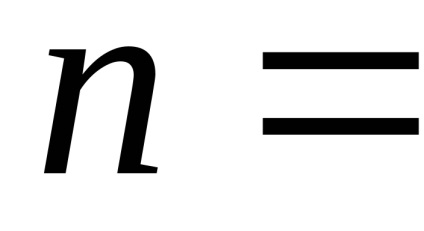
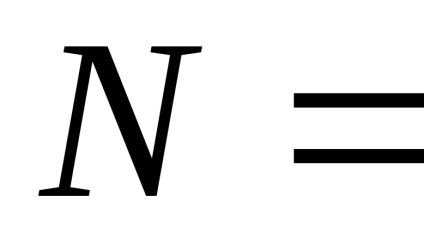
Розглянемо алгоритм видалення невидимих граней з використанням z-буфера, який є одним з найбільш часто використовуваних в сучасних додатках комп'ютерної графіки. Він працює в просторі зображення і застосовується в таких популярних графічних бібліотеках какOpenGL іDirect3D.
Алгоритм працює в паралельній проекції. Нехай розміри вікна виведення або екрану складають X точок в ширину іY точок у висоту. У качествеz -буфера заведемо двовимірний прямокутний масив чисел по розмірності збігається з вікном виведення або екрана, т.е.X

На початку роботи алгоритму в z-буфер заносяться значення, відповідні нескінченності. Кожна грань тривимірного об'єкту, представлена у вигляді багатокутника, перетворюється в растрову форму. При розкладанні в растр для кожної точки багатокутника обчислюється значення ееz-координати. Есліz-координата виявилася менше ніж поточне значення вz-буфері, то вz-буфер заносітсяz-координата точки, і на екрані малюється точка кольором поточного багатокутника. Після розкладання в растр всіх багатокутників зображення тривимірної сцени побудовано.
Розглянемо спосіб прискореного обчислення z-координат при розкладанні багатокутників в растр. Запишемо рівняння площини, утвореної многоугольником в просторі :.
Висловимо z-координату точки:. Нехай. Найдемz-координату для сусідньої точки
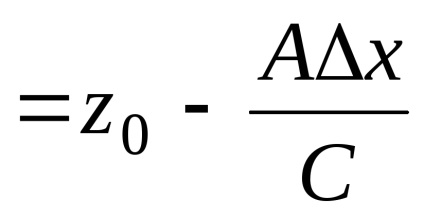
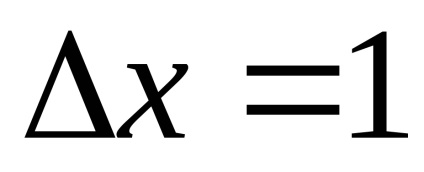
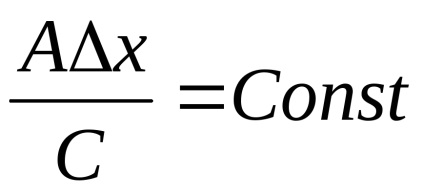
Метод складається з трьох основних етапів:
Впорядкування всіх багатокутників відповідно до їх найбільшими z-координатами.
Дозвіл всіх невизначеностей, які виникають при перекритті z-оболонок багатокутників.
Перетворення кожного з багатокутників в растрову форму, вироблене в порядку зменшення їхньої найбільшої z-координати.
Найближчі багатокутники перетворюються в растрову форму останніми і закривають більш віддалені багатокутники, так як зображуються поверх попередніх. Реалізація пунктів 1 і 3 досить очевидна. Розглянемо докладніше пункт 2.
Нехай багатокутник P після впорядкування знаходиться в кінці списку, тобто є найбільш віддаленим. Все многоугольнікіQчьі оболонки перекриваються Сz-оболочкойP повинні проходити перевірку по п'яти тестів (кроків). Якщо на певному етапі отримано позитивну відповідь, ТОР відразу перетвориться в растрову форму.
x-Оболонки багатокутників не перекриваються, тому самі багатокутники теж не перекриваються.
y-Оболонки багатокутників не перекриваються, тому самі багатокутники теж не перекриваються.
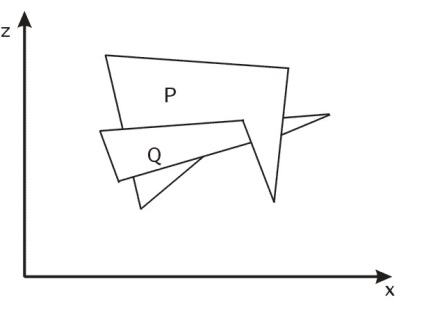
Pполностью розташований з того боку від плоскостіQ, яка далі від точки зору (цей тест дає позитивну відповідь як показано на рис.36 а).
Q повністю розташований з того боку від плоскостіP, яка ближче до точки зору. Цей тест дає позитивну відповідь як показано на рис. 36b).
Проекції багатокутників на площині xOy, тобто на екрані, не перекриваються (це визначається порівнянням ребер одного багатокутника з ребрами іншого).
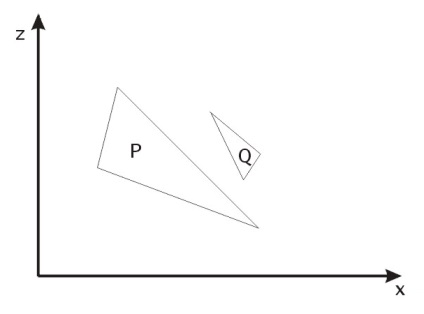
Мал. 35.
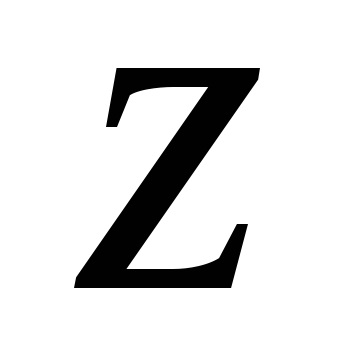
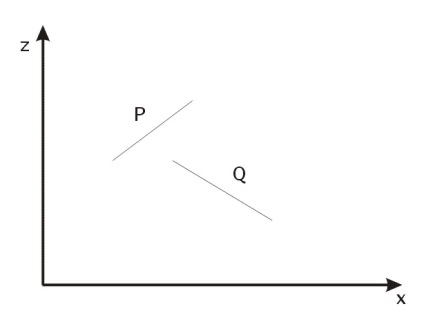
Мал. 36. Взаємні розташування трикутників в просторі.
Якщо у всіх п'яти тестах отримано негативну відповідь, то P - дійсно закриваетQ. Тоді меняемP іQ в списку місцями. У разі, як показано на мал.37, алгоритм зациклюється.
Для уникнення зациклення вводиться обмеження: багатокутник, переміщений в кінець списку (тобто позначений), не може бути повторно переміщений. Замість цього многоугольнікP іліQ розділяється площиною іншого на два нових багатокутника. Ці два нових багатокутника слід включати до місця упорядкованого списку, і алгоритм продовжує роботу.
На відміну від універсальних алгоритмів вузькоспеціалізований алгоритм видалення невидимих граней опуклих тел дозволяє робити обчислення набагато швидше. Він працює для центральної перспективної проекції. Розглянемо роботу цього алгоритму на прикладі як зображено на рис. 38.
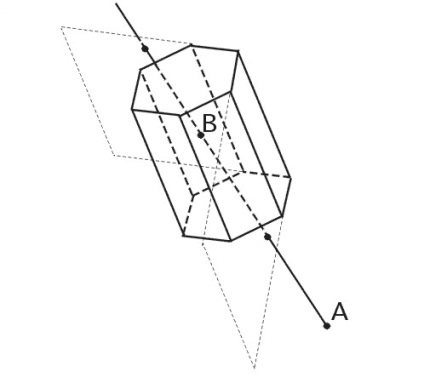
Мал. 38. Перетинання прямої AB з площинами граней призми.
Нехай спостерігач знаходиться в точці A. Виберемо точкуB. яка свідомо є внутрішньою для опуклою фігури, в даному випадку призми. Виберемо деяку грань, про яку ми хочемо дізнатися видима вона з точкіA. або не видима. Побудуємо площину, в якій лежить обрана грань. Знайдемо точку перетину площини і прямої, яка утворена отрезкомAB. Якщо точка перетину прямої і площини лежить всередині отрезкаAB. то робимо висновок, що дана грань видима. Якщо точка перетину знаходиться поза отрезкаAB. то грань не видима. У разі, коли пряма і площина паралельні, вважаємо що грань не видима.