Повернемося до блок-схемі рис. 6. Тема її циклу представлений блоком 4. Роль лічильника циклу грає змінна i, яка повинна в циклі змінюватися від 1 до N. Оскільки крок явно не вказано, то за замовчуванням він мається на увазі рівним 1. Тіло циклу утворюють блоки 5 і 6.
Як видно з рис.7, цикл складається з заголовка і тіла. Всякий цикл обов'язково має свій лічильник.
На рис. 8, де показана структура і параметри заголовка циклу, роль такого лічильника виконує змінна i. Усередині заголовка після лічильника і символу "=" через кому вказує початкове і кінцеве значення лічильника і крок його зміни (на рис. 8 їх роль виконують змінні j, k, l відповідно). Якщо значення кроку l = l, то його можна не вказувати.
Рис.7. Структура циклу. Рис.8. Структура заголовка циклу
Усередині заголовка лічильнику спочатку присвоюється значення i = j. Потім виконується блоки, що утворюють тіло циклу. Обробка блоків всередині циклу проводиться за годинниковою стрілкою. В результаті після першого виконання тіла циклу управління знову передається заголовку. Тут до поточного значення лічильника додасться крок. Тепер, якщо нове значення лічильника не вийшло за свої межі (т. Е. Не побільшало свого кінцевого значення при позитивному кроці або менше кінцевого значення - при негативному кроці), то знову виконується тіло циклу, знову після повернення до заголовку до лічильника додається крок . Так цикл буде виконуватися до тих пір, поки значення лічильника одного разу не вийде за вказаний межа. Як тільки така межа буде подолано, відбудеться вихід з циклу і управління буде передано блоку, який йде відразу за циклом.
Відразу після входу в цикл змінна i прийме початкове значення i = 1. Далі в блоці 5 виконується перевірка позитивності першого елемента масиву Z (т. К. I = 1). Якщо цей елемент дійсно позитивний, то в блоці б він буде доданий до змінної S, після чого виконується повернення до заголовку циклу. Якщо цей елемент не позитивний (т. Е. Нуль або негативний), то буде виконаний перехід відразу до заголовку циклу, минаючи блок підсумовування 6.
На другому колі циклу лічильник i в заголовку збільшиться на 1 і стане рівним 2. Тепер, при новому виконанні тіла циклу, в блоці 5 перевіряється на позитивність другий елемент масиву Z і, якщо він позитивний, то додається в суму і т. Д. Останній раз тіло циклу виконається при i = N. при цьому значенні лічильника перевіряється останній елемент масиву. Нарешті, в заголовку циклу i прийме значення N + 1. Це значення виходить за вказаний межа, отже, відбудеться вихід з циклу і управління перейде блоку 7. У цьому блоці виводиться накопичена сума і алгоритм закінчить роботу.
Нерідко при алгоритмічній вирішенні задачі виникає необхідність створення циклу, що містить в своєму тілі іншої цикл. Такі вкладені одна в одну цикли відносяться до структур вкладених циклів. Порядок вкладеності циклів, коли в тілі внутрішнього циклу містяться інші цикли, може бути досить великим. Цей порядок визначається методом, за допомогою якого досягається рішення поставленого завдання. Так, при обробці одновимірних масивів, як правило, вдається побудувати алгоритмічну схему без вкладення циклів. Однак в ряді випадків при вирішенні таких завдань без вкладених циклів не обійтися.
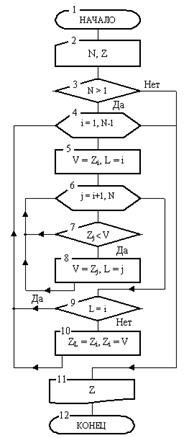
Рис.9. Алгоритм сортування масиву
Відзначимо, що всі вкладені одна в одну цикли, включаючи зовнішній, повинні мати лічильники з різними іменами. Поза цими циклів лічильники можуть бути використані як звичайні змінні або як лічильники інших циклів.
Приклад 1. Розглянемо задачу сортування одновимірного масиву Z довжини N. Відсортувати масив - значить розташувати його елементи в порядку зростання або убування.
Опишемо метод сортування масиву в порядку зростання. Спочатку виконується прохід по масиву з метою визначення в ньому найменшого елемента. Потім проводиться перестановка цього елемента з першим. Далі відбувається другий прохід по масиву, починаючи з другого елементу. Знайдений найменший елемент переставляється з другим і т. Д. Після (N-1) -го проходу з виконанням названих операцій масив виявиться відсортованих.
Блок-схема цього алгоритму сортування показана на рис. 9. Вона включає 12 блоків. Після початку роботи в блоці 2 змінна N і масив Z заповнюються константами. Потім в блоці 3 перевіряється умова про те, чи потрібно сортувати масив.
Це зводиться до встановлення факту наявності в масиві декількох елементів, т. К. Масив з одного елемента завжди впорядкований. Якщо цей факт встановлений, то алгоритм приступає до сортування. Процедура сортування виконується в циклі, що об'єднує блоки 4-10. У тілі цього циклу міститься інший цикл, який утворений блоками 6-8. Його призначення стане ясно з подальшого розбору алгоритму.
Після входу в зовнішній цикл його лічильник i прийме значення 1, що в рамках нашого методу має на увазі перший прохід по масиву.
Далі будуть виконані блоки 5-10, складові тіло зовнішнього циклу. У блоці 5 розміщені дві допоміжні змінні V і L. Перша з них призначена для фіксування найменшого елемента, а друга - для запам'ятовування його індексу. Так як i = 1, то при першому проході в блоці 5 V прийме значення першого елемента, а L значення 1. Потім у внутрішньому циклі, утвореному блоками 6-8, де його лічильник j буде змінюватися від 2 до N, послідовно проводиться порівняння відповідних елементів масиву Z зі значенням змінної V. При цьому всякий раз, як буде знайдений менший ніж v елемент, значення V буде замінено на значення цього елемента, а в змінної L буде зафіксований його індекс. Зрозуміло, що після виконання внутрішнього циклу в змінної V міститиметься значення, рівне найменшому елементу, а в L - індекс цього елемента. У блоці 9 далі перевіряється, чи не є найменший елемент першим елементом масиву. Якщо це не так, то в блоці 10 на місце найменшого елемента (його номер L) запишеться перший (т. К. При першому проході L = 1), а на місце першого елемента - найменший (він дорівнює V). Після цього відбудеться повернення управління до заголовку зовнішнього циклу блоку 4. У ньому значення лічильника стане рівним i = 2.
Потім знову виконується його тіло, але вже для нового значення лічильника i. Тепер за допомогою блоків 5-10 відшукується найменший елемент масиву, починаючи з номера 2. Потім в блоках 9-10 він посяде друге місце в масиві і т. Д. Коли тіло зовнішнього циклу виконається (N-1), раз масив буде відсортований.
У блоці 12 відсортований масив буде виведений і в блоці 13 алгоритм закінчить роботу.
Алгоритми зі структурами вкладених циклів часто використовують при вирішенні задач обробки двовимірних масивів. У таких алгоритмах лічильники циклів використовуються для маніпуляції з індексами масивів.
Приклад 2. Дан двовимірний квадратний масив Z, що складається з N рядків і N стовпців. Необхідно знайти середнє арифметичне S його негативних елементів і замінити позитивні елементи побічної діагоналі масиву середнім арифметичним S.
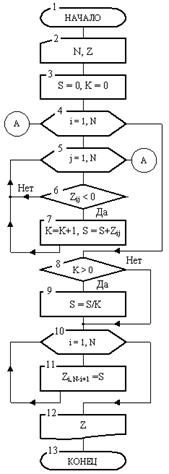
Мал. 10. Блок-схема алгоритму
Блок-схема алгоритму показана на рис. 10. Вона складається з 13 блоків. У блоці 2 змінна N і весь масив Z заповнюються константами. У блоці 3 робочі змінні S і К отримує значення нуль. Мінлива S спочатку буде грати роль сумматора негативних елементів масиву, потім після накопичення суми вона прийме значення середнього арифметичного. Мінлива До потрібна для підрахунку кількості негативних елементів масиву.
У блоках 4-7 виконується накопичення суми негативних елементів масиву.
Ці блоки утворює два вкладених циклу, причому внутрішній цикл з лічильником j є тілом зовнішнього циклу з лічильником i. Проаналізуємо роботу цієї структури.
Після входу в зовнішній цикл в блоці 4, змінна i прийме значення i = 1. Далі буде виконано його тіло (блоки 5-7), яке, в свою чергу, також є циклом. Після входу у внутрішній цикл в блоці 5, змінна j прийме значення j = 1. Потім в блоці 6 перевіряється на негативність елемент масиву Z, розташований в першому рядку і першому стовпці, т. К. I = 1 і j = 1.
Якщо він виявиться негативним, то в блоці 7 змінна До збільшиться на 1, а до S додається значення цього елемента. Після цього виконується повернення до блоку 5, т. Е. До заголовку внутрішнього циклу. Тут j збільшиться на 1, стане рівною j = 2 і управління перейде до блоку 6. У ньому перевіряється елемент, що стоїть все в тій же першому рядку, але в другому стовпці (i = 1, j = 2). Якщо він виявиться негативним, то До знову збільшиться на 1, а до накопиченого до цього часу S додається значення цього елемента і т.д. Коли повністю виконається внутрішній цикл, т. Е. Змінна j "пробіжить" від 1 до N, в змінну S накопичиться сума всіх негативних елементів першого рядка масиву, а в К - їх кількість. Тепер управління передається до блоку 4 заголовка зовнішнього циклу, де i стане рівною i = 2. Знову буде відпрацьовано його тіло, т. Е. Цикл 5-7. При цьому буде знайдена вже сума негативних елементів перших двох рядків масиву, а в До збережеться кількість цих елементів. Коли виконається весь зовнішній цикл, в S буде константа, яка дорівнює сумі негативних елементів всього масиву, а в К - їх кількість. Тепер управління перейде до блоку 8. Якщо виявиться, що в масиві є негативні елементи (К> 0), то в блоці 9 обчислюється середнє арифметичне як відношення суми елементів до їх кількості. Результат поміщається а ту ж змінну S. Відзначимо, що якби блок 8 перевірки був відсутній, то при К = 0 (в масиві немає жодного негативного елементу) в блоці 9 через ділення на нуль виникла б помилка. Ця помилка спричинила б аварійне завершення обчислень до закінчення роботи алгоритму.
Далі виконується блоки 10-11, які також утворює цикл. У ньому проводиться заміна елементів побічної діагоналі на середнє арифметичне S (побічної діагоналлю є прямолінійна ланцюжок осередків в діапазоні від нижнього лівого кута до верхнього правого кута масиву). Зверніть увагу, на те що змінна i, яка використовувалася раніше, з метою економії пам'яті застосовується знову.
Простежимо роботу цього циклу. Після входу в блок 10 лічильник прийме значення i = 1. Потім в блоці 11 при цьому значенні буде вирахувано індекс стовпця елемента N - 1 + i = N. Таким чином, елемент з індексами (1, N) стане рівним S. На другому колі циклу i збільшиться на 1 і стане i = 2. Неважко бачити, що тепер елемент (2, N-1) стане рівним S і т. д. на останньому колі циклу елемент (N, 1) отримає значення S, що завершить зміну значень всіх елементів побічної діагоналі на середнє арифметичне S.
Нарешті, в блоці 12 змінений масив буде виведений і в блоці 13 алгоритм закінчить роботу.