Щоб спростити вираз arcsin (x) + arcsin (-x) або arctg (x) + arctg (-x), досить пам'ятати лише одне властивість арксинуса (арктангенса).
arcsin (-x) = - arcsin (x), arctg (-x) = - arctg (x). Тому
arcsin (x) + arcsin (-x) = arcsin (x) -arcsin (x) = 0,
arctg (-x) + arctg (x) = 0.
tg (arcsin (x) + arcsin (-x)) = tg 0 = 0,
sin (arcsin (x) + arcsin (-x)) = sin 0 = 0,
cos (arcsin (x) + arcsin (-x)) = cos 0 = 1,
tg (arctg (-x) + arctg (x)) = tg 0 = 0,
sin (arctg (-x) + arctg (x)) = sin 0 = 0,
cos (arctg (-x) + arctg (x)) = cos 0 = 1.
Якщо потрібно побудувати графік функції y = arcsin (-x) + arcsin (x), рішення починаємо з знаходження області визначення.
Область визначення цієї функції збігається з областю визначення функції y = arcsin (x):
Таким чином, графік функції y = arcsin (-x) + arcsin (x) зводиться до графіка лінійної функції y = 0 і являє собою відрізок, що лежить на осі ох з кінцями в точках х = -1 і х = 1:
Графіки функцій y = sin (arcsin (-x) + arcsin (x)) і y = tg (arcsin (-x) + arcsin (x)) також представляють собою відрізки від x = -1 до x = 1, що лежать на осі ox. Хоча при знаходженні області визначення другої функції враховуємо, що тангенс не визначений в точках виду
жодна з таких точок не належить відрізку від -1 до 1.
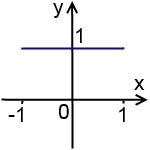
Графік функції y = cos (arcsin (-x) + arcsin (x)) - відрізок прямої y = 1 з кінцями в x = -1 і x = 1:
arccos (-x) = П-arccos (x), arcctg (-x) = П-arcctg (x). Тому
arccos (-x) + arccos (x) = П-arccos (x) + arccos (x) = П,
arcctg (-x) + arcctg (x) = П-arcctg (x) + arcctg (x) = П.
sin (arccos (-x) + arccos (x)) = sin П = 0,
cos (arccos (-x) + arccos (x)) = cos П = -1,
tg (arccos (-x) + arccos (x)) = tg П = 0,
sin (arcctg (-x) + arcctg (x)) = sin П = 0,
cos (arcctg (-x) + arcctg (x)) = cos П = -1,
tg (arcctg (-x) + arcctg (x)) = tg П = 0.
Область визначення функції y = arccos (-x) + arccos (x) -
Графік функції є відрізок від x = -1 до x = 1 - частина прямої y = П:
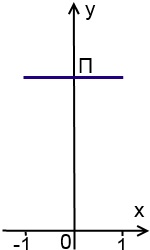
y = arccos (-x) + arccos (x)
Графік функції y = arcctg (-x) + arcctg (x) - пряма y = П (область визначення арккотангенса - вся числова пряма):
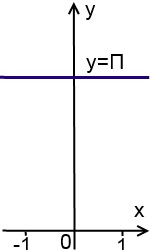
Графік функції y = tg (arctg (x) + arctg (-x)) - пряма y = 0 (тобто вісь ox) з виколотими точками x = П / 2 + Пn, де n - цілі числа:
y = tg (arctg (x) + arctg (-x))
y = tg (arcctg (x) + arcctg (-x))
Графік функції y = tg (arcctg (x) + arcctg (-x)) - така ж пряма.
Графіки функцій y = sin (arctg (x) + arctg (-x)) і y = sin (arcctg (x) + arcctg (-x)) представляють собою пряму y = 0 (тобто вісь ox).
Графік функції y = ctg (arcctg (x) + arcctg (-x)) - пряма y = 0 з виколотими точками