Способи завдання графів:
Завдання графа за допомогою матриці інцидентності
nm - де n кількість вершин графа, m - кількість ребер графа. По вертикалі і горизонталі вказуються вершини і ребра, а на перетині i-рядка і j-стовпця, якщо ребро i інцидентне вершині j ставимо 1 і 0 в іншому випадку.
У разі орграфа
В петлі присвоюється будь-яке інше число. (Найчастіше 2)
Списком ребер графа
Список ребер графа представл. стовпцем. У лівому стовпчику перераховується все ребра, а в правому інцідентние йому вершини, причому для n-графа порядок написання вершин довільний, а для ор-графа першим стоїть номер початку дуги.
Якщо граф має ізольовані вершини, то вони будуть розміщені в кінець списку.
Матриця суміжності - це квадратна матриця розміру, гдеn - кількість вершин графа.
У разі n-графа проставляється число ребер з'єднують ці дві вершини.
У разі ор-графа проставляється кількість дуг мають початок в вершині і кінець в вершині.
Визначення 2.21. Матрицею суміжності кінцевого графа G з p вершинами називається матриця A (G) = || aij || (I, j = 1, 2, ..., p), в якій якщо суміжні вершини то ставимо 1, інакше 0.
42. Дії над графами.
Граф H будемо називати частиною графа G (), якщо мн-воV (H) і мн-во ребер E (H) міститься у відповідних мн-вах для графа G: і.
Граф H називається суграфом графа G, якщо він є частиною графа G і кількість вершин графа H одно кількістю вершин графа G, т.е.V (H) = V (G).
Граф G () назив.подграфом графа G (V), якщо граф G () містить всі ребра, які інцидентні вершинам з мн-ва.
Визначимо деякі операції на графах:
Видалення або додавання ребра.
Видалення вершини. З безлічі вершин видаляємо обрану вершину, а з безлічі ребер все інцідентние їй ребра.
Стягування ребра. Ототожнюємо (стягуємо) вершини інцидентні заданої ребру.
Додавання вершини (розбиття ребра). Виберемо деякий ребро (u, v) з безлічі ребер і видалимо його. У безліч вершин додамо нову вершину w, а в безліч ребер нові ребра (u, w) і (w, v).
Доповнення частини H графа G явл. графом задовольняє слід. умовами:
43. Орієнтовані і неорієнтовані графи.
ГрафомG називається сукупність 2-х множин (V, E), де V - безліч вершин графа, а Е - безліч ребер графа. Між вершинами і ребрами графа G встановлюють відношення інцидентності. Вважають, що ребро інцидентне вершин ,, якщо воно з'єднує ці 2-е вершини. При цьому вершини, називаютсясмежнимі. Ставлення инцидентности є найголовнішим елементом графа, тому що вказує спосіб об'єднання множин V і E в єдиний об'єкт. Якщо ребро, що з'єднує 2-е вершини, направлено від однієї вершини до іншої, то воно називаетсяоріентірованним або дугою і графічно зображується стрілками, спрямованими від початку до кінця. Граф, що містить дуги називається орієнтованим або Орграф. Граф, який не містить жодної дуги (який містить лише ребра) називається неорієнтованим або н-графом.
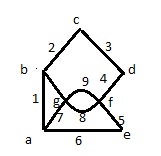
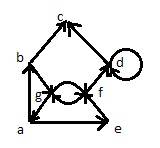
Н-ГРАФ (Рис.1) ОР-ГРАФ (Рис.2)
Ребра, інцідентние однієї і тієї ж парі вершин називаються кратними (на рис.1 це ребра 8 і 9).