
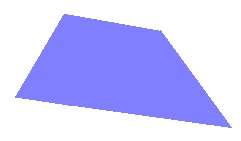
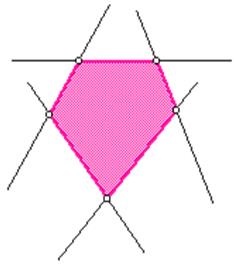
2 Опуклі і неопуклі багатокутники Багатокутник називається опуклим, якщо він лежить по одну сторону від кожної прямої, що проходить через дві його сусідні вершини.
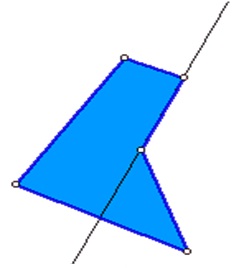
3 Опуклі і неопуклі багатокутники Багатокутник називається неопуклого, якщо існує пряма, яка містить його сторону, яка розбиває його на дві частини.
if ($ this-> show_pages_images $ Page_num doc [ 'images_node_id'])
4 Властивості опуклих багатокутників 1 0 Відрізок, що з'єднує будь-які дві точки опуклого плоского багатокутника (зокрема, будь-яка його діагональ), міститься в цьому багатокутнику. 2 0 Опуклий плоский багатокутник розбивається на трикутники усіма діагоналями, проведеними з однієї (будь-який) його вершини. 3 0 Сума кутів опуклого n-кутника дорівнює 180 (n 2).
5 Види плоских багатокутників
6 Види опуклих багатокутників
7 Види неопуклих багатокутників
8 Види зірчастих многокутників
9 Види плоских багатокутників

10 Правильні багатокутники
11 Правильні багатокутники Опуклий багатокутник називається правильним, якщо у нього всі кути рівні і всі сторони рівні.
12 ПІФАГОРІЙЦІ Вчення про правильні багатокутники зародилося в школі ПІФАГОРА; крім того, піфагорійці розглянули питання покриття площині правильними багатокутниками. Піфагор Самоський (рр. До н. Е.) Давньогрецький філософ і математик.

13 АРХИМЕД Для обчислення площі кола і довжини окружності використовували побудова правильних вписаних і описаних багатокутників. Архим д (рр. До н.е.) давньогрецький математик, фізик, інженер. АРХИМЕД при роботі з правильним 96-кутником вивів значення числа π.
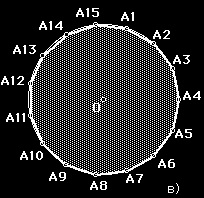

14 Евкліда Евклі д (бл. 300 р. До н.е..) Давньогрецький математик. Вперше описав побудова правильних 3, 4, 5, 6 - кутників, побудував правильний 15 кутник.

16 ЕПОХА ВІДРОДЖЕННЯ Розвиток готичного стилю і широке застосування вітражів в будівництві соборів також змусило повернутися до завдань побудови правильних багатокутників.
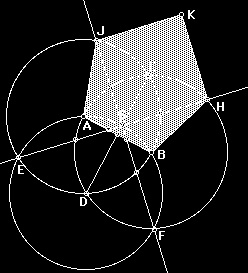

17 АЛЬБРЕХТ ДЮРЕР- «ПІВНІЧНИЙ ЛЕОНАРДО» Німецький художник Альбрехт Дюрер (рр.) Здійснив нове побудова правильного п'ятикутника, передавши нащадкам середньовічний спосіб побудови постійним розчином циркуля.


18 АЛЬБРЕХТ ДЮРЕР- «ПІВНІЧНИЙ ЛЕОНАРДО» А.Дюрер займався фортифікацією, розробляючи системи оборонних споруд; вирішив задачу побудови правильного восьмикутника; розробив принципи креслення художньо виконаних букв.

19 ВЕЛИКИЙ Леонардо да Вінчі Італійський художник і вчений Леона РДО ді сер П'є ро да Ві нчі (рр.) Займаючись побудовами, встановив співвідношення між стороною n-кутника і апофемой; не залишив без уваги і розробку перших друкарських шрифтів; залучали його увагу і орнаменти.

20 Леонардо да Вінчі Для свого друга італійського математика Луки Пачолі (рр.) Леонардо, глибоко цікавиться пропорціями, створив ілюстрації багатогранників, гранями яких є правильні багатокутники.

22 КАРЛ ФРИДРИХ Гаус Довів можливість побудови правильного 17- кутника. Після цього 19-річний юнак вирішив зайнятися математикою, а не філологією.
23 Вписані і описані многокутники Опуклий багатокутник називається вписаним в коло, якщо всі його вершини належать цієї окружності. Кутника можна називається описаним близько кола, якщо всі його сторони стосуються цієї окружності.

24 Властивості правильних багатокутників 1 0 Правильний багатокутник є вписаною в коло і описаних близько кола, при цьому центри цих кіл збігаються. 2 0 Центр правильного багатокутника збігається з центрами вписаного і описаного кіл. 3 0 Сторона an правильного n-кутника пов'язана з радіусом R описаного кола формулою an = 2rsin180 0 n. 4 0 Периметри правильних n-кутників відносяться як радіуси описаних кіл.
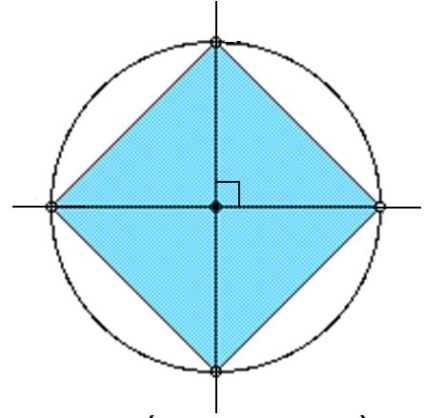
25 Побудова правильних багатокутників Побудова правильного трикутника Побудова правильного шестикутника Побудова правильного чотирикутника (квадрата)
26 Побудова правильних багатокутників Чи кожен правильний багатокутник можна побудувати циркулем і лінійкою? Якщо побудований якийсь правильний n-кутник, то за допомогою циркуля і лінійки можна побудувати правильний 2n-кутник. Наприклад, побудувавши циркулем і лінійкою правильний трикутник, можна побудувати за допомогою циркуля і лінійки правильні 6-кутник, 12-кутник, 24-кутник, 48-кутник і т.д.
27 Побудова правильних багатокутників
28 Побудова правильних багатокутників
29 Побудова правильних У разі, коли правильний багатокутник можна побудувати циркулем і лінійкою, користуються наближеними методами побудови (для практичних цілей). Наприклад, наближене побудова правильного п'ятикутника можна виконати так: AD діаметр, AB = BC = CD; AMNKP шуканий п'ятикутник. багатокутників
31 ПЕНТАГОН Будівля військового відомства США має форму пентаграми і отримало назву «Пентагон», що означає правильний п'ятикутник.
32 Напівправильні багатокутники Напівправильні будемо називати такі опуклі багатокутники: а) рівнокутні, у яких сторони рівні через одну; б) рівносторонній, у яких кути рівні через один.
33 Приклади напівправильних багатокутників Рівнокутні-напівправильні: рівносторонній-напівправильні:
34 Властивості напівправильних багатокутників 1 0. Напівправильні багатокутники мають парне число вершин Близько будь-якого равноугольнополуправільного багатокутника можна описати коло, і притому тільки одну У будь-рівносторонньо-Напівправильні багатокутник можна вписати коло, і притому тільки одну Протилежні сторони равноугольнополуправільного багатокутника паралельні.

35 Зірчасті багатокутники Серед зірчастих многокутників виділяють правильні і напівправильні, які в свою чергу діляться на равноугольнополуправільние і равностороннеполуправільние зірчасті багатокутники.
36 Приклади правильних зірчастих многокутників
37 Приклади напівправильних зірчастих многокутників Рівнокутні-Напівправильні зірчастий багатокутник рівносторонній-Напівправильні зірчастий багатокутник
38 Побудова правильних зірчастих многокутників Якщо сторони правильного n-кутника, де n> 4, продовжити до перетину з продовженням іншого боку, то можна отримати правильний зірчастий (самопересекающийся) n- кутник. Приклад побудови правильного зірчастого шестикутника
39 Правильні багатокутники в природі
40 Правильні багатокутники в природі
41 Правильні багатокутники в природі
42 Правильні багатокутники в природі
43 Паркети з правильних багатокутників

44 пентаграма Найбільший інтерес викликає досконала геометрична фігура, яка отримала назву пентаграми або пентакль. Пентаграма служила таємним знаком пифагорейского братства і була обрана ними як символ життя і здоров'я. Згідно з легендою, один піфагорієць захворів на чужині і не міг перед смертю розплатитися з доглядають за ним господарем будинку. Останній намалював на стіні свого будинку зірчастий п'ятикутник. Побачивши через кілька років цей знак, інший мандрівний піфагорієць поцікавився про те, що сталося у господаря і щедро його винагородив.
45 пентаграма Пентаграмма пропорційна і, отже, красива. Не випадково і сьогодні п'ятикутна зірка майорить на прапорах чи не половини країн світу. Буркіна Фасо Венесуела Гвінея - Бісау Гена В'єтнам Гондурас Гренада Джібуті Домініка Зімбабве Ірак Ємен
46 пентаграма Камерун Китай Коморські острови Корейська народна демокр-ая р - ка Куба Ліберія Мавританія Мікронезія Мозамбік Нова Зеландія Пакистан Папуа Нова Гвінея Настільки надзвичайно пропорційне будова пентаграми, краса еѐ внутрішнього математичного змісту є основою еѐ зовнішньої краси.
47 Правильні і зірчасті багатокутники в декоратівнопрікладном мистецтві Візерунок «Зірка» Візерунок «Ромашка»
48 Правильні і зірчасті багатокутники в декоратівнопрікладном мистецтві Візерунок «восьмикутний зірка» Візерунок «Шахматка» Візерунок «Сонечко» Серветка «Квітка»


49 Правильні і зірчасті багатокутники у виробах удмуртского декоративно-прикладного мистецтва
50 Правильні і зірчасті багатокутники у виробах удмуртского декоративно-прикладного мистецтва

51 Правильні і зірчасті багатокутники у виробах удмуртского декоративно-прикладного мистецтва
52 Дякую за увагу!