OpenMP - не просто бібліотека паралельного програмування, а й стандарт, офіційно підтримуваний для мов Сі, C ++ і Fortran (а неофіційно і для інших мов, Free Pascal, наприклад [1]). Працює OpenMP тільки на архітектурі із загальною пам'яттю.
Бібліотека OpenMP задумана так, що програміст спочатку може написати послідовну програму. налагодити її (адже налагоджувати паралельну програму дуже важко), а потім, поступово распараллеливать. доповнюючи директивами OpenMP.
Не секрет, що більшу частину часу виконання, програми проводять всередині циклів. Напевно тому, в OpenMP є спеціальна директива паралельного циклу, їй і присвячена більша частина статті.
У статті розглянуті 2 приклади розпаралелювання:
- обчислення суми елементів масиву;
- обчислення інтеграла методом прямокутників.
Всі приклади статті написані на С ++. використовувався компілятор gcc (але можна використовувати і інші, відрізнятися будуть тільки ключі. передаються компілятору). Для підтримки OpenMP. gcc повинен прийняти ключ -fopenmp.
1 Обчислення суми елементів масиву
Як зазначалося вище, OpenMP дозволяє распараллеливать нашу програму поступово, а спочатку можна написати послідовну програму і налагодити, що ми і зробили:
Функція гранично проста і ми бачимо в ній цикл, ітерації якого, можна було б розподілити по окремих потокам. При використанні інших бібліотек нам би довелося розподіляти ітерації вручну, при цьому, кожен потік обчислював би частину суми, а в кінці, потоки повинні б були якось синхронізуватися і об'єднати результати.
OpenMP нам, також, дозволяє розподіляти роботу вручну, але частіше за все це не потрібно, адже є більш зручні засоби.
У третьому рядку директива parallel задає паралельну область. яка поміщається всередину фігурних дужок. На початку цього області створюються потоки, кількість яких можна задати за допомогою опції num_threads (в прикладі область виконується в двох потоках).
Потік може використовувати як локальні змінні. так і колективні. Спільні змінні (shared) є загальними для всіх потоків, очевидно, з ними треба дуже обережно працювати (якщо хоч один потік змінює значення такої змінної - всі інші повинні чекати - це можна організувати засобами OMP). Всі константи є розділяються - в нашому прикладі, що розділяються є змінні "a" і "n".
Потік може містити набір локальних змінних (опції private і firstprivate), для яких породжуються копії в кожному потоці. Для змінних, оголошених в списку private початкове значення не визначене, для firstprivate - береться з головного потоку. Всі змінні, оголошені всередині паралельної області є локальними (змінна "i" в нашому прикладі).
Опція reduction. також, задає локальну змінну (sum), а також, операцію, яка буде виконана над локальними змінними при виході з паралельної області ( "+"). Початкове значення локальних змінних, в цьому випадку, визначається типом операції (для адитивних операцій - нуль. Для мультиплікативних - одиниця).
У п'ятому рядку прикладу задається початок паралельного циклу. Ітерації циклу, наступного за відповідною директивою будуть розподілені між потоками.
Директива for має безліч опцій, докладніше про які можна прочитати в товстих підручниках. Всередині циклу можна задати опції private і firstprivate. але крім того, ряд нових. Наприклад schedule визначає спосіб розподілу ітерацій між потоками, а nowait - прибирає неявну бар'єрну синхронізацію, яка за замовчуванням стоїть в кінці циклу.
В кінці статті додається архів з вихідним кодом прикладу. Можна перевірити що паралельна програма працює значно швидше.
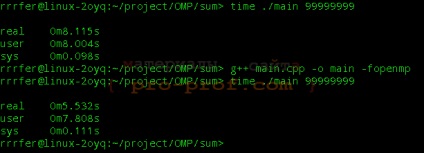
Мал. 1 розпаралелювання OMP
Сума елементів масиву вважається дуже швидко, тому щоб отримати результати, показані на малюнку, довелося запустити нашу функцію 10 разів. Велику частину часу роботи програми займає заповнення масиву випадковими числами, яке виконується в одному потоці (через це результати трохи змазані). Однак, не ледачий читач може без праці распараллелить заповнення масиву :).
2 Обчислення інтеграла методом прямокутників
2.1 Визнач кількість прямокутників
У статті використовується метод лівих прямокутників, суть якого зводиться до того, що область між графіком інтегрованої функції і віссю абсцис розбивається на задану кількість прямокутників. Для кожного прямокутника обчислюється площа, сума площ - і є результат. Термін "ліві прямокутники" означає, що лівий верхній кут кожного прямокутника лежить безпосередньо на інтегрованої функції.
На С ++ описаний алгоритм може бути виражений наступним чином (відразу наведено паралельний варіант, тому що немає нічого нового):
У наведеному коді немає нічого принципово нового, можна відзначити лише те, що при описі паралельної секції не ставить кількість потоків - в цьому випадку воно буде визначатися значенням змінної середовища OMP_NUM_THREADS. Код пояснює метод прямокутників (для тих, хто забув) - далі ми подивимося на інші варіанти реалізації цього методу. Крім того, на цьому простому прикладі можна подивитися на деградацію точності при збільшенні кількості прямокутників.
Мал. 2 деградація точності при великій кількості прямокутників
Як аргумент програма на рис. 2 приймає кількість прямокутників, інтегрується функція x * x на інтервалі [-1, 1]. точне значення інтеграла 2/3. Чим більше прямокутників на обмеженому інтервалі - тим менше кожен прямокутник, отже, прямокутники "щільніше прилягають до графіка" і точність повинна зростати. Точність дійсно підвищується, ми бачимо це при збільшенні кількості прямокутників з 10 до 100. однак, при дуже великій їх кількості точність різко падає. OpenMP тут виявляється і ні до чого (зверніть увагу, при компіляції не використовувалася ключ -fopenmp).
У наведеному прикладі точність падає тому, що дуже маленьке значення кроку (h) множиться на дуже велике значення лічильника (i). У молодших розрядах кроку знаходиться сміття, цього не можна уникнути. Це сміття ми і обробляємо замість потрібних нам даних. Ми спостерігаємо помилку, про яку і не здогадується комп'ютер, програма в цьому випадку не викине винятків, особливо важко визначити причину таких помилок в паралельних програмах.
OpenMP тут начебто і ні до чого, але виявляється так, що на точність може впливати кількість працюючих потоків і порядок обчислення. Читач може переконатися в цьому, наприклад послідовно обчисливши суму ряду 1 / (x * x) спочатку при зміні x від 1 до 100000000. а потім, в зворотному порядку. Результати обчислень будуть відрізнятися, і обчислення в зворотному порядку дає більш точний результат (якщо з якогось дива і дуже цікаво - повідомте, я напишу статтю по цій темі). OpenMP не гарантує певний порядок обчислень, тому і може з'являтися несподівана похибка, на це багато разів вказується в деяких джерелах [2].
2.2 Задана точність інтегрування
Так чи інакше, в попередньому прикладі у нас вийшло без особливих зусиль распараллелить послідовну програму (як і замислювалося розробниками OpenMP). Може здатися, що так буде завжди, але це не так. Чуть-чуть змінимо умову попередньої задачі - тепер нам задана точність, якої треба досягти, а не кількість прямокутників.
Програма буде поступово дробити крок і вважати з ним суму площ прямокутників до тих пір, поки різниця сумарної площі на поточному кроці і попередньому не опиниться менше точності. Висловити цю ідею в коді можна наступним чином:
Це, очевидно, не найкращий код, але він приведений, щоб показати, що OpenMP не здатна распараллелить програму в деяких випадках (таких як цей). Для розподілу ітерацій між потоками, OpenMP повинна мати можливість визначити кількість цих ітерацій, але це неможливо для прикладу лістинг 4.
Зовнішній цикл виконується до тих пір, поки не буде досягнута задана точність, і немає ніякої можливості визначити скільки ітерацій потрібно - це в більшій мірі залежить від властивостей інтегрованої функції, яка може бути будь-хто.
Здається, що внутрішній цикл можна распараллелить, але це не так. Кількість ітерацій можна визначити точно, тому що в якості лічильника використовується змінна подрібнена типу. а в ній може накопичуватися похибка (як показано вище). У OpenMP паралельний цикл повинен мати цілочисельний лічильник.
Однак, це не означає, що OpenMP не може распараллелить вирішення такого завдання, проте код повинен бути написаний певним чином. Те, що кількість ітерацій внутрішнього циклу не можна визначити, говорить про те, що це поганий код, незалежно від того, буде він працювати послідовно або паралельно.
Для використання OpenMP в цьому прикладі досить визначити заздалегідь кількість ітерацій внутрішнього циклу і використовувати в ньому цілочисельний лічильник:
Висновок з лістинг 4 і 5 повинен бути такий, що хоч OpenMP і задуманий як засіб поступового розпаралелювання послідовних програм, але програма для цього повинна писатися певним чином. Через описаних вище проблем, функція лістинг 5 може працювати невірно при запиті дуже високої точності, але звинувачувати в цьому OpenMP можна.