// Якщо так, то зробити приріст змінної count
if (t-> Left () == NULL t-> Right () == NULL)
Функція Depth використовує зворотний метод проходження для обчислення глибини бінарного дерева. У кожному вузлі обчислюється глибина його лівого і правого піддерев. Підсумкова глибина на одиницю більше максимальної глибини піддерев.
// Ця функція використовує зворотний метод проходження
// для обчислення глибини лівого і правого піддерев
// вузла і повертає результуючий значення глибини,
// рівне 1 + max (depthLeft, depthRight).
// Глибина порожнього дерева дорівнює -1
template
void Depth (TreeNode
int depthLeft, depthRight, depthval;
depthval = 1 + (depthLeft> depthRight depthLeft. depthRight);
b = GetTreeNode ( 'B', NULL, d);
c = GetTreeNode ( 'C', e, NULL);
a = GetTreeNode ( 'A', b, c);
Спочатку ми створюємо сина D, який потім приєднується до свого батька B при створенні вузла. Створюється вузол E і приєднується до свого батька C під час народження (або створення) останнього. Нарешті, створюється корінь і приєднується до своїх синів B і C.
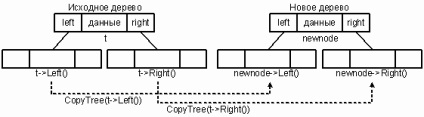
Алгоритм копіювання дерева починає працювати з кореня і в першу чергу будує ліве піддерево вузла, а потім - праве його поддерево. Тільки після цього створюється новий вузол. Той же рекурсивний процес повторюється для кожного вузла. Відповідно вузлу t вихідного дерева створюється новий вузол з покажчиками newlptr і newrptr.
При зворотному методі проходження сини відвідуються перед їх батьками. В результаті в новому дереві створюються піддерева, що відповідають t-> Left () і t-> Right (). Сини приєднуються до своїх батьків в момент створення останніх.
// створити батька і приєднати до нього його синів
newnode = GetTreeNode (t-> data, newlptr, newrptr);
Суть відвідування вузла t в початковому дереві полягає в створенні нового вузла на дереві-дублікаті.
TreeNode
MakeCharTree (root1, 0); // root1 вказує на Tree_0
Пройти нащадків вузла A, починаючи з лівого піддерева (вузла B і далі до вузла D, який є правою піддерево вузла B). Створити новий вузол з даними, рівними D, і лівим і правим покажчиками, рівними NULL.
Сини вузла B пройдені. Створити новий вузол з даними, рівними B, лівим покажчиком, рівним NULL, і правим покажчиком, що вказує на копію вузла D.
Оскільки ліве піддерево вузла A пройдено, почати проходження його правого піддерева і дійти до вузла E. Створити новий вузол з даними з вузла E і полями покажчиків, рівними NULL.
Після обробки E перейти до його батьків і створити новий вузол з даними з C. У полі правого покажчика помістити NULL, а лівому покажчику привласнити посилання на копію дочірнього вузла E.
// Створити дублікат дерева t і повернути корінь нового дерева
template
// Змінна newnode вказує на новий вузол, який створюється
// за допомогою виклику GetTreeNode і приєднується
// надалі до нового дереву.
// вузла і передаються в якості параметрів в GetTreeNode
TreeNode
// Зупинити рекурсивне проходження при досягненні
// вузлів дерева t. в кожному вузлі цього дерева функція
// створюється його копія. В іншому випадку повертається
// і підвішує до нього копії синів.
if (t-> Left ()! = NULL)
if (t-> Right ()! = NULL)
// побудувати нове дерево від низу до верху, спочатку створюючи
// двох синів, а потім їх батьків
newnode = GetTreeNode (t-> data, newlptr, newrptr);
// повернути покажчик на новостворене дерево
Коли в додатку використовується така динамічна структура, як дерево, відповідальність за звільнення займаної пам'яті лягає на програміста. Розробимо функцію DeleteTree, в якій застосовується зворотний метод проходження бінарного дерева. Використання зворотного методу проходження гарантує, що ми відвідаємо всіх синів батьківського вузла, перш ніж видалимо його. Операція відвідування полягає у виклику функції FreeTreeNode, що видаляє вузол.
// Використовувати зворотний алгоритм для проходження вузлів дерева
// і видалити кожен вузол при його відвідуванні
template
void DeleteTree (TreeNode
Розробимо також функцію ClearTree, яка видаляє всі вузли дерева і скидає корінь. Функція викликає DeleteTree для видалення вузлів дерева і привласнює покажчику на корінь значення NULL.
// Викликати функцію DeleteTree для видалення вузлів дерева.
// Потім скинути покажчик на його корінь в NULL
template
void ClearTree (TreeNode
t = NULL; // тепер корінь порожній
Бінарні дерева пошуку
Звичайне бінарне дерево може містити велику колекцію даних і все ж забезпечувати швидкий пошук, додавання або видалення елементів. Одним з найбільш важливих додатків дерев є побудова класів колекцій. Для лінійних структур складність алгоритму, що реалізує послідовний пошук дорівнює O (N), що неефективно для великих колекцій. У загальному випадку деревовидні структури забезпечують значно більшу продуктивність, так як шлях до будь-яких даних не перевищує глибини дерева. Ефективність пошуку максимальна при закінченому бінарному дереві і становить O (log2 N). Наприклад, в списку з 10000 елементів передбачуване число порівнянь при послідовному пошуку одно 5000. Пошук же на закінченому дереві зажадав би не більше 14 порівнянь. Бінарне дерево представляє великі потенційні можливості в якості структури зберігання списку.
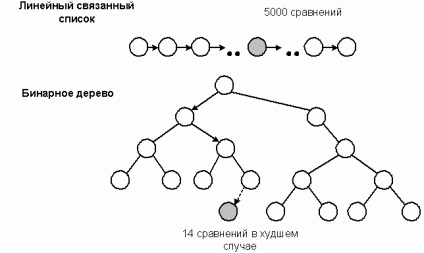
Щоб запам'ятати елементи у вигляді дерева з метою ефективного доступу, ми повинні розробити пошукову структуру, яка вказує шлях до елементу. Ця структура, яка називається бінарним деревом пошуку (binary search tree), впорядковує елементи за допомогою оператора відносини "<". Чтобы сравнить узлы дерева, мы подразумеваем, что часть или все поле данных определено в качестве ключа и оператор "<" сравнивает ключи, когда добавляет элемент. Бинарное дерево поиска строится по следующему правилу:
Для кожного вузла значення даних в лівому поддереве менше, ніж в цьому вузлі, а в правому піддереві - більше або рівні.
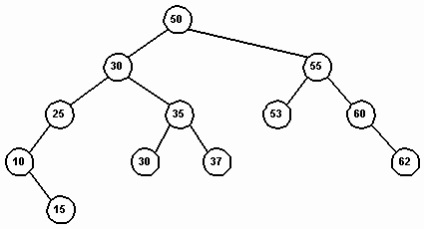
Мал. 10. Бінарне дерево пошуку
На Рис. 10 показаний приклад бінарного пошукового дерева. Це дерево називається пошуковим тому, що в пошуках деякого елемента (ключа) ми можемо йти лише по цілком конкретному шляху. Почавши з кореня, ми скануємо ліве піддерево, якщо значення ключа менше поточного вузла. В іншому випадку сканується праве піддерево. Такий метод створення дерева дозволяє здійснювати пошук елемента по найкоротшому шляху від кореня. Наприклад, пошук числа 37 вимагає чотирьох порівнянь, починаючи з кореня.
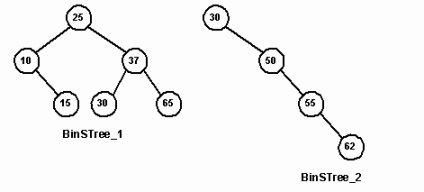
Мал. 11. Приклади дерев бінарного пошуку
На Рис. 11 вузли містять єдине цілочисельне значення, яке і є ключем. В цьому випадку вузол 25 має ключ 25, і ми порівнюємо два вузла шляхом порівняння цілих чисел. Порівняння проводиться за допомогою цілочисельних операторів відносини "<" и "==". Для студента университета ключом является ssn, и мы сравниваем две символьные строки. Это делается с помощью перегрузки операций. Например, следующий код реализует отношение "<" для двух объектов Student:
int operator <(const Student& s, const Student& t)
return s.ssn
У наших програмах ми наводимо низку прикладів ключ / дані. В ілюстраціях ми використовуємо простий формат, де ключ і дані - одне і те ж.
Робота з бінарним деревом пошуку
Бінарне дерево пошуку є нелінійної структурою для зберігання безлічі елементів. Як і будь-яка спискові структура, дерево повинно допускати вставку, видалення і пошук елементів. Для пошукового дерева потрібно така операція вставки, яка правильно розташовує новий елемент. Розглянемо, наприклад, вставку вузла 8 в дерево BinSTree_1. Почавши з кореневого вузла 25, визначаємо, що вузол 8 повинен бути в лівому поддереве вузла 25 (8<25). В узле 10 определяем, что место узла 8 должно быть в левом поддереве узла 10, которое в данный момент пусто. Узел 8 вставляется в дерево в качестве левого сына узла 10.
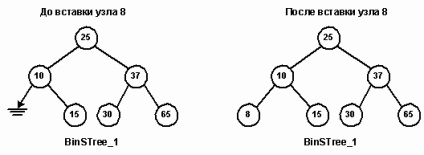
До кожного вставляється в дерево вузла існує конкретний шлях. Той же шлях може використовуватися для пошуку елемента. Пошуковий алгоритм бере ключ і шукає його в лівому або в правом поддереве кожного вузла, що становить шлях. Наприклад, пошук елемента 30 на дереві BinSTree_1 (Рис. 10) починається в кореневому вузлі 25 і переходить в праве піддерево (30> 25), а потім в ліве піддерево. (30 <37). Поиск прекращается на третьем сравнении, когда ключ совпадает с числом 30, хранящемся в узле.
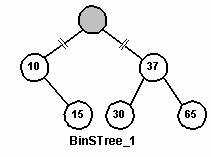
У пов'язаному списку операція видалення від'єднує вузол і з'єднує попередній йому вузол з наступним вузлом. На бінарному дереві пошуку подібна операція набагато складніше, тому що вузол може порушити упорядкування елементів дерева. Розглянемо задачу видалення кореня (має значення ключа 25) з BinSTree_1. В результаті з'являються два роз'єднаних поддерева, яким потрібен новий корінь.
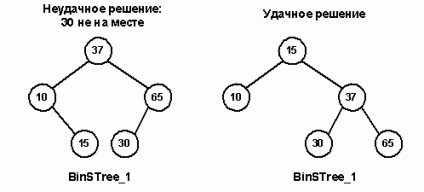
На перший погляд напрошується рішення вибрати сина вузла 25 - скажімо, 37 - і замінити його батька. Однак це просте рішення зазнає невдачі, так як деякі вузли виявляються не з того боку кореня. Оскільки дане дерево відносно невелике, ми можемо встановити, що 15 або 30 є допустимою заміною кореневого вузла.
// Специфікація класу BinSTree
template
cout <<"Студент отсутствует в базе данных." <
Використання бінарних дерев пошуку
Клас BinSTree - потужна структура даних, яка використовується для обробки динамічних списків. Перед розглядом прикладу практичного завдання побудови конкордансу розглянемо кілька більш простих прикладів. Під конкорданс тут розуміється алфавітний список всіх слів заданого тексту з покажчиками на місця їх появ. Розглянемо ряд простих програм, де застосовуються дерева пошуку.
Створення прикладів дерев пошуку.
У розділі «Структура бінарного дерева» функція MakeCharTree використовувалася для створення ряду бінарних дерев з символьними даними. Створимо схожу функцію MakeSearchTree, яка будує бінарні дерева пошуку з цілочисельними даними, застосовуючи метод Insert. Перше дерево SearchTree_0 створюється на базі масиву arr0. У цьому прикладі змінна Т має тип BinSTree.
for (i = 0; i <6; i++)
T.Insert (arr0 [i]); // Додати елемент до дерева
Ще два дерева, SearchTree_1 і SearchTree_2, створіть самі. Перше з них має бути восьміелементним деревом, а друге - деревом з десятьма випадковими числами з діапазону 10-99 (Рис. 12). Номер створюваного дерева повинен передаватися функції MakeSearchTree як параметр. Як інший параметра функція повинна отримувати покажчик на змінну типу BinSTree.
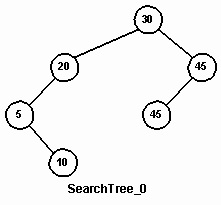
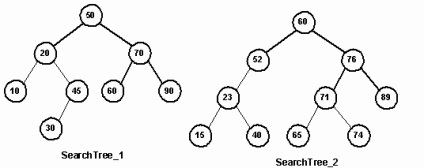
Мал. 12. Дерева, що створюються за допомогою функції MakeSearchTree
Симетричний метод проходження
При симетричному проходженні бінарного дерева спочатку відвідується ліве піддерево вузла, потім - сам вузол і нарешті праве піддерево. Коли цей метод проходження застосовується до бінарним дереву пошуку, вузли відвідуються в сортованому порядку. Цей факт стає очевидним, коли ви порівнюєте вузли в піддерево поточного вузла. Всі вузли лівого піддерева поточного вузла мають менші значення, ніж поточний вузол, і всі вузли правого піддерева поточного вузла більше або дорівнюють поточним вузлу. Симетричне проходження бінарного дерева гарантує, що для кожного вузла, який ми відвідуємо вперше, менші вузли знаходяться в лівому поддереве, а великі - в правом. В результаті вузли проходяться в порядку зростання.
Бінарне дерево пошуку може мати дубльовані вузли. В операції вставки ми продовжуємо сканувати праве піддерево, якщо наш новий елемент збігається з даними в поточному вузлі. В результаті в правому поддереве співпала вузла виникають дубльовані вузли.
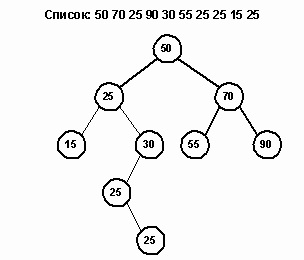
Наприклад, наступне дерево генерується зі списку 50 70 25 90 30 55 25 15 25.
Багато додатків не допускають дублювання вузлів, а використовують в даних поле лічильника примірників елемента. Це - принцип конкордансу, коли відслідковуються номера рядків, в яких зустрічається деякий слово. Замість того щоб кілька разів розміщувати слово на дереві, ми обробляємо повторні випадки вживання цього слова шляхом поміщення номерів рядків в список.
Реалізація класу BinSTree
Елементи даних класу BinSTree
Бінарне дерево пошуку визначається своїм покажчиком кореня, який використовується в операціях вставки (Insert), пошуку (Find) і видалення (Delete). Клас BinSTree містить елемент даних root, що є покажчиком кореня і має початкове значення NULL. Доступ до root здійснюється за допомогою методу GetRoot, який дозволить виклики зовнішніх функцій проходження. Другий покажчик, current, визначає на дереві місце для оновлень. Операція Find встановлює current на співпав вузол, і цей покажчик використовується функцією Update для поновлення даних. Методи Insert і Delete перевстановлюють current на новий вузол або на вузол, який замінив віддалений. Об'єкт BinSTree є списком, розмір якого весь час змінюється функціями Insert і Delete. Поточне число елементів в списку зберігається в закритому елементі даних size.
// Покажчики на корінь і на поточний вузол
// Число елементів дерева
Конструктор, деструкція і оператор присвоювання
template
BinSTree
// Не можна копіювати дерево в саме себе
if (this == rhs)
// Очистити поточний дерево.
// Скопіювати нове дерево в поточний об'єкт