Застосування одноступінчатої модуляції не дозволяє в багатьох випадках реалізувати переваги ЧТ і ФТ. Це пов'язано з тим, що в ідеальному випадку смуга пропускання радіоприймача повинна бути дорівнює спектру прийнятого сигналу. Практично ця вимога через нестабільність частоти несучої передавача і частоти гетеродина приймача реалізувати не вдається: смугу пропускання з урахуванням названих нестабільності частоти доводиться розширювати, що знижує стійкість. Тому, більш продуктивним виявляється двоступенева модуляція, при якій логічні 1 і 0 модулюють спочатку поднесущую порівняно низької частоти, а потім цією піднесе модулюють частоту несучої радіопередавача. Розглянемо більш докладно такий метод двоступеневої модуляції на прикладі ЧТ - ЧС, виконуваної згідно структурній схемі, наведеній на рис. 22.3.
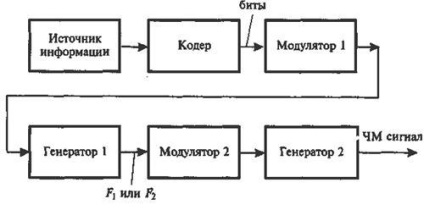
Мал. 22.3. Структурна схема двоступеневої модуляції ЧТ-ФМ
У першій щаблі модуляції сигнал, що надходить від джерела інформації, за допомогою кодує пристрої (кодера) перетвориться в послідовність двійкових символів - в біти інформації. Далі в модуляторі 1 логічної 1 присвоюється частота F1. а логічному 0 - F2 (при фазової модуляції їм присвоювалися б різні значення початкових фаз). Далі синусоїдальний сигнал з частотою F1 і F2 в другому ступені модулює з девіацією Dfдев частоту несучої радіопередавача. (В радіоприймачі такий сигнал двічі проходить процедуру демодуляції: спочатку виділяється частота піднесе, а потім - вихідне цифрове повідомлення - бітова послідовність - см. Рис. 22.1, а). При такій двоступеневої модуляції смуги пропускання фільтрів, що встановлюються в каналі частоти, що піднесе, вдається звузити до ширини спектра переданого повідомлення і тим самим підвищити стійкість перед перешкодами. Розглянемо, як потрібно вибирати частоти F1 і F2. По-перше, слід забезпечити «плавний» перехід, тобто без стрибка фази, від сигналу з частотою F1 до сигналу з частотою F2 так, як показано на рис. 22.1, б. Це викликано тим, що при стрибку фази відбувається «розмиття» миттєвого спектра сигналу, що знижує стійкість радиоприема і створює перешкоди іншим системам радіозв'язку. По-друге, значення цих частот, а точніше, співвідношення між ними, повинна бути такою, щоб енергетичний спектр модульованого сигналу був би сконцентрований в можливо вузькій смузі, або не був би «розмитий». По-третє, сигнали з частотами Fl і F2 повинні бути ортогональні. Ортогональними називають сигнали, що не перекриваються в часі і з незбіжними спектральними складовими в частотному спектрі.
Введемо поняття середнього значення частоти піднесе: F0 = 0,5 (F1 + F2) і різниці, чи дискрета частоти, DF = F1 -F2. Тоді для частот, що визначають відповідно логічні 1 і 0, запишемо:
де Fт = 1 / t - частота проходження елементарних посилок; К, N - числа, що показують, скільки періодів частоти піднесе укладається всередині елементарної посилки, т. Е. Усередині одного біта, причому К> N (рис. 22.1, б).
Для дискрета частоти маємо DF = F1 -F2 = Ft (K-N).
Фази сигналів усередині елементарних посилок на протязі одного біта змінюються згідно із законом:
- всередині біта логічної 1: j1 (t) = 2pF1 t = 2pF0 t + Dj (t);
- всередині біта логічного 0: j2 (t) = 2pF2 t = 2pF0 t + Dj (t), де додаткове зміна фази сигналу: Dj (t) = 2p0,5DFt = pFt (K-N) t.
До кінця елементарної посилки, тобто при t = t = 1 / Ft. додатковий набіг фази протягом одного біта складе:
- для логічної 1: Dj = + p (К-N);
- для логічного 0: Dj = -p (К-N).
При К = 1 + N значення Dj = + p для логічної 1 і Dj = -p для логічного 0. Такий випадок при К = 4 і N = 3 представлений на рис. 22.4, а, де логічна одиниця - F1 = 4Ft; логічний нуль - F2 = 3Ft. Можна, наприклад, вибрати такі значення параметрів:
t = 1,28 мс або Ft = 781,25 Гц; F1 = 3125 Гц; F2 = 2343,75 Гц.
Розкладемо в ряд Фур'є періодичне коливання прямокутної форми (меандр):
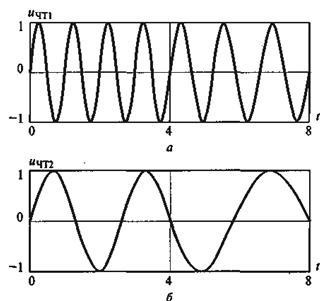
Мал. 22.4. Форми бітових посилок при ЧС для 1 і 0
З розгляду отриманого спектра слід, що основна енергія сигналу зосереджена в смузі DF = 5Ft. а вибрані сигнали ортогональні.
Такий спектр можна ще більше звузити при К = 1,5 і N = 1, тобто при логічної 1, представленої трьома напівперіодами сигналу з частотою F1 всередині одного біта і двома напівперіодами частоти F2 всередині біта для логічного 0 (рис. 22.4, б). При цьому, згідно з отриманим вище висловом набіг фази протягом одного біта складе для логічної 1: Dj = + p / 2; для логічного 0: Dj = -p / 2. Такий випадок частотної маніпуляції називається маніпуляцією з мінімальним зрушенням (мається на увазі мінімальний зсув фази) - спосіб MSK (Minimum Shit Keying). формувати сигнали при частотної маніпуляції, наведені на рис. 22.4, можна за допомогою процесора за спеціальною програмою.
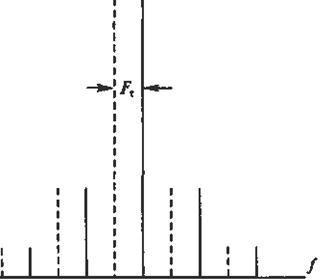
Мал. 22.5. Спектр сигналу при ЧМ бітових посилок
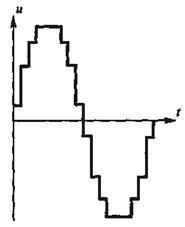
Мал. 22.6. Квазісінусоідальние сигнал, складений зі сходинок
При ЧС, як і при квадратурної ФМ, можна попарно передавати біти, використовуючи при цьому чотири значення частоти, і тим самим вдвічі збільшити обсяг інформації (табл. 22.2).
Висновки до розділу
1. Застосування одноступінчатої модуляції не дозволяє в багатьох випадках реалізувати переваги ЧТ і ФТ. Це пов'язано з тим, що в ідеальному випадку смуга пропускання радіоприймача повинна бути дорівнює спектру прийнятого сигналу. Практично ця вимога через нестабільність частоти несучої передавача і частоти гетеродина приймача реалізувати не вдається: смугу пропускання з урахуванням названих нестабільності частоти доводиться розширювати, що знижує стійкість.
Питання для самоконтролю:
1. У чому полягають відмінності частотної та фазової модуляції при передачі дискретних повідомлень?
2. Як здійснюється двоступенева частотна модуляція при передачі дискретних повідомлень?
3. Як виглядає сигнал з двоступеневої частотної модуляцією при передачі дискретних повідомлень?
4. Як змінюється фаза сигналу при відносній фазової модуляції?
5. Що називається квадратурної фазової модуляцією?
Вивчивши матеріал глави, дайте відповідь на питання. При виникненні труднощів зверніться до матеріалів для закріплення знань в кінці посібника. Для поглибленого вивчення скористайтеся літературою: основний: 16 - 17; додаткової: 4 - 6 і повторіть основні визначення, наведені в кінці посібника.