Переклад: Ткаченко С.В.
Джерело: Open System Resuorces Online
анотація:
Однією з основних проблем електрокардіографії, з боку області біомедичної обробки даних, є відділення корисного сигналу від перешкод викликаних ЛЕП перешкодами, зовнішніми електромагнітними полями, випадковими рухами тіла і дихання. В даний момент, для очищення сигналу від небажаних частотних діапазонів застосовуються різні типи цифрових фільтрів. Однак, для зменшення перешкод біомедичних сигналів важко застосовувати фільтри з фіксованими коефіцієнтами, тому що поведінка людини не можна в точності передбачити. Адаптивна фільтрація є технікою, необхідною для подолання цієї проблеми. У цій статті представлені кілька типів адаптивних фільтрів, призначених для зниження рівня перешкод в ЕКГ сигналах, наприклад, PLI і фільтрації з базовою лінією перешкод. Представлені результати моделювання роботи фільтрів в MATLAB. У даній статті використовується рекурсивний метод найменших квадратів (RLS). RLS алгоритм пропонується використовувати для видалення артефактів з низьких частотних складових сигналу. Алгоритм найменших квадратів спрямований на мінімізацію суми квадратів різниці між корисним сигналом і моделлю вихідного фільтра. Коли нові зразки вхідних сигналів надходять на кожній ітерації, вирішення проблеми знаходження для них найменших квадратів може бути обчислено в рекурсивної формі, в результаті рекурсивного виклику алгоритму найменших квадратів (RLS). RLS алгоритми, як відомо, володіють швидкою збіжністю, навіть для випадків коли значення кореляційної матриці вхідного сигналу великі. Ці алгоритми мають відмінну продуктивність при роботі в нестаціонарних умовах. Всі ці переваги неминуче супроводжуються підвищенням обчислювальної складності та деякими проблемами зі стабільністю, але ці проблеми не критичні для алгоритмів заснованих на LMS.
Ключові слова: ЕКГ сигнал, умови Діріхле, адаптивний фільтр.
1. ВВЕДЕННЯ
Зняття ЕКГ сигналів з високою роздільною здатністю, забруднених фоновими перешкодами, є важливим питанням для проведення досліджень. Метою цих досліджень є поліпшення сигналу ЕКГ. Для полегшення точної інтерпретації ЕКГ необхідно відокремити допустимі компоненти сигналу від небажаних артефактів. Багато підходів для цього були описані в літературі для поліпшення ЕКГ з використанням адаптивних фільтрів [1] - [3]. Такі фільтри дозволяють виявляти різні потенціали часу і відстежувати динамічні зміни сигналів. У роботах [4] - [6] запропоновано адаптивний фільтр, заснований на LMS, для періодичного отримання імпульсного відгуку нормальних комплексів QRS. Потім даний фільтр застосовується для виявлення аритмій в амбулаторних записах ЕКГ. Входи в алгоритм LMS є детермінованими функціями і визначаються періодичними розширеннями, які, в свою чергу, є усіченим набором ортонормованих базисних функцій.
У цих роботах, алгоритм LMS працює на основі миттєвого базису, такого, як вага вектора, який оновлюється для кожного нового зразка, на основі миттєвої оцінки градієнта. Є певні клінічні додатки обробки сигналів ЕКГ, які вимагають адаптивних фільтрів з великим числом запусків. У таких випадках звичайний алгоритм LMS неприйнятний через високі вимоги до обчислювальних ресурсів. LMS алгоритм і NLMS (нормований LMS) алгоритми вимагають кілька розрахунків, і, отже, широко застосовуються для акустичних луна заглушувачів. RLS (рекурсивний алгоритм найменших квадратів) алгоритм, збіжність якого не залежить від вхідного сигналу, є найшвидшим з усіх традиційних адаптивних алгоритмів. Основним недоліком алгоритму RLS є великі обчислювальні витрати. Проте, останнім часом, розроблені швидкі RLS алгоритми. У цій статті ми хочемо отримати більш швидкий алгоритм, що включає знання номера імпульсу в алгоритм RLS. На відміну від NLMS і інших проекційних алгоритмів, RLS алгоритм не має скалярного розміру кроку. Таким чином, зміна характеристик сигналу ЕКГ не може бути відображено безпосередньо в алгоритмі RLS. Тут ми вивчаємо RLS алгоритм з точки зору адаптивних фільтрів, тому що (а) RLS алгоритм можна розглядати як спеціальну версію адаптивного фільтра і (б) кожен параметр адаптивного фільтра має фізичне значення. Комп'ютерне моделювання показує, що цей алгоритм сходиться в два рази швидше звичайного базового алгоритму. Це може відігравати важливу роль в біотелеметрії, де зняття без перешкод ЕКГ сигналу для ефективного діагностування та висока швидкість передачі даних необхідні, щоб уникнути дублювання імпульсів і вирішення невизначеностей. Наскільки нам відомо, перетворення доменів не було розглянуто раніше в контексті фільтрації перешкод сигналів ЕКГ. У цій статті ми представляємо RLS алгоритм для видалення перешкод на ЕКГ. Цей алгоритм має меншу обчислювальну складність і хороші можливості фільтрації. Для вивчення ефективності запропонованого алгоритму ефективного видалення перешкод з сигналу ЕКГ, було проведено моделювання за допомогою MIT-BIH бази даних для різних перешкод.
2. ПРИНЦИП: РЯД ФУР'Е
Будь-які періодичні функції, що задовольняють умовам Діріхле, можуть бути виражені у вигляді ряду масштабних величин синуса або косинуса з точки зору частоти, з якою відбуваються коливання, кратні основній частоті.
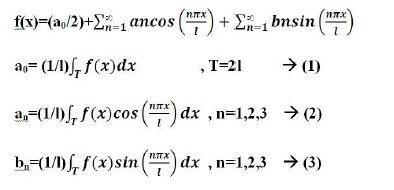
ЕКГ сигнал є періодичним, з частотою рівною серцебиття. Він також задовольняє умовам Дирихле:
Як можна спостерігати на малюнку 1, один період ЕКГ сигналу являє собою суміш трикутної і синусоїдальної форми хвилі. Кожна істотна особливість ЕКГ сигналу може бути представлена зрушеною і промасштабірованной версією однієї з таких осциллограмм, як показано нижче.
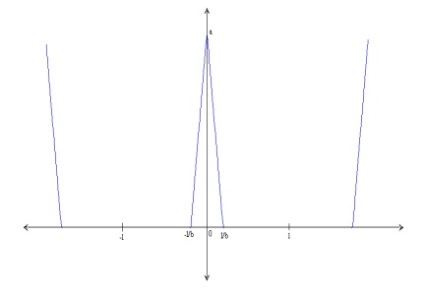
Мал. 1. Осцілограмма QRS
З виразу (1), маємо:

Генерація періодичних p-хвильових частин ЕКГ сигналу:
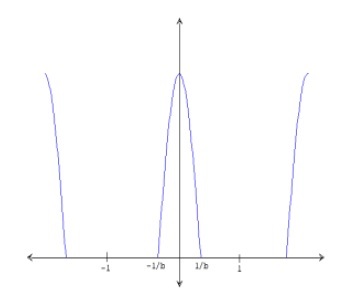
Мал. 2. Осцілограмма p-хвильової частини сигналу

4. помехоподавленія
Комбінований з перешкодами сигнал подається на "основний вхід" в компенсатор. Другий датчик отримує перешкоду n1, яка не корелює з сигналом, але корелювала деяким невідомим шляхом з перешкодою n0. Цей датчик забезпечує "вхідний відношення" в компенсаторі. Перешкода n1 фільтрується, щоб виробляти висновок "у", який є близькою копією n0. Цей висновок віднімається з основного входу "s + n0" для створення системного виходу s + n0-y. Якщо відомі характеристики каналів, по яких передані перешкоди в первинні і вторинні датчики, можна створити фіксований фільтр порівняння змін n1 в у = n0. Вихід фільтра потім може бути вирахувано з основної входу, і вихід системи буде містити еденічние сигнал. Однак, оскільки, характеристики шляхів передачі вважаються невідомими або відомі лише приблизно, використання фіксованого фільтра не представляється можливим. Більш того, навіть якщо використання фіксованого фільтра було можливо, його характеристики повинні бути скоректовані з важко досяжною точністю, і найменша помилка може призвести до посилення перешкоди. В системі, показаної на рис. 3, вторинний вхід обробляється за допомогою адаптивного фільтра, який автоматично налаштовує свій імпульсний відгук за методом найменших квадратів. Такі алгоритми як RLS реагують на величину сигналу помилки на виході фільтра. У системах помехоподавленія практична мета полягає в створенні системи вироблення системного виходу s + n0-y, який найкраще відповідає сигналу s, з урахуванням методу найменших квадратів. Ця мета досягається шляхом подачі системного виходу назад на адаптивний фільтр і налаштування фільтра через адаптивний алгоритм для мінімізації загальної потужності системи. Іншими словами, в системах адаптивного помехоподавленія, системний вихід використовується як помилка сигналу для адаптивного процесу.
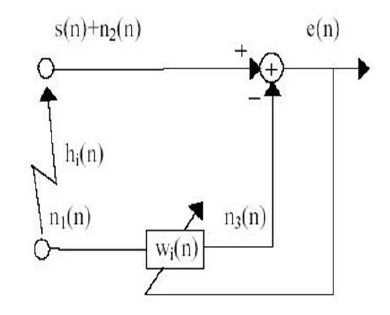
Мал. 3. Адаптивний помехоподавітель
5. RLS АЛГОРИТМ
Метою роботи алгоритму є вибір коефіцієнтів адаптивного фільтра таким чином, щоб вихідний сигнал у (k), протягом періоду спостереження, відповідав корисного сигналу, наскільки це можливо в сенсі найменших квадратів. Процес мінімізації вимагає доступної інформації про вхідному сигналі в попередній момент часу. Крім того, цільова функція, до якої ми прагнемо мінімізувати, є детермінованою. Загальний FIR адаптивний фільтр реалізований в прямій формі на рис. 3. Інформація про вхідному сигналі в даний момент знаходиться в векторі k.
зворотна детермінована кореляційна матриця може бути розрахована в наступному вигляді:
Повний RLS алгоритм описаний в алгоритмі 5.1.

6. РЕЗУЛЬТАТИ МОДЕЛЮВАННЯ
Щоб показати, що RLS алгоритм дійсно ефективний в клінічних ситуаціях, цей метод був перевірений за допомогою декількох записів ЕКГ з широким спектром хвильових морфології з MIT-BIH бази даних аритмії. У нашій роботі ми використовували ЕКГ сигнали забруднені перешкодами різної частоти, які були оцифровані в 200 вибірок в секунду на кожен канал з 20 мВ в діапазоні. Проте, реальні перешкоди можуть бути отримані з бази даних нормального синусового ритму (NSTDB).
A. Адаптивна фільтрація перешкод від харчування
Перешкоди на лінії електропередачі можуть призвести до серйозного пошкодження біомедичних записів. Ми пропонуємо покращений адаптивний компенсатор для скорочення основної складової перешкоди лінії електропередачі і гармоніки в електрокардіограмі (ЕКГ). Метод відстежує амплітуду, фазу і частоту всіх перешкод для лінії електропередачі для частот приблизно до 4 Гц. Очищений сигнал після застосування всіх методів порівнюється з початковим сигналом ЕКГ. Наш покращений адаптивний компенсатор показує відношення до потужності зони прямої перешкоди для основних компонентів до 30 дБ вище, ніж при інших методах. Крім того, наш метод ефективний також для придушення гармонік перешкод лінії електропередачі. Щоб продемонструвати мощностную перешкоду (PLI) ми вибрали моделювання синусоїдальної хвилі частотою 50 Гц.
B. Базове блукаюче скорочення
Забруднене ЕКГ сигнал поданий на головний вхід адаптивного фільтра на рис. 3.
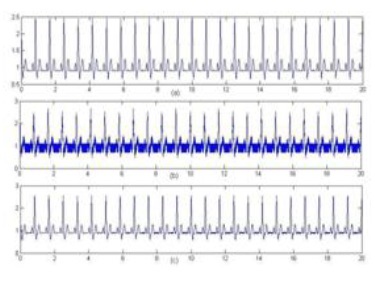
Мал. 4. a) Чистий ЕКГ сигнал, b) ЕКГ з PLI перешкодою, c) Відфільтрований по RLS алгоритму.
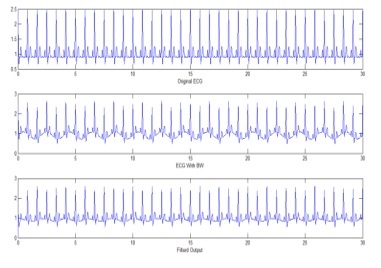
Мал. 5. a) Чистий ЕКГ сигнал, b) ЕКГ з BW перешкодою, c) Відфільтрований по RLS алгоритму.
C. Адаптивна фільтрація м'язових перешкод.
Щоб показати ефективність фільтрації в присутності нестаціонарних перешкод, м'язові перешкоди (MA) були взяті з MIT-BIH бази даних. Часто ЕКГ бувають забруднені електрофізіологічними потенціалами, пов'язаними зі скороченням м'язів людини. Такі м'язові артефакти ускладнюють інтерпретацію ЕКГ або навіть роблять її неможливою. Для видалення таких перешкод використовуються низькочастотні фільтри. Однак, частотний спектр м'язових перешкод може перетинатися з частотою сигналів мозку. Таким чином фільтри пригнічують не тільки м'язові перешкоди, але і цінну інформацію.
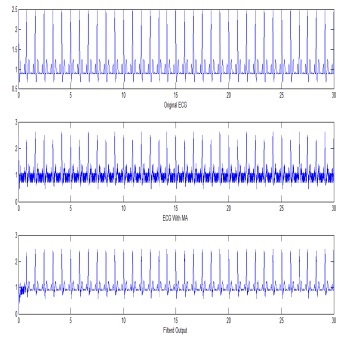
Мал. 6. a) Чистий ЕКГ сигнал, b) ЕКГ з MA перешкодою, c) Відфільтрований по RLS алгоритму
D. Адаптивне зняття з електрода
Для демонстрації цього ми використовуємо чистий сигнал ЕКГ знятий з електродів, з додаванням EM перешкоди. EM перешкода створюється з частотою вище 15 Гц. Сигнал ЕКГ, забруднене EM перешкодою, подається на вхід адаптивного фільтра. EM перешкода використовується як опорний сигнал. На виході фільтра отримуємо необхідне високе дозвіл сигналу ЕКГ. Результати наведені на рис. 7.
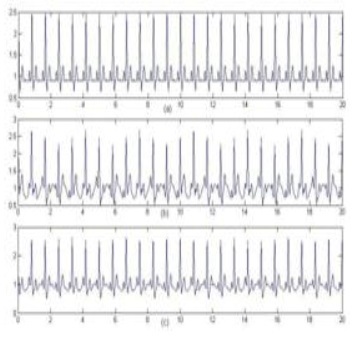
Мал. 7. a) Чистий ЕКГ сигнал, b) ЕКГ з EM перешкодою, c) Відфільтрований по RLS алгоритму.
У даній роботі представлений процес видалення перешкод з ЕКГ сигналу заснований на використанні RLS адаптивного фільтра. Для цього, вхідний і корисний сигнали обрані таким чином, що вихідний фільтр виводить кращу мінімальну квадратну оцінку вихідного сигналу ЕКГ. Запропонований метод використовує зміни у формулі поновлення ваги і, отже, призводить до зростання швидкості по відношенню до відповідних LMS заснованим реалізацій. У наших дослідженнях, однак, підтверджено, що SNR запропонованого алгоритму дає кращий результат. Крім того, швидкість збіжності швидше, а також складність обчислень менше, ніж для LMS реалізацій. Результати наведені в таблиці 1.
SNR до фільтрації (в dbs)