Тема: Елементи теорії тригонометричних функцій
Урок: Числова окружність
1. Тема уроку, введення
Наша найближча мета - визначити тригонометричні функції: синус. косинус. тангенс. котангенс-
2. Числова окружність
Числовий аргумент можна відкладати на координатної прямої або на колі.
Така окружність називається числовий або одиничної, т. К. Для зручності беруть окружність з
Наприклад, дана точка Відзначимо її на координатної прямий
і на числової окружності.
При роботі з числовою окружністю домовилися, що рух проти годинникової стрілки - позитивний напрямок, за годинниковою стрілкою - негативне.
Типові завдання - потрібно визначити координати заданої точки або, навпаки, знайти точку по її координатами.
Координатна пряма встановлює взаємно-однозначна відповідність між точками і числами. Наприклад, числу відповідає точка А з координатою
Кожна точка В з координатою характеризується тільки одним числом - відстанню від 0 до узятим зі знаком плюс або мінус.
На числової окружності взаємно-однозначна відповідність працює тільки в одну сторону.
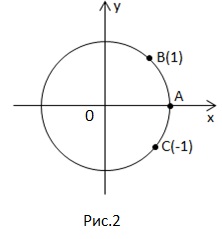
Наприклад, є точка В на координатної окружності (рис.2), довжина дуги дорівнює 1, т. Е. Ця точка відповідає 1.
Дана окружність, довжина кола Якщо то - довжина одиничному колі.
Якщо ми додамо, отримаємо ту ж точку В, ще - теж потрапимо в т. В, віднімемо - теж т. В.
Розглянемо точку B: довжина дуги = 1, тоді числа характеризують т. В на числової окружності.
Таким чином, числа 1 відповідає єдина точка числової окружності - точка В, а точці В відповідає безліч точок виду.
Для числової окружності вірно наступне:
Якщо т. М числової окружності відповідає числу то вона відповідає і числу виду
Можна робити скільки завгодно повних обертів навколо числовий окружності в позитивному або негативному напрямі - точка одна і та ж. Тому тригонометричні рівняння мають безліч рішень.
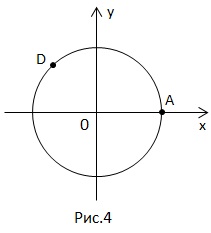
Наприклад, дана точка D. Які числа, яким вона відповідає?
безліч всіх чисел, відповідних точці D.
3. Основні точки окружності
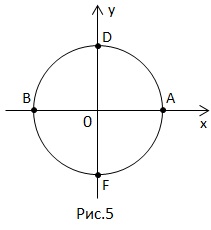
Розглянемо основні точки на числовій окружності.
довжина всьому колу.
.
Т. е. Запис безлічі координат може бути різною.
4. Приклади
Розглянемо типові завдання на числову окружність.
1. Дано:. Знайти: точку на числовій окружності.
Виділяємо цілу частину:
.
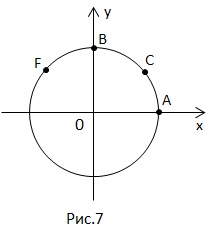
Необхідно знайти т. На числової окружності. , Тоді.
У цей безліч входить і крапка.
2. Дано:. Знайти: точку на числовій окружності.
Необхідно знайти т.
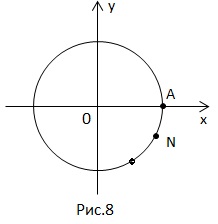
т.также належить цій безлічі.
Вирішуючи стандартні завдання на відповідність між числами і точками на числовій окружності, ми з'ясували, що можна для кожного числа знайти єдину точку, і можна для кожної точки знайти безліч чисел, які характеризуються цією точкою.
Розділимо дугу на три рівні частини і відзначимо точки M і N.
Знайдемо всі координати цих точок.
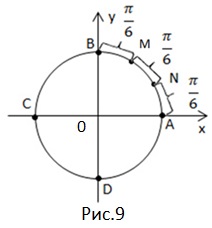
5. Висновок
Отже, наша мета - визначення тригонометричних функцій. Для цього нам необхідно навчитися ставити аргумент функції. Ми розглянули точки одиничного кола і вирішили дві типові завдання - знайти точку на числовій окружності і записати всі координати точки одиничному колі.
Список рекомендованої літератури
Рекомендовані посилання на ресурси інтернет
1. Відкрита математика.
Рекомендоване домашнє завдання
№№ 531; 536; 537; 541; 552.
Завантаження.
Завантаження.
Популярні твори
- Пейзажі в ліриці А. С. Пушкіна
- Аналіз вірша А. Блоку «На полі Куликовому»
- Батько і син в оповіданні Д. Олдріджа "Останній Дюйм"
- Життя і творчість Гете В. І
- Рішення арбітражного суду. завдання
- Проектування підприємства громадського харчування Проектування закусочної. Частина 2
- А. С. Пушкін і С. А.Есенін про російську природу
-
Статистика проекту
Схожі статті