відомий американський астроном С.Ньюком (1835-1909) математично довів неможливість створення літальних апаратів, важчих за повітря.
Якщо запитати перехожого, чому літає літак, він дотепно відповість: по небу (по чому). І буде неправий - як ми побачимо, літак літає ... по землі!
Для початку згадаємо відому задачу. На чашках ваг стоять дві непрозорі коробки. В одній з них сидить муха, в іншій - така ж муха літає. Що покажуть ваги? Відповідь: нуль. Тому що літаюча муха, для того щоб триматися в повітрі, створює потік імпульсу, в точності рівний її вазі. Цей потік імпульсу (вага мухи), спрямований вниз, передається на дно коробки, врівноважуючи муху, яка сидить в іншій коробці.
Може бути, не всім зрозуміло, що таке потік імпульсу? Тоді розглянемо ще один приклад.
На муху дуже схожий вертоліт, нерухомо висить в повітрі. Що дозволяє йому не падати? Гвинт «засмоктує» повітря, який далеко ( «на нескінченності») покоїться (v ∞ = 0) = 0 \ right)>. і відкидає його вниз зі швидкістю v. Звичайно, це повітря рано чи пізно повертається на своє місце, так що вертоліт створює вихрове кільце, перемішуючи всю атмосферу, як показано (якісно) на рис.1.
Якщо позначити щільність повітря через ρ кг / м³ (а при дозвукових швидкостях щільність потоку можна вважати постійної), то маса повітря, що перетікає в одиницю часу через перетин S зі швидкістю v. дорівнює μ = ρ v S [кг / м³ ⋅ м / с ⋅ м² = кг / с].
Нагадаємо висновок цієї формули. Витрата Q [м³ / c] - це обсяг рідини або газу, що протікає через поперечний переріз потоку або труби в одиницю часу: Q = Δ V Δ t >>.
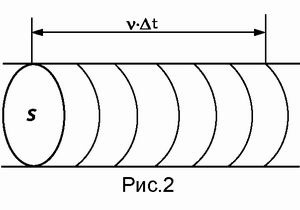
Нехай S - площа поперечного перерізу потоку, v - його швидкість. Тоді за проміжок часу Δ t через поперечний переріз s пройде обсяг Δ V = s ⋅ v ⋅ Δ t (Рис.2). Тоді Q = Δ V Δ t = s ⋅ v> = s \ cdot v> і μ = ρ ⋅ Q = ρ ⋅ s ⋅ v. Цю величину природно назвати потоком маси. А якщо розділити її на площу перетину потоку, отримаємо щільність потоку маси μ S = ρ v> = \ rho v> [кг / (м² ⋅ с)]
Ви запитаєте при чому тут земля і матимете рацію - НІ ЗА ЩО.
Тепер похилій площині гвинта вертольота «вперед» (рис.3)
Розкладемо силу його тяги на вертикальну компоненту Y і горизонтальну X. Вертоліт полетить в напрямку сили X, компонента Y, звичайно, повинна залишитися рівній вазі, а X урівноважиться силою опору повітря. У літака ролі в створенні цих двох сил розділені: крило створює вертикальну (підйомну) силу, а мотор - силу тяги. (Детальніше б: "крило створює вертикальну (підйомну) силу," - а як?) Причому крило має чудову властивість: воно здатне створювати підйомну силу набагато більшу, ніж сила опору повітря його руху. Фізик сказав би - на порядок більшу. Це, звичайно, не означає «рівно в 10 разів більшу», - це може бути і 8, і 20. Ставлення цих двох сил називається якістю крила Y X = K> = K>. Отже, на відміну від вертольота, крилатий літальний апарат потребує силі тяги, на порядок менший ваги апарату (а адже вертоліт навіть для нерухомого висіння повинен володіти підйомної силою, неменшою ваги, - а тим більше для горизонтального переміщення).
Приблизно півсотні років літаки використовували тягу гвинта-пропелера. Сучасні літаки використовують реактивні двигуни. Але фізичний принцип однаковий: будь-який двигун повинен створювати потік імпульсу.
Оцінимо, з якою швидкістю двигун літака повинен відкидати масу газу назад. Якщо вага літака дорівнює G, якості крила К, а ми збираємося використовувати N двигунів, то кожен з них повинен створити силу тяги G / KN. Далі, якщо на виході з двигуна площею перетину S щільність газів дорівнює ρ s> швидкість витікання v, то потік маси в системі координат, пов'язаної з літаком, μ = ρ sv S.> \ Rho _ >>>> [кг / с] . Будемо вважати приблизно, що він дорівнює потоку маси на вході в двигун. Це означає, що ми нехтуємо додаткової масою згорілого палива - роль останнього, таким чином, зводиться до нагрівання повітря, а не до збільшення витрати маси - і чим менше витрата палива, тим економічніше авіадвигун. Тоді, в результаті нагрівання повітря, що проходить через двигун, його швидкість (а це ж, як ми пам'ятаємо, питома імпульс) збільшується на v-u, де u - швидкість польоту (рис.4).
Таким чином, зміна імпульсу (а це і є тяга одного двигуна) одно F 1 = μ (vu) = ρ su S (vu) = G / K N. = \ mu (vu) = \ rho _uS ( vu) = G / KN.> Припустимо, що тиск газів на виході з двигуна в точності дорівнює тиску навколишньому повітрі (індекс ∞), а їх температура дорівнює Ts. Тоді щільність знайдемо із закону Менделєєва-Клапейрона: ρ s = p ∞ / R T s. = P_ / RT _,> де R = R 0 / M / M> - газова постійна, R 0 = 8. 31 = 8,31> Дж / К ⋅ моль, M = 29 ⋅ 10 - 3> кг / моль - молярна маса повітря. До речі, звертаємо увагу, що щільність вихлопних газів ρ s> взагалі не повинна дорівнювати щільності атмосфери, що і підкреслює індекс s.
Зробимо чисельні оцінки. Розглянемо сучасний авіалайнер вагою G = 400 T = 4 ⋅ 10 6 HH> має N = 4 двигуна радіусом r вихідного перетину один метр, що летить з дозвуковій швидкістю u = 250 м / с на висоті більше 10 км, тиск атмосфери в п'ять разів менше тиску на рівні моря, p ∞ = 10 5/5 = 2 ⋅ 10 4 = 10 ^ / 5 = 2 \ cdot 10 ^> Па. Чому дорівнює Ts. Підставами ці числа в рівняння
F 1 = p ∞ / RT sv π r 2 (vu) = G / KN = 4 ⋅ 10 6 / (10 ⋅ 4) = 10 5 H = p_ / RT_v \ pi r ^ (vu) = G / KN = 4 \ cdot 10 ^ / (10 \ cdot 4) = 10 ^ H>
Вирішуючи це квадратне рівняння (щодо v), знайдемо v ≈ 500 м / с.
Звичайно, такий двигун (у якого радіус вихідного перетину порядку метра) може належати тільки дуже великим трансатлантичному лайнеру. Але чому вигідно будувати великі літаки? На це відповідає теорія подібності, яку знали ще за часів Джонатана Свіфта. Ось що пише з цього приводу очевидець Гуллівер: «Математики його величності, визначивши висоту мого зросту за допомогою квадранта і знайшовши, що висота ця знаходиться в такому ставленні до висоти ліліпута, як дванадцять до одиниці, уклали на підставі подібності наших тіл, що обсяг мого тіла дорівнює, принаймні, обсягом 1728 тел ліліпутів, а отже, воно вимагає в стільки ж разів більше їжі ». Іншими словами, якщо ліліпутів покладається один бутерброд, то Гулліверу - 12³ бутербродів. Ясно, що тут закладено припущення про однаковість масової щільності тел ліліпута і Гуллівера.
Інша справа - літальний апарат. Як видно з виразу (1), підйомна сила пропорційна НЕ обсягом, а площі поверхні. Значить якщо збільшити характерний розмір літака в N раз, його обсяг збільшиться в N³ раз, а площа крила і, отже, вага - в N² раз. Це тому що літак - оболонка, а не суцільне тіло. (Зрозуміло, що в цих міркуваннях ρ v 2> - так званий швидкісний натиск - вважаємо фіксованим).
Так, але! - вигукне уважний читач - адже формула (1) отримана для вертольота, а ми говоримо вже про літаки? Тут треба заспокоїти уважного читача такими словами: Ви маєте рацію, але якщо визнати, що аеродинамічна сила, що діє на літальний апарат, залежить від щільності середовища ρ [кг / м³], швидкості руху v [м / c], і його розміру L [м ], то єдиною комбінацією цих величин, що має розмірність сили, буде ρ v 2 L 2 L ^> [кг / м³ ⋅ м² / с? ⋅ м² = кг ⋅ м / с?]. Звичайно, для визначення чисельного значення цієї сили треба було б врахувати ще невідомий безрозмірний множник, - але ж нас цікавили тільки відносини сил, а не їх величина.
Отже, на якій висоті ні летів би літак, він просто зобов'язаний створювати рівний по вазі потік імпульсу, спрямований вниз і, врешті-решт, спиратися на землю.
Але, звичайно, справа не тільки в мухах, вертольотах і літаках. Розглянуті нами поняття потоків і щільності потоків досить часто зустрічаються в багатьох розділах фізики. Це дуже корисні поняття. Ви, напевно, вже здогадалися, що можна ввести не тільки поняття потоку маси і імпульсу, але і інших фізичних величин: потоку моменту імпульсу (якщо щось обертається), потоку енергії, потоку електричного заряду (також званого силою струму), потоку індукції магнітного поля ... та хіба мало чого ще. Але на перший раз досить сказаного.
Так що якщо ви повідомите близьким, друзям і знайомим, що швидкість - це питома імпульс, а сила є потік імпульсу, ви будете абсолютно праві. А якщо ще додасте, що тиск є щільність потоку імпульсу, ви зарекомендуєте у своїй школі дуже розумним і напевно зробите в МФТІ.
1. Оцінити мінімальний витрата (потік маси) палива N μ T.,> необхідний для забезпечення сили тяги літака, розглянутого в тексті. При згорянні одного кілограма палива виділяється енергія r, Дж / кг (теплотворна здатність). Вважати, що ця енергія йде на подолання сили опору (потужність N F 1>) і зміна кінетичної енергії газів (до і після проходження двигунів). Втратами теплової енергії знехтувати. Для гасу прийняти r = 40 МДж / кг.
2. Порівняти знайдений витрата палива з витратою повітря.
3. Оцінити площу крил розглянутого літака.