хвиля, радіально розходяться від (сходиться к) деякої осі в просторі або точці на площині. В останньому випадку ці хвилі зв. також круговими. Прикладами Ц. в. можуть служити хвиля на поверхні води від кинутого каменя або вагається поплавка, електромагніт. або акустич. хвилі, порушувані джерелами, розташованими в просторі, обмеженому, напр. двома плоскопараллельнимі відбивачами (в т. ч. усередині океанич. волноводов і т. д.).
Структура Ц. в. істотно складніше структури плоских (одновимірних) і сферич. (Тривимірних) хвиль. Найпростіша монохроматічен. симетрична Ц. в. з джерелом в центрі (рис. 1) задовольняє двовимірному хвильовому рівнянню і описується за допомогою функції Ханкеля нульового порядку H0 (kr):
де з - кругова частота, k - хвильове число. На великих відстанях від осі (kr -> 1) хвильове поле (1) набуває вигляду:
u (r, t) = (A /? r) exp (wt-kr), (2)
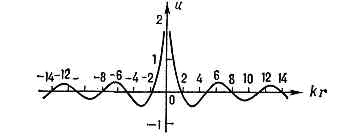
Мал. 1 Радиально розходиться цилиндрич. хвиля, що збуджується джерелом в центрі.
і тільки в цьому асімптотіч. поданні в Ц. в. можна однозначно виділити амплітуду А /? r і фазу wt-kr = w (t-r / vф), де фазова швидкість vф збігається з фазовою швидкістю плоскої хвилі: vф = w / k = 2p / l (l- довжина хвилі). У міру віддалення від осі квадрат модуля хвильового збурення (2) убуває як 1 / r, а поверхню циліндра, що охоплює джерело, росте пропорційно r, так що, відповідно до закону збереження енергії, сумарне значення потоку енергії, що буря від джерела на осі, залишається постійним. При відсутності дисперсії хвиль з гармонич. хвиль (2) далеко від осі можна скласти хвилю будь-якої форми (зокрема, відокремлене хвилю, або хвильової пакет), що переміщається з постійною швидкістю vф = v
де ф-ція f (t-r / v) задовольняє одномерному хвильовому ур-нію. Однак в проміжній області, де kr = 1,
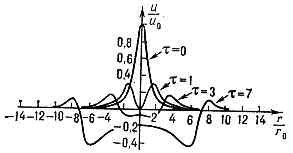
Мал. 2. Радиально розходиться цилиндрич. хвиля, задана в початковий момент часу в формі одиночного імпульсу u = u0 / (1 + r / r0) 3/2. Зі збільшенням t = ct / r0 (з ростом часу t) імпульс розпливається, залишаючи за собою «шлейф».
навіть в середовищі без дисперсії відбувається сильна деформація хвильового збурення (рис. 2). Це пов'язано з тим, що Ц. в. в принципі нестаціонарна: віддаляючись від осі (центру), вона залишає за собою «шлейф», к-рий можна інтерпретувати як результат приходу хвильових збурень від все більш і більш віддалених від точки спостереження джерел на осі.
- хвиля, радіально розходяться від або сходиться до деякої осі в просторі або точці на площині. В останньому випадку ці хвилі зв. також круговими. Прикладами Ц. в. можуть служити хвиля на поверхні води від кинутого каменя або вагається поплавка, електромагнітного магн. або акустич. хвилі, порушувані джерелами, розташованими в просторі, обмеженому, напр. двома плоскопараллельнимі відбивачами (в т. ч. усередині океанич. волноводов і т. д.).
Структура Ц. в. істотно складніше структури плоских (одновимірних) і сферич. (Тривимірних) хвиль. Найпростіша монохроматічен. симетрична Ц. в. з джерелом в центрі (рис. 1) задовольняє двовимірному хвильовому рівнянню і описується за допомогою ф-ції Ханкеля нульового порядку H0 (kr):
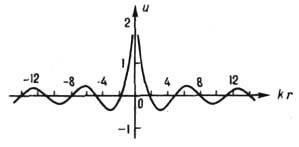
Мал. 1. Радіально розходиться циліндрична хвиля, що збуджується джерелом в центрі.
де w - кругова частота, k - хвильове число. На великих відстанях від осі (kr >> 1) хвильове поле (1) набуває вигляду
і тільки в цьому асімптотіч. поданні в Ц. в. можна однозначно виділити амплітуду А /. і фазу wt-kr = w (t -r / u ф), де фазова швидкість u ф збігається з фазовою швидкістю плоскої хвилі: u ф = w / k = 2p / l (l - довжина хвилі). У міру віддалення від осі квадрат модуля хвильового збурення (2) убуває як 1 / r, а поверхню циліндра, що охоплює джерело, росте пропорційно r, так що, відповідно до закону збереження енергії, сумарне значення потоку енергії, що буря від джерела на осі, залишається постійним.
За відсутності дисперсії хвиль з гармонич. хвиль (2) далеко від осі можна скласти хвилю будь-якої форми (зокрема, відокремлене хвилю або хвильової пакет), що переміщається з пост. швидкістю u ф = u:
де ф-ція f (t - r / u) задовольняє одномерному хвильовому ур-нію. Однак в проміжній області, де kr
1, навіть в середовищі без дисперсії відбувається сильна деформація хвильового збурення (рис. 2).
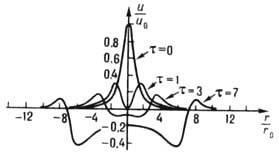
Мал. 2. Радиально розходиться циліндрична хвиля, задана в початковий момент часу в формі одиночного імпульсу u = u0 (1+ r / r0) 3/2. З увеліченіемt = ct / r0 (сростом часу t) імпульс розпливається, залишаючи за собою "шлейф".
Це пов'язано з тим, що Ц. в. в принципі нестаціонарна: віддаляючись від осі (центру), вона залишає за собою "шлейф", к-рий можна інтерпретувати як результат приходу хвильових збурень від все більш і більш віддалених від точки спостереження джерел на осі.
Літ. см. при ст. Хвилі. M. А. Міллер, Л. А. Островський.