1. Найпростіші методи обробки результатів багаторазових вимірювань.
2. Основні методи виявлення і усунення грубих і систематичних похибок.
3. Точкові та інтервальні оцінки розподілу випадкових похибок.
4. Нормування похибок і форми представлення результатів вимірювань.
5. Правила внесення поправок в результати вимірювань.
6. Оцінка похибки прямих і непрямих багаторазових вимірювань.
Найпростіші методи обробки результатів багаторазових вимірювань
Проводиться в такій послідовності:
1. Проводиться багаторазове вимір, в результаті якого отримуємо значення фізичної величини у вигляді:
2. Виключаємо систематичну помилку шляхом введення поправки
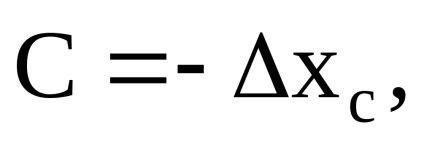
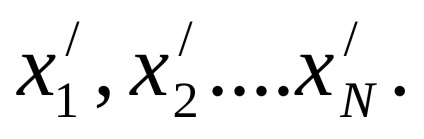
3. Обчислюємо середнє арифметичне значення
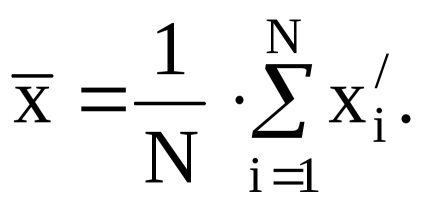
4. Обчислимо відхилення результату
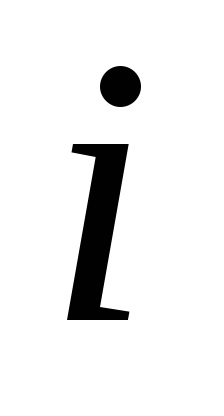
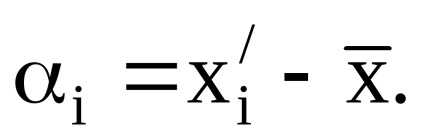
5. Обчислюємо СКО результату вимірювання
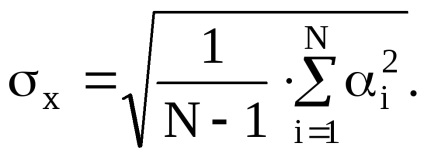
6. Оцінюємо нормальність результату (промах) спостережень. Для цього вибираємо найбільші відхилення і порівнюємо їх з СКО:
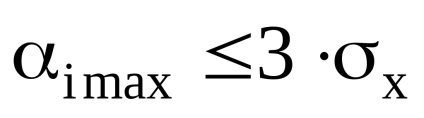
7. Якщо похибка вимірювання підпорядковуються закону Гаусса, то ймовірність появи похибки в межах кратного стандартного відхилення σх (довірчий інтервал ± σх. ± 2σх. ± 3σх):
Записуємо результат обчислень
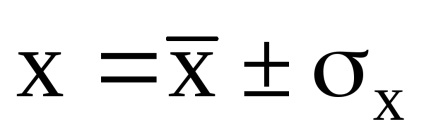
8. Якщо похибка вимірювання підпорядковуються закону Стьюдента, то СКО відхилення результату вимірювання:
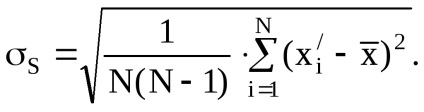
9. Обчислюємо довірчий інтервал ε, задаючись довірчою ймовірністю (наприклад Р = 0.95). За її значенням і кількістю вимірювань N попередньо по таблиці визначимо коефіцієнт Стьюдента - tS.
Значення коефіцієнта Стьюдента залежно від прийнятої довірчої ймовірності Р і числа результатів спостережень n по таблиці. Наприклад, для N = 4 і Р = 0,95 tS = 3,182; N = 5 при Р = 0,95 tS = 2,776; для N = 10 tS = 2,262; n = 15 tS = 2,145 при тій же Р = 0,95.
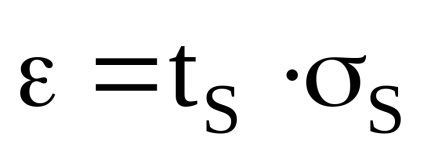
Записуємо результат обчислень.
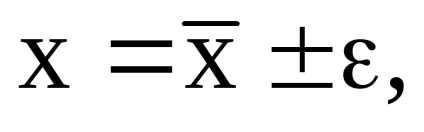
2. Основні методи виявлення і усунення грубих і систематичних похибок Виявлення та усунення грубих помилок (промахів)
Виявлення промахів необхідно провести до визначення похибок вимірювань. Ця операція особливо доцільна в тому випадку, якщо серед ряду вимірів зустрічаються окремі значення, різко відмінні від інших.
Промахи виникають, як правило, через невірні дії оператора, але можуть також бути результатом несправності використовуваних засобів вимірювань. У всіх випадках промахи не є характеристикою вимірювань, і для уникнення значних спотворень результатів їх необхідно відкинути.
Для об'єктивного вирішення питання про те, чи є промахом будь-якої результат вимірювання, застосовуються спеціальні методи. Найбільшого поширення набули два з них: метод (критерій) 3 і табличний метод (критерій Смирнова - Греббса).
В основу методу 3 ( «три сигма») належить припущення, що результати одноразових вимірювань
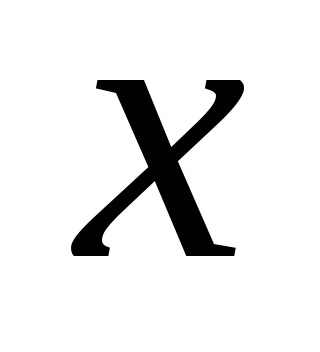
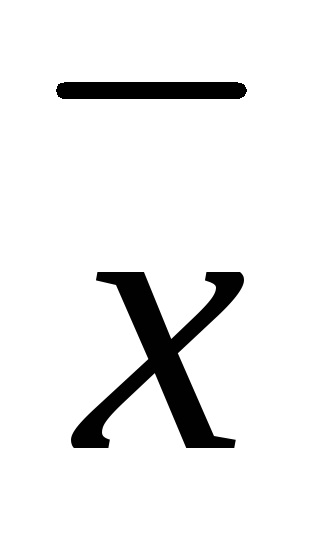
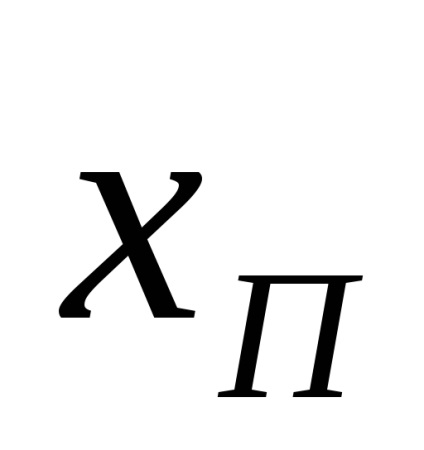
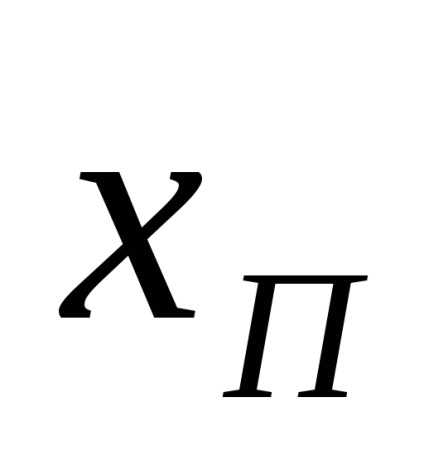
Метод 3 універсальний і може бути використаний при будь-якому законі розподілу розглянутих величин. Якщо закон розподілу розглянутих величин невідомий, то метод 3 формально застосуємо, але при цьому залишається невідомою довірча ймовірність, з якою виявляються промахи.
Для виявлення промахів за методом 3 необхідно виконати наступні операції:
підрахувати середнє арифметичне значення ряду вимірювань
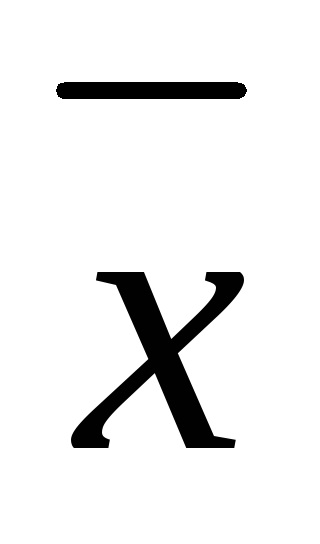
підрахувати середнє відхилення
знайти по абсолютній величині різниця А між передбачуваним промахом xп і середнім арифметичним значенням ряду вимірювань.
провести порівняння отриманої величини А з 3.
Якщо виконується умова А <3, то величина xп не является промахом.
Якщо умова А <3 не выполняется, то xП – промах и его следует отбросить.
Виявлення та усунення систематичних похибок
Систематичні похибки засобів вимірювань - це, як уже зазначалося вище, складові похибки, які в даному ряду вимірювань залишаються постійними або закономірно змінюються.
Слід зазначити, що систематичні похибки (як і випадкові) в різних точках шкали одного і того ж приладу або вимірювального пристрою можуть бути різні. Тому після проведення досліджень можна з упевненістю говорити про величину похибок лише в обраних точках шкали приладу. Що стосується інтервалів між точками, то тут зазвичай виходять із припущення, що від точки до точки похибки приладу змінюються плавно (без стрибків).
Оцінка систематичної похибки проводиться в наступній послідовності:
в кожній з обраних точок шкали приладу визначається середнє арифметичне значення
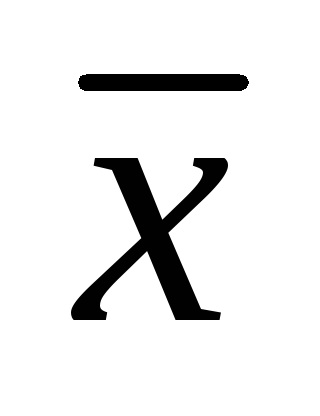
систематична похибка засобу вимірювань С визначається в кожній з обраних точок шкали як різниця між середнім арифметичним
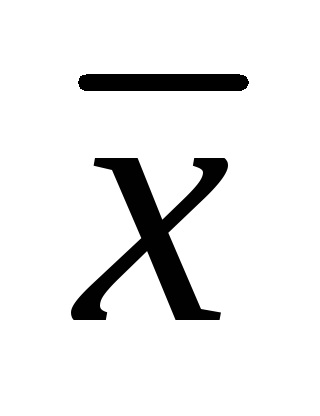
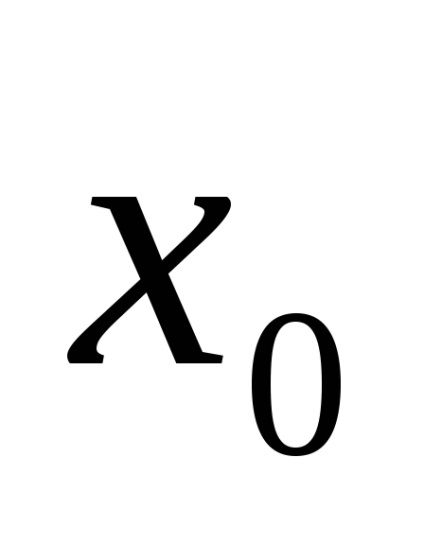
де - визначено вище.
Систематична похибка С може бути як позитивною (при
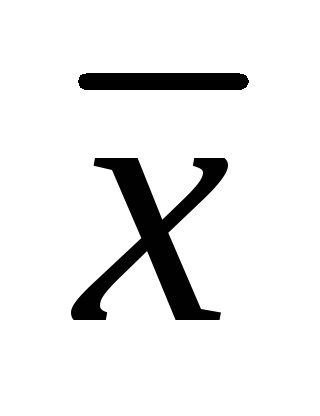
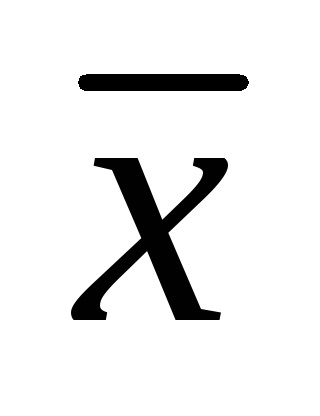
Істинне значення вимірюваної величини x0, як правило, невідомо, і замість x0 використовується дійсне значення вимірюваної величини, за яке приймають показання зразкових засобів вимірювань.
Систематична похибка, підрахована за формулою С =
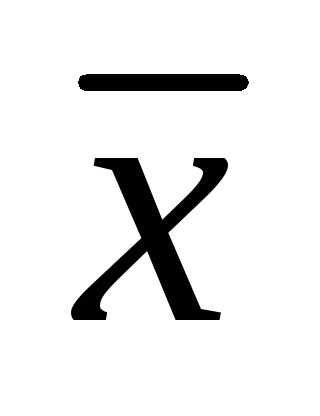
Крім абсолютних значень, підраховуються відносна С і наведена С систематичні похибки:
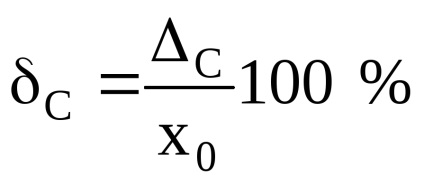
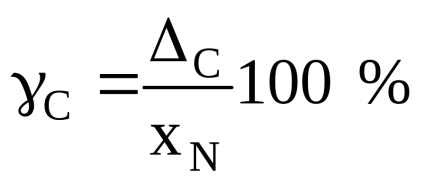
де xN - нормирующее значення (в більшості випадків ХN = Хk);
xK - верхня межа шкали приладу.
Відносна і приведена похибки виражаються зазвичай у відсотках, але можуть виражатися і у відносних величинах.
На рис. зображена числова вісь, на якій відкладено істинне значення вимірюваної величини x0 і нанесені результати вимірювань цієї величини досліджуваним засобом вимірювань. В результаті першого виміру отримано значення х1, другого - х2, третього - x3, і т. Д. (На рис. Позначені результати тільки перших чотирьох вимірювань). На числової осі відкладені також величини
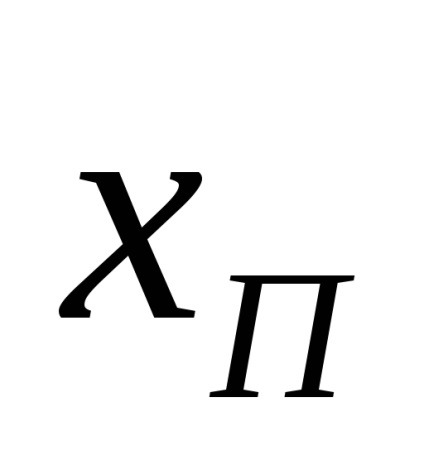
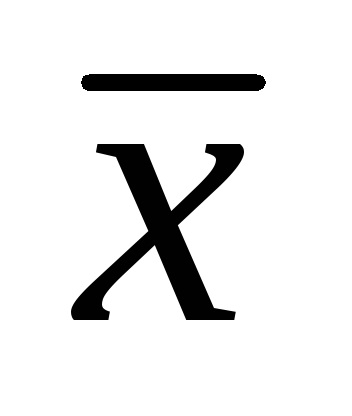

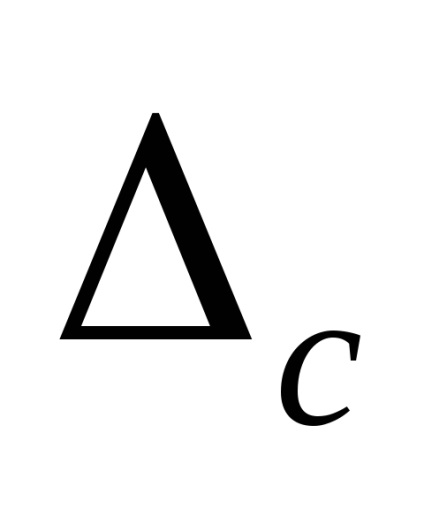


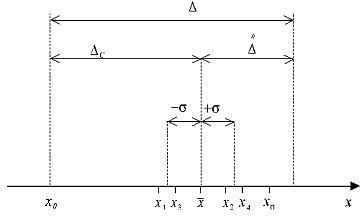
Мал. Графічна інтерпретація статичних похибок засобів вимірювань.
Таким чином, з наведеного рисунка випливає, що систематична похибка є деякою постійно присутньою середньою величиною, але аж ніяк не вичерпує всіх похибок вимірювального пристрою. Дійсно, різниця між результатами окремих вимірів і істинним значенням вимірюваної величини може перевершувати систематичну похибку (як, наприклад, різниці x2 -x0. X4-x0 і т.д.), тобто крім систематичної явно видно похибка випадкова.
Усунення систематичної похибки може бути досягнуто шляхом введення поправки в вимір, розмір якої дорівнює абсолютній величині систематичної похибки, а знак - зворотний знаку цієї похибки.
Для усунення постійних систематичних похибок застосовують такі методи:
Метод компенсації похибки за знаком. Цей метод застосовується для виключення відомих за своєю природою, але не відомих за значенням систематичних похибок. При цьому вимірювання проводять в два етапи, таким чином, щоб похибка входила в результат вимірювання з протилежними знаками. При першому вимірюванні результат записується у вигляді:
.
При другому вимірі.
Тоді, полусумма цих результатів буде вільна від систематичної похибки і результат вимірювання визначається як:
Таким способом усувають систематичну похибку від дії зовнішніх магнітних полів на вимірювальні механізми, зменшуються похибки в компараторах, мостових схемах і т.д.
Приклад. виміряти ЕРС за допомогою потенціометра постійного струму, що має паразитную термоЕРС. В результаті одного виміру отримуємо Е1. Потім, перемикаючи, полярність вимірюваної ЕРС, змінюємо напрямок робочого струму в потенціометрі і знову отримуємо результат Е2.
Метод протиставлення (зміни знака вихідної величини).
Він заснований на можливості змін вихідної величини при збереженні знака і величини систематичної похибки.
Цей метод використовується для компенсації систематичної похибки в СІ інтегруючого типу (наприклад, в цифрових вольтметра). Вимірювання так само проводять в два етапи.
Метод заміщення застосовується, якщо є регульована міра, вихідна величина якої однорідна із змінною величиною. Спочатку вимірюють невідому величину:
Потім до СІ підключають зразкову міру і з її допомогою встановлюють таке значення заходи, яке викликає таке ж показання індикатора СІ.
Різниця між значенням міри і показанням індикатора СІ свідчить про наявність систематичної похибки. Найбільш широко цей спосіб використовується при вимірюванні R, C і L, наприклад, за допомогою мостових схем змінного струму.
4. Метод повірки. Є загальним для виявлення систематичної похибки. Його суть полягає в порівнянні показань робочого і зразкового приладів. Систематична похибка визначається як різниця показань:
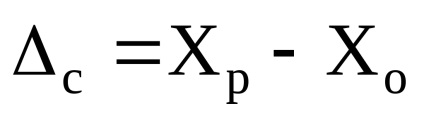
де Хр. Хо - результат вимірювання робочим СІ і зразковим СІ відповідно. Результати перевірки, тобто значення систематичної похибки є графік поправок:
Потім при проведенні вимірювань даним приладом систематичну похибку, відому за величиною і за знаком, виключають введенням поправки, числове значення якої дорівнює значенню систематичної похибки і протилежно по знаку. Поправка вводиться шляхом додавання її до результату вимірювання:
,
де ХД - виправлений результат вимірювання.
Новий результат вимірювання називається «виправленим».
Слід зазначити, що з застосуванням мікропроцесорної техніки і автоматизацією процесу вимірювань вдається автоматично проводити корекцію СІ і виключення систематичних похибок.
При проведенні вимірювань часто використовуються схемні методи корекції систематичних похибок. Компенсаційне включення перетворювачів, різні ланцюги температурної і частотної корекції є прикладами їх реалізації.
У тих випадках, коли причин систематичних похибок кілька, на основі наявних оцінок так званих «елементарних» систематичних похибок визначають сумарну систематичну похибку. При цьому кожну «елементарну» систематичну похибку розглядають як випадкову величину.