Прямі методи використовують деякі формули для обчислення невідомих величин за кінцеве число кроків обчислювального процесу
Приклад. Метод оберненої матриці
Істотним недоліком прямих методів є необхідність зберігання в пам'яті комп'ютера всіх n- квадратних елементів матриці системи, тобто прямі методи ніяким чином не враховують виряджену структуру матриці в системи.
Крім цього застосування прямих методів для вирішення СЛАР з великим числом змінних призводить до значного накопичення обчислювальних похибок.
До широко відомим методам відноситься метод Гаусса, метод прогонки.
Ітераційні методи (методи послідовних наближень) -це методи, в яких за допомогою будь-якого алгоритму будується ланцюжок наближених рішень
Кожен цикл таких обчислень називається итерацией.
Ітераційні алгоритми складніше прямих методів. Обсяг необхідних обчислень при їх використанні заздалегідь важко визначити, але вони не требуеют при роботі з вбраними матрицями зберігання всіх її елементів. Більш того, часто в них використовуються обчислювальні формули, що задають ці приклади. Ітераційний процес влаштований таким чином, що обчислювальні помилки від ітерації до ітерації не накопичуються. Тому ітераційний метод можна використовувати як для розв'язання добре обумовлених так і плохообусловленних СЛАР.
Приклади: Метод простої ітерації і метод Гаусса- Зейделя
Метод виключення Гаусса
Добре відомо, що алгоритм методу Гаусса для вирішення СЛАР складається з двох основних кроків.
На прямому ході шляхом послідовного виключення змінних з рівнянь системи, матрицю системи призводять до трикутного вигляду.
рішення методом виключення дає верхнетреугольную матрицю:
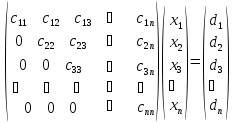
На зворотному ході обчислюється точне рішення системи
підставляємо в попереднє рівняння і отримуємо:
Метод Гаусса застосуємо ефективно лише в тому випадку, коли матриця системи добре обумовлена, має низьке число обумовленості.
Точність обчислення значно залежить від способу знаходження ведучого елемента, який ми використовуємо, для виключення змінних на прямому ході.
Приклад. Розглянемо систему:
Візьмемо в якості ведучого елемента
При вирішенні отримаємо:
якщо округлити, то приблизно отримаємо, що неправильно!
Тепер, візьмемо в якості ведучого елемента коефіцієнт перед з другого рівняння, тобто 1.
Тоді, якщо округлити, то отримаємо правильне рішення
Правила для вибору провідного елементу:
вибір за стовпцями
Розглядається перший стовпець. Передбачається, що ми хочемо виключити. Знаходимо в цьому стовпці максимальний елемент, тобто Знаходимо рівняння, де коефіцієнт присамая великий і переставляємо це рівняння на перше місце і використовуємо коефіцієнт прив якості ведучого елемента.
вибір по рядку
З першого рівняння знаходимо змінну, яку будемо виключати. Шукаємо і шукаємо відповідно, яке відповідає цьому максимальному елементу. І ставімна перше місце і виключаємо його.
Цю методику можна узагальнити на всі елементи
по всій матриці
Скануємо стовпці і рядки і шукаємо. Знаходимо, і ставимо цей елемент на перше місце.
Цей прийом найбільш прийнятний.
Метод прогонки є окремим випадком методу Гаусса, який спеціально призначений для вирішення систем рівнянь з розрядженою діагональною матрицею
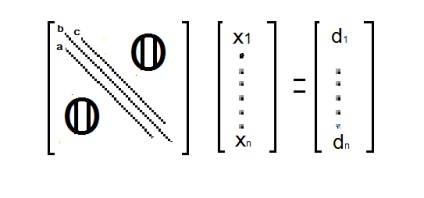
Прямий хід полягає в тому, що обчислюються коефіцієнти
Сам процес полягає в наступному.
Зворотній прогін відповідає обчисленню змінних в зворотному порядку, починаючи з самого останнього x
знаючи, можна знайти
У загальному випадку схема ітераційних методів розв'язання СЛАР полягає в наступному:
будь-яким стороннім способом потрібно встановити, будь-яке початкове рішення
обчислюємо праву частину:
знаходимо рішення системи рівнянь:, - вектор поправок
з 5. пункту йдемо у 2.
Важливим питанням є, коли потрібно зупинитися!
Як зупинки використовують будь-яке векторне нерівність, яке порівнює рішення, отримані на попередньої і наступної ітерації.