[Ред] Основна ідея
Візьмемо структуру даних динамічний масив. В її стандартної реалізації ми вміємо додавати елемент в кінець вектора, дізнаватися значення елемента, що стоїть на певній позиції, змінювати елемент по номеру і видаляти останній елемент. Припустимо, що нам необхідна структура даних з вищевказаними властивостями, а також з операціями: додати елемент в будь-яке місце (з відповідною зміною нумерації елементів) і видалити будь-який елемент (також з відповідною зміною нумерації). Таку структуру можна реалізувати на базі декартового дерева, результат часто називають декартово дерево по неявному ключу (англ. Treap with implicit key).
[Ред] Ключ X
Як відомо, декартово дерево - це структура даних, яка об'єднує в собі бінарне дерево пошуку і бінарну купу. При реалізації ж декартова дерева по неявному ключу модифікуємо цю структуру. А саме, залишимо в ньому тільки пріоритет, а замість ключа будемо використовувати наступну величину: кількість елементів в нашій структурі, що знаходяться лівіше нашого елементу. Інакше кажучи, будемо вважати ключем порядковий номер нашого елемента в дереві, зменшений на одиницю.
Зауважимо, що при цьому збережеться структура двійкового дерева пошуку по цьому ключу (тобто модифіковане декартово дерево так і залишиться декартових деревом). Однак, до цього підходу з'являється проблема: операції додавання і видалення елемента можуть поміняти нумерацію, і при наївною реалізації на зміну всіх ключів потрібно часу, де - кількість елементів в дереві.
[Ред] Допоміжна величина С
Вирішується ця проблема досить просто. Основна ідея полягає в тому, що такий ключ сам по собі ніде не зберігається. Замість нього будемо зберігати допоміжну величину: кількість вершин в поддереве нашої вершини (в поддерево включається і сама вершина). Звернемо увагу, що всі операції зі звичайним декартових деревом робилися зверху. Також зауважимо, що якщо по шляху від кореня до якоїсь вершини підсумувати все такі величини в лівих Піддерево, в які ми не пішли, збільшені на одиницю, то прийшовши в саму вершину і додавши до цієї величини кількість елементів в її лівому поддереве, ми отримаємо як раз її ключ.
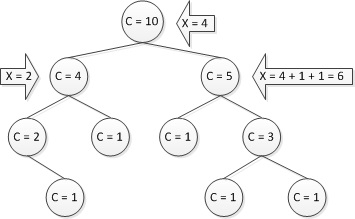
[Ред] Операції, що підтримують структуру декартова дерева
Структура звичайного декартова дерева підтримується за допомогою двох операцій: - розбиття одного декартова дерева на два таких, що в одному ключ менше, ніж задане значення, а в іншому - більше, і - злиття двох дерев, в одному з яких все ключі менше, ніж у другому. З урахуванням відмінностей декартова дерева по неявному ключу від звичайного, операції тепер будуть описуватися так: - розбиття дерева на два так, що в лівому виявиться рівно вершин, і - злиття двох будь-яких дерев, відповідно.
[Ред] Split
Нехай процедура запущена в корені дерева з вимогою відрізати від дерева вершин. Також відомо, що в лівому поддереве вершини знаходиться вершин, а в правому. Розглянемо всі можливі випадки:
- . В цьому випадку потрібно рекурсивно запустити процедуру від лівого сина з тим же параметром. При цьому новим лівим сином кореня стане права частина відповіді рекурсивної процедури, а правою частиною відповіді стане корінь.
- Випадок симетричний попереднього. Рекурсивно запустимо процедуру від правого сина з параметром. При цьому новим правим сином кореня стане ліва частина відповіді рекурсивної процедури, а лівою частиною відповіді стане корінь.
[Ред] Merge
Подивимося будь-яку з реалізацій процедури. Зауважимо, що в ній програма жодного разу не звертається до ключу. Тому реалізація процедури для декартова дерева по неявному ключу взагалі не буде відрізнятися від реалізації тієї ж процедури в звичайному декартовом дереві.
[Ред] Підтримка коректності значень C
Єдина дія, що забезпечує коректність цих значень полягає в тому, що після будь-якої дії з дітьми вершини потрібно записати в її поле суму цих значень в її нових дітей, збільшену на одиницю.
[Ред] Застосування описаного дерева
Таким чином, описана структура, від якої можна відрізати зліва частина довільної довжини і злити дві будь-які частини в одну в потрібному порядку. Тепер ми маємо можливість:
- вставити елемент в будь-яке місце (відріжемо потрібну кількість елементів зліва, сольем ліве дерево з деревом з одного доданого елемента і результат - з правим деревом),
- переставити будь-який шматок масиву куди завгодно (зробимо потрібні розрізи і злиття в правильному порядку),
- здійснювати групові операції з елементами. Згадаймо реалізацію таких операцій в дереві відрізків і зрозуміємо, що нічого не завадить нам зробити те ж саме з описаним деревом. У групові операції включається, природно, і взяття функції від відрізка,
- зробивши на одному вихідному масиві два дерева з елементів різної парності, можна вирішити задачу про зміну місць парних і непарних на відрізку,
- використовуючи ідеї декартова дерева по неявному ключу, можна реалізувати таку структуру даних як Rope.