Детермінована машина Тьюринга
Машина Тьюринга (МТ) - абстрактний виконавець (абстрактна обчислювальна машина). Була запропонована Аланом Тьюрингом в 1936 році для формалізації поняття алгоритму.
Машина Тьюринга є розширенням кінцевого автомата і, згідно з тезою Черча - Тьюринга. здатна імітувати всі інші виконавці (за допомогою завдання правил переходу), будь-яким чином реалізують процес покрокового обчислення, в якому кожен крок обчислення досить елементарний.
Пристрій машини Тьюринга
До складу машини Тьюрінга входить нескінченна в обидві сторони стрічка (можливі машини Тьюринга, які мають кілька нескінченних стрічок), розділена на осередки, і керуючий пристрій. здатне перебувати в одному з безлічі станів. Число можливих станів керуючого пристрою звичайно і точно задано.
Керуючий пристрій працює згідно з правилами переходу. які представляють алгоритм, реалізований цією машиною Тьюринга. Кожне правило переходу наказує машині, в залежності від поточного стану і спостережуваного в поточній клітці символу, записати в цю клітку новий символ, перейти в новий стан і переміститися на одну клітку вліво або вправо. Деякі стану машини Тьюринга можуть бути позначені як термінальні. і перехід в будь-який з них означає кінець роботи, зупинку алгоритму.
Машина Тьюринга називається детермінованою. якщо кожної комбінації стану і стрічкового символу в таблиці відповідає не більше одного правила. Якщо існує пара (стрічковий символ - стан), для якої існує 2 і більше команд, така машина Тьюринга називається недетермінованої.
Опис машини Тьюринга
Конкретна машина Тьюринга задається перерахуванням елементів безлічі букв алфавіту A, безлічі станів Q і набором правил, за якими працює машина. Вони мають вигляд: qi aj → qi1 aj1 dk (якщо головка знаходиться в стані qi. А в оглядається осередку записана буква aj. То головка переходить в стан qi1. В клітинку замість aj записується aj1. Головка робить рух dk. Яке має три варіанти: на осередок вліво (L), на осередок вправо (R), залишитися на місці (H)). Для кожної можливої конфігурації
Приклад машини Тьюринга
Наведемо приклад МТ для множення чисел в унарною системі числення. Машина працює за наступним набору правил:
У протоколі вказані початковий і кінцевий стани МТ, початкова конфігурація на стрічці і розташування головки машини (підкреслений символ).
Повнота по Тьюрингу
Можна сказати, що Машина Тьюринга являє собою найпростішу обчислювальну машину з лінійної пам'яттю, яка згідно формальним правилам перетворює вхідні дані за допомогою послідовності елементарних дій. Елементарність дій полягає в тому, що дія змінює лише невеликий шматочок даних в пам'яті (в разі Машини Тьюринга - лише одну клітинку), і число можливих дій звичайно. Незважаючи на простоту машини Тьюринга на ній можна обчислити все, що можна обчислити на будь-який інший машині, що здійснює обчислення за допомогою послідовності елементарних дій. Це властивість називається повнотою.
Один з природних способів докази того, що алгоритми обчислення, які можна реалізувати на одній машині, можна реалізувати і на інший, - це імітація першої машини на другий.
Як було сказано, на Машині Тьюринга можна імітувати (за допомогою завдання правил переходу) всі інші виконавці, яким-небудь чином реалізують процес покрокового обчислення, в якому кожен крок обчислення досить елементарний.
На Машині Тьюринга можна імітувати машину Посту. нормальні алгорифм Маркова і будь-яку програму для звичайних комп'ютерів, перетворюючу вхідні дані у вихідні з якого-небудь алгоритму. У свою чергу, на різних абстрактних виконавців можна імітувати Машину Тьюринга. Виконавці, для яких це можливо, називаються повними по Тьюрингу (Turing complete).
Є програми для звичайних комп'ютерів, що імітують роботу Машини Тьюринга. Але слід зазначити, що дана імітація неповна, так як в Машині Тьюринга присутній абстрактна нескінченна стрічка. Нескінченну стрічку з даними неможливо в повній мірі імітувати на комп'ютері з кінцевої пам'яттю (сумарна пам'ять комп'ютера - оперативна пам'ять, жорсткі диски, різні зовнішні носії даних, регістри і кеш процесора і ін. - може бути дуже великий, але, тим не менш, завжди кінцева).
Варіанти машини Тьюринга
Модель машини Тьюринга допускає розширення. Можна розглядати машини Тьюринга з довільним числом стрічок і багатовимірними стрічками з різними обмеженнями. Однак всі ці машини є повними по Тьюрингу і моделюються звичайною машиною Тьюринга
Машина Тьюринга, що працює на полубесконечной стрічці
Як приклад такого відомості розглянемо наступну теорему: Для будь-якої машини Тьюринга існує еквівалентна машина Тьюринга, що працює на полубесконечной стрічці.
Розглянемо доказ, наведене Ю.Г. Карповим в книзі «Теорія автоматів». Доказ цієї теореми конструктивне, тобто ми дамо алгоритм, за яким для будь-якої машини Тьюринга може бути побудована еквівалентна машина Тьюринга з оголошеним властивістю. По-перше довільно Занумеруем осередки робочої стрічки МТ, тобто визначимо нове розташування інформації на стрічці:
Потім перенумеруем осередки, причому будемо вважати, що символ "*" не міститься в словнику МТ:
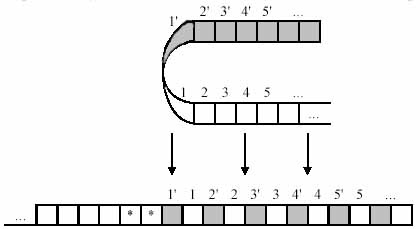
Нарешті, змінимо машину Тьюринга, подвоївши число її станів, і змінимо зрушення головки зчитування-запису так, щоб в одній групі станів робота машини була б еквівалентна її роботі в заштрихованої зоні, а в іншій групі станів машина працювала б так, як вихідна машина працює в незаштриховані зоні. Якщо при роботі МТ зустрінеться символ '*', значить головка зчитування-запису досягла межі зони:
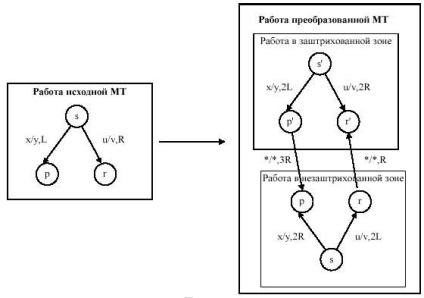
Початковий стан нової машини Тьюринга встановлюється в одній або іншій зоні в залежності від того, в якій частині вихідної стрічки розташовувалася головка зчитування-запису у вихідній конфігурації. Очевидно, що зліва від обмежують маркерів "*" стрічка в еквівалентній машині Тьюринга не використовується.