
Нижче подано деякі пояснення до матеріалів довідника. Курсивом виділено моя особиста думка, яке відрізняється від загальноприйнятого.
Для натуральних чисел визначено такі арифметичні дії. додавання, віднімання, множення, ділення, піднесення до степеня, добування кореня. Ніхто з математиків вам не пояснить, чим арифметичне додавання відрізняється від алгебраїчного додавання. Ті ж танці шаманів з бубнами. Євангеліє від Арифметики починається з арифметичного додавання, Євангеліє від Алгебри починається з алгебраїчного додавання. Це рівень сучасної математичної "науки".
Числа, які складаються, називаються доданки. Результат складання називається сума. Складові розрізняють по порядку їх запису в математичному вираженні: перший доданок, другий доданок і так далі. Ніхто з математиків не говорить про те, що складати можна тільки числа з однаковими одиницями вимірювання. До рівня одиниць виміру наші математики ще не доросли. Їх рівень - це дітлахи, які в пісочниці своїх визначень граються числами і не розуміють, що і як вони роблять.
Відніманням математики називають дію, зворотне додаванню. Число, з якого віднімають, називется уменьшамое. Число, яке віднімають, називется від'ємник. Результат віднімання називається різниця. Особисто я не виділяв би вічітаніе в окреме математичне дію, а розглядав його як елемент складання. Додавання - це зміна кількості розглянутої одиниці виміру. Математики байдуже, збільшується ця кількість або зменшується. Важливий тільки факт зміни.
Числа, які множаться, називаються співмножники. Результат множення називається приватне. Співмножники, як і складові, розрізняють по порядку запису в математичному вираженні: перший співмножник, другий співмножник і так далі. Чим відрізняється множення від додавання? При множенні змінюються одиниці виміру, при додаванні - немає. Видавати множення за багаторазове складання - це звичайне шахрайство. Скільки б відрізків ви не складали, вам ніколи не отримати площу. Скільки б разів ви не вимовляли слово "халва", в роті солодко не стане. Математика без одиниць виміру - це як людина без голови. Якщо ви будете вивчати поведінку людини, попередньо відриваючи людям голови, ви неминуче прийдете до висновку, що одяг робить всі дії і керує млявими тілами. До таких же результатів призводить вивчення чисел без одиниць виміру. Що ж стосується підміни множення складанням, то виглядає це так:
Деленіеем називається дію, зворотне множенню. Число, яке ділиться, називається ділене. Число, на яке ділять, називається дільник. Результат ділення називається приватне. У математиці прийнято вважати, що розподіл на нуль неможливо. Поділ не є математичним дією. Це рішення типової математичної задачі. Ділення дробів не існує, його математики підміняють множенням (знову шахрайство). В області чисел розподіл на нуль дейчтвітельно немає, але воно є в області одиниць виміру, які сучасна математика тупо ігнор.
Зведення в ступінь.
Множення однакових співмножників математики називають зведенням до степеня. Число, яке повторюється при множенні, називається підстава ступеня. Число сомножителей називається показник ступеня. Результат називається ступінь. Піднесення до степеня - це чергова типова задача, зведена в ранг математичних дій. Самі ж математики кажуть, що це множення.
Дія, зворотне зведення в ступінь, називається добування кореня. Результат зведення в ступінь називається підкореневе число. Показник ступеня називається показник кореня. Підстава ступеня називається корінь. Ще одна типова задача, названа математичним дією.
Примітки до математичних дій.
Дії додавання і множення мають властивості переместительности, асоціативної і розподільних. Слід зауважити, що віднімання, ділення, піднесення до степеня і добування кореня подібними властивостями не володіють саме тому, що вони не є математичними діями. Математичні властивості додавання і множення повинні виконуватися завжди і всюди, не залежно від розділів математики.
Вирази, за визначенням не мають сенсу: а / 0. де а ≠ 0 вважають не мають сенсу, так як результат ділення не існує; 0/0; 0 ° вважають не мають сенсу, оскільки результат відповідних дій не може бути визначений. Так говорить математичний довідник. Ось тут потрібно розібрати ситуацію більш детально.
Математики відносяться до своїх визначень так само, як релігійні віруючі ставляться до своїх Писанням - ні за яких обставин Писання не можна переписувати. Подібний підхід перетворює математику з науки в релігію, а самих математиків - в банальних релігійних проповідників. Єдина відмінність проповідників математики від проповідників релігії - вони самі пишуть свої Писання, в які потім змушують вірити всіх інших. Які правки потрібно внести в математику, щоб уникнути "виразів, які не мають сенсу" і нескінченного повторення "не дорівнює нулю"? Ось мої пропозиції.
Математика - це правила без винятків. Якщо в математичному правилі з'явилося виняток, значить це правило потрібно переглядати. Це універсальна формула для нових математичних відкриттів.
Нуль не є числом. У позиційній системі запису чисел нуль позначає відсутність числа певного розряду. Відсутність числа числом бути не може. Ввівши це правило в математику, математикам не потрібно буде постійно уточнювати, що число не дорівнює нулю в даному математичному вираженні.
Одиниці виміру - це такий же елемент математики, як і числа. Одиниці виміру надають всім математичних дій сенс, який неможливо побачити, розглядаючи виключно числа. Нуль - це відсутність даної одиниці вимірювання.
Ділення на нуль відбувається не в області чисел, а в області одиниць виміру. У позиційній системі запису чисел нуль позначає відсутність числа певного розряду. Відсутність числа числом бути не може. Ввівши це правило в математику, математикам не потрібно буде постійно уточнювати, що число не дорівнює нулю в даному математичному вираженні. Ось як виглядають правила поділу на нуль.
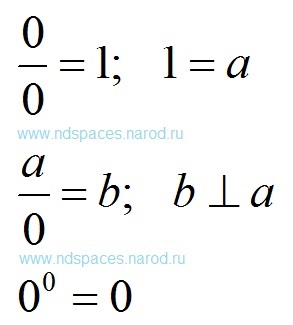
Нуль, поділений на нуль, дорівнює одиниці виміру. Це правило дозволяє вводити будь-які одиниці вимірювання. Протягом своєї історії людство постійно користувалося цим правилом, вводячи в ужиток найрізноманітніші різні одиниці вимірювання для самих різних речей. При цьому всі придумані одиниці виміру підпорядковувалися загальним математичним правилам.
Одиниця виміру, поділена на нуль, дорівнює перпендикулярній одиниці виміру. У математиці існує правило: будь-яке число, помножене на нуль, дорівнює нулю. Логічно припустити, що при розподілі числа на нуль будуть виникати все числа відразу. Всі числа об'єднуються однією одиницею виміру. Оскільки у діленого числа вже є своя одиниця виміру, то нова одиниця вимірювання може бути тільки перпендикулярна вже існуючої одиниці виміру. Дане правило ділення на нуль поширюється тільки на реальні одиниці виміру, що існують у природі. Віртуальні одиниці виміру, придумані нами, не підкоряються цьому правилу. Не можна уявити перпендикулярні долари, штуки, рази і так далі.
Нуль в ступеня нуль дорівнює нулю. Якщо нічого не зводити ні в яку ступінь, то результат буде відсутній. Відсутність результату прийнято позначати цифрою "нуль".
Скільки буде 0 помножити на 15? - Якщо 0 помножити на 15, то вийде 0.
0 * 15 = 0
3 помножити на нуль - 3 помножити на нуль дорівнює нулю.
3 * 0 = 0
Число поділити на 0. - Вчителям потрібно відповідати, що не можна число поділити на нуль, оскільки результат не існує.
Множення і ділення на 0. - Множення на 0 будь-якого числа дає в результаті 0, ділення на 0 неможливо.
Що виходити коли ми умнодаем на нуль? - У результаті виходить нуль.
Скільки буде два в першого ступеня? - Два в першого ступеня дорівнює двом.
Як виглядає натуральне число? - Натуральне число виглядає дуже навіть симпатично. Без хвостика (дрібна частина), без ріжків (показник ступеня), без черевця (знак мінус). На першій картинці все числа натуральні, можете милуватися.
Множення з нулем - У множенні з нулем немає нічого цікавого - в результаті завжди виходить нуль.
Правила з математики якщо будь-яке число помножити на нуль то буде нуль. - Абсолютно вірно, ви все правильно запам'ятали. Скільки років пройшло, коли ви це правило вчили?
Дивин вісім Поділ на сім. - Якщо дев'яносто вісім поділити на сім, вийде чотирнадцять.
98: 7 = 14
2 в квадраті дорівнює чотири.
2² = 2 * 2 = 4
3 в квадраті одно дев'ять.
3² = 3 * 3 = 9
12 в квадраті одно сто сорок чотири.
12² = 144
Два в четвертого ступеня одно шістнадцять. Немає у мене значка четвертого ступеня, тому я наведу приклад з множенням.
2 * 2 * 2 * 2 = 16
Квадрат числа 81 - Це шість тисяч п'ятсот шістдесят один.
81² = 6561
Якщо ж вас цікавить, квадрат якого числа дорівнює 81, тоді це дев'ять.
9² = 81
Таблиця компоненти при діленні - На першій картинці є така таблиця. Компоненти при розподілі - це ділене, дільник, приватне.
Зведення чисел в квадрат - Для зведення чисел в квадрат потрібно число помножити на точно таку саму кількість. Ось приклади.
2² = 2 * 2 = 4
3² = 3 * 3 = 9
11² = 11 * 11 = 121
0: а = 0. Хоча це вже не "Євангеліє від Арифметики", а "Євангеліє від Алгебри". Зараз не середньовіччя і математики мене на вогнищі НЕ спалять. Я так сподіваюся.
0: а = 0
Які цифри натуральні? - Цифри натуральними не бувають, натуральними бувають тільки числа. Цифри - це просто графічні символи, за допомогою яких ми записуємо числа. Визначення натуральних чисел можна прочитати на зображенні вгорі сторінки.