Динамічний розподіл пам'яті
Функція p = виділити (N) повертає покажчик на об'єкт пам'яті довжиною N,
У Сі - p = new (N) (невизначений тип покажчика).
1) Типізація покажчика.
В мови суворої типізації int * p і char * g - не еквівалентні => необхідно перетворення типу.
2) Звільнення виділеної пам'яті
· Явний механізм (програміст) - функція знищити (р);
· Ні явного механізму (ОС) - знищується, коли відсутні посилання на об'єкт, можна здійснювати через таймер, по завершенню программ, при переповненні.
3) Проблема висять об'єктів (коли один динамічний об'екс посилається на інший динамічний об'єкт)
В пам'яті залишаються об'єкти з відсутністю посилань. Знищивши цей об'єкт, можна втратити посилання на всі його подоб'екти.
4) Проблема висять покажчиків (остются посилання на знищені об'єкти);
5) Фрагментація пам'яті
Знищимо р3 і Р5 - на новий об'єкт вистачить пам'яті, але не буде цільного
Правила при роботі з динамічною пам'яттю при наявності явних механізмів знищення:
1) Не допускати наявність висячих об'єктів. Для цього спочатку треба знищити всі вкладені об'єкти.
2) Не допускати висять посилань, т. Е. Після знищення об'єкта знищити і посилання на нього - p = NULL.
3) Мінімізувати фрагментацію. Для цього потрібно знищувати об'єкти в порядку зворотному порядку їх створення: Р5 - р4 - р3.
Реалізація механізму динамічної пам'яті в C:
1) Виділення динамічної пам'яті через функцію void * malloc (size_t size).
Наприклад, якщо потрібно 10 елементів масиву, то:
Розмір необхідної пам'яті size_t size може бути більше, ніж потрібно (для вирівнювання)
2) Функція void * calloc (size_t num, size_t size);
всі значення в отриманої пам'яті нульові.
3) void free (void * p)
покажчик вказує на раніше захоплений блок пам'яті операціями malloc, calloc, realloc, т. е. число звільнених байтів = числу байтів, отриманих при захопленні
перетворення int в void free ((void *) A);
4) Функція void * realloc (void * p, size_t new size)
Змінює розмір раніше захопленого блоку пам'яті, p - покажчик на початок блоку, size - розмір в байтах. Блок може бути пересунутий в пам'яті при зміні розміру.
ДЕРЕВА. ВИЗНАЧЕННЯ, КЛАСИФІКАЦІЯ, СПОСОБИ ПРЕДСТАВЛЕННЯ.
Дерево з базовим типом Т - це:
1) Або порожнє дерево
2) Або вершина типу Т з кінцевим числом пов'язаних з нею окремих дерев з базовим типом Т (піддерева).
(Дерево, на яке посилається будь-яка вершина - поддерево)
Вершина, на яку безпосередньо посилається інша вершина - її нащадок. Зворотній вершина - предок.
Вершина, у якій немає нащадків - лист дерева.
Якщо пронумеруємо вершини так, щоб кожен наступний нащадок був на рівень вище, то вершина, яка перебуває на 0 рівні - корінь дерева.
Вершина, яка не є листом - внутрішня вершина.
Рівень будь-якої вершини - глибина (висота). а глибина самого дерева - максимальна глибина з усіх її вершин.
Кількість безпосередніх нащадків вершини називається ступенем даної вершини, ступінь дерева - максимальна з усіх можливих ступенів.
Число гілок (ребер), які необхідно пройти від кореня до вершини х, називається довжиною шляху до х (корінь має шлях 0).
Довжина шляху всього дерева (довжина внутрішнього шляху) - сума довжин шляхів до всіх його вершин.
Середня довжина шляху визначається за формулою:.
Дерево називається впорядкованим. якщо всі гілки, що виходять з будь-якої вершини, також є впорядкованими.
Впорядковані дерева другого ступеня називаються двійковими деревами.
Дерева n-ної (більшою 2) ступеня називаються сильно розгалуженим.
Дерева, які мають мінімальну висоту, називаються ідеально збалансованими (кількість вершин в лівому і правому поддереве відрізняються не більше ніж на 1 - умова для всіх вершин).
Вираз таких рекурсивних структур вимагає використання посилань.
Існує безліч різних способів подання дерев (на прикладі бінарного дерева):
1) Списочное уявлення бінарних дерев засноване на елементах, відповідних вузлів дерева. Кожен елемент має поле даних і два поля покажчиків. Один покажчик використовується для зв'язування елемента з правим нащадком, а інший - з лівим. Листя мають порожні покажчики нащадків. При такому способі подання дерева обов'язково слід зберігати покажчик на вузол, який є коренем дерева.
Можна помітити, що такий спосіб представлення має схожість з простими лінійними списками. І ця подібність не випадково. Насправді розглянутий спосіб представлення бінарного дерева є різновидом мультіспіска, утвореного комбінацією безлічі лінійних списків. Кожен лінійний список об'єднує вузли, що входять в шлях від кореня дерева до одного з листів.
struct binary_tree * left;
struct binary_tree * right;
Тоді порожнє дерево просто визначається установкою змінної Root в нульове значення:
Root = NULL;
2) У вигляді масиву найпростіше представляється повне бінарне дерево, так як воно завжди має чітко визначена кількість вершин на кожному рівні. Вершини можна пронумерувати зліва направо послідовно за рівнями і використовувати ці номери в якості індексів в одновимірному масиві.
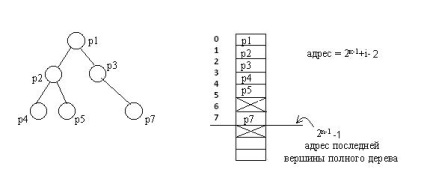
Якщо число рівнів дерева в процесі обробки не буде істотно змінюватися, то такий спосіб представлення повного бінарного дерева буде значно економічнішим, ніж будь-яка спискові структура.
Головним недоліком розглянутого способу представлення бінарного дерева є те, що структура даних є статичною. Розмір масиву вибирається виходячи з максимально можливої кількості рівнів бінарного дерева. Причому чим менше повним є дерево, тим менш раціонально використовується пам'ять.
Двійкового дерева, ОПЕРАЦІЇ.
Двійкове дерево - кінцеве безліч елементів (вузлів), яке або порожня, або складається з кореня з двома окремими двійковими піддеревами, які називають лівим і правим піддерево кореня.
Для побудови двійкового дерева з n вершинами, що має мінімальну висоту, використовуються наступні правила:
0) Якщо n = 0, то кінець;
1) Побудувати вершину
2) Побудувати ліве піддерево з вершинами;
3) Побудувати праве піддерево з вершинами.
Операції з двійковими деревами:
· Префіксний обхід - вершина, ліве, праве (+ ab):
prefix_walk (struct binary_tree * t)
· Інфіксне обхід - ліве, вершина, праве (a + b);
· Постфіксний - ліве, праве, вершина (ab +);
При використанні в цілях пошуку елементів даних за значенням унікального ключа застосовуються двійкові дерева пошуку дерево пошуку - все вершини в правому поддереве> x (вершина), все вершини в лівому поддереве
N елементів можна організувати в бінарне дерево з висотою не більше log2 (N). тому для пошуку серед N елементів може знадобитися не більше log2 (N) порівнянь, якщо дерево ідеально збалансовано. Звідси випливає, що дерево - це найбільш підходяща структура для організації пошуку, ніж, наприклад, лінійний список.