Увага! Даний сайт не оновлюється. Нова версія: shatalov.su
-
Попередні уроки:
- Координатні простору. Перейти.
- Перетворення координатних просторів. Перейти.
-
подальші уроки
- Рух у просторі і обертання навколо довільної прямої. Перейти.
Сьогодні ми більш детально розглянемо пристрій віртуальної камери. Почнемо з картинки.
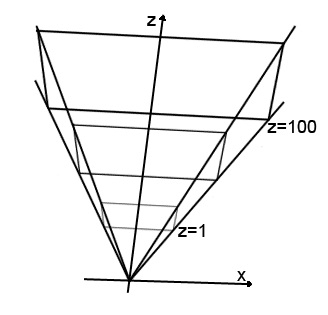
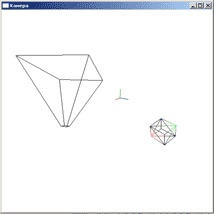
На малюнку ми бачимо координатне простір камери. Напрямок ( "погляд") камери завжди збігається з позитивним напрямком осі z, а сама камера розташована на початку координат.
Внутрішній простір піраміди зображеної на малюнку - це та частина віртуального світу, яку побачить користувач.
Зверніть увагу на три площини. Перша розташована на відстані 1 по осі z. Це ближня площину. Те що знаходиться до неї гравець ніколи не побачить. В даному випадку значення z дорівнює одиниці, але взагалі кажучи, воно може бути будь-яким. Саме з ближньої площиною пов'язаний один дефект відображення графіки. Цей дефект проявляється насамперед у шутерах (через великий свободи камери). Коли ти занадто близько підходиш до об'єкту, то можна опинитися "всередині". З останніх ігор цей дефект особливо сильно проявлявся в Left 4 dead: коли на гравця налягала юрба зомбі, то дуже часто можна було зазирнути всередину інших персонажів.
Площина розташована на відстані 100 одиниць по осі z називається далекої. Знову ж таки, значення може бути довільним. Користувач ніколи не побачить об'єкти розташовані далі цій площині.
Шість площин обмежують простір, яке побачить користувач, називаються відсікають (clipping planes): ліва права верхня нижня ближня і далека.
Площина розташована між ближньою і дальньою - проекційна. Надалі, цю площину ми будемо мати у своєму розпорядженні в z = 1, тобто вона буде збігатися з ближньої. Тут я відділив ближню і проекційну площині, щоб показати, що це все-таки не одне і те ж. Проекційна площина призначена для останнього перетворення координат: перетворення з тривимірного простору камери - в двомірне простір.
Саме завдяки проекційної площини користувач побачить віртуальний світ. Власне, ця площину і є те, що побачить користувач. Проекційна площина безпосередньо пов'язана з такими поняттями як основний / фоновий буфери, вікно програми і екран користувача. Всі ці поняття можна розглядати як прямокутну картинку, яка в пам'яті комп'ютера представлена масивом цифр.
Перетворення координат з тривимірного світу в проекційну площину - найскладніше з тих, які на даний момент були нами вивчені.
Поле зору / зона огляду (field of view)
На малюнку вище у проекційної площини (а значить і у зображення, яке побачить користувач) ширина більше висоти. Ширина і висота проекційної площини задаються за допомогою кутів. Зустрічаються різні назви цих кутів: поля зору або зони огляду. В англійському - fields of view.
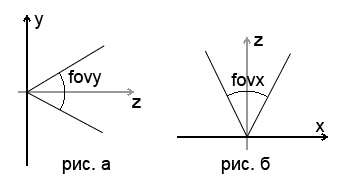
Зони огляду задаються двома кутами. Назвемо їх: fovx - зона огляду по горизонталі, fovy - зона огляду по вертикалі. Детально про зонах огляду: нижче.
Z-буфер / w-буфер / буфер глибини (z-buffer / w-buffer / depth buffer)
Подивимося на картинку, на якій представлено два трикутника: на відстані в 25 і 50 одиниць від камери. На малюнку (а) показано розташування трикутників в просторі (вид зверху), а на малюнку (б) можна побачити кінцеве зображення:
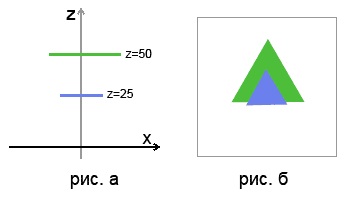
Як ви можливо здогадуєтеся, зображення потрібно малювати починаючи з самих віддалених елементів і закінчуючи самими ближніми. Очевидне рішення: обчислити відстань від початку координат (від камери) до кожного об'єкта, а потім порівняти. У комп'ютерній графіці використовується трохи більш вдосконалений механізм. У цього механізму кілька назв: z-буфер, w-буфер, буфер глибини. Розмір z-буфера за кількістю елементів збігається з розміром фонового і основного буферів. В z-буфер заноситься z-компонента самого ближнього до камери об'єкта. В даному прикладі, там де синій трикутник перекриває зелений, в буфер глибини будуть занесені z-координати синього. Ми ще поговоримо про z-буферах більш детально в окремому уроці.
Ортографічна / паралельна проекція (orthographic / parallel projection)
Операція при якій відбувається зменшення розмірності простору (було тривимірний простір, стало двомірним) називається проекцією. Перш за все нас цікавить перспективна проекція, але сналача ми познайомимося з паралельної (parallel або orthographic projection).
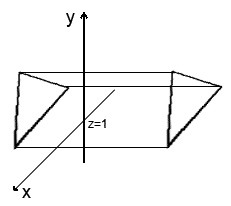
Для обчислення паралельної проекції досить відкинути зайву координату. Якщо у нас є точка в просторі [3 3 3], то при паралельній проекції на площину z = 1, вона спроецируется в точку [3 3 1].
Перспективна проекція (perspective projection) на проекційну площину
В даному виді проекції всі лінії сходяться в одній точці. Саме так влаштовано наш зір. І саме за допомогою перспективної проекції моделюється "погляд" у всіх іграх.
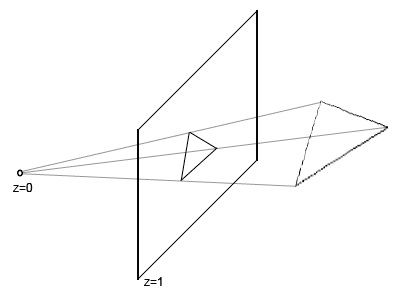
Порівняйте цей малюнок з малюнком показує однорідні координати з попереднього уроку. Щоб з тривимірного простору перейти в двомірне, потрібно перші дві компоненти векторів розділити на третю: [x / z y / z z / z] = [x / z y / z 1].
Як я вже писав вище, проекційна площина може розташовуватися де завгодно між ближньою і дальньою. Ми будемо завжди розміщувати проекційну площину в z = 1, але в цьому уроці ми розглянемо й інші варіанти. Подивимося на картинку:
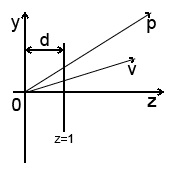
Відстань до проекційної площини від початку координат позначимо як d. Ми розглянемо два випадки: d = 1 і d = 5. Важливий момент: третій компонент всіх векторів після проекції повинна бути дорівнює d - всі крапки розташовані в одній площині z = d. Цього можна домогтися помноживши всі компоненти вектора на d: [xd / z yd / z zd / z]. При d = 1, ми отримаємо: [x / z y / z 1], саме ця формула використовувалася для перетворення однорідних координат.
Тепер, якщо ми відсунемо проекційну площину в точку z = 5 (соотвтественно d = 5), ми отримаємо: [xd / z yd / z zd / z] = [5x / z 5y / z 5]. Остання формула проектує всі вектори простору в одну площину, де d = 5.
У нас тут невелика проблемка. Попередня формула працює з тривимірними векторами. Але ми домовилися використовувати чотиривимірні вектори. Четверту компоненту в даному випадку можна просто відкинути. Але ми не будемо цього робити, так як її використання дає деякі специфічні можливості, які ми ще обговоримо.
Потрібно знайти спільний дільник третьої і четвертої компонент, при розподілі на який в третій компоненті залишається значення d, а в четвертій одиниця. Дільник цей - d / z. Тепер зі звичайного вектора [x y z 1] нам потрібно отримати вектор готовий до проекції (поділу) [x y z z / d]. Робиться це за допомогою матриці перетворення (перевірте результат помноживши будь-який вектор на дану матрицю):
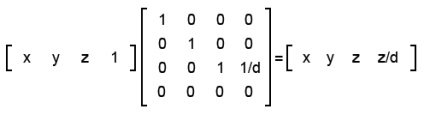
Останнє перетворення - це ще не проекція. Тут ми просто наводимо всі вектори до потрібної нам формі. Нагадую, що ми будемо розміщувати проекційну площину в d = 1, а значить вектори будуть виглядати ось так: [x y z z].
Матриця перспективного перетворення
Ми розглянемо матрицю перспективного перетворення використовується в DirectX:

Тепер ми знаємо для чого призначений елемент _34. Ми також знаємо, що елементи _11 і _22 масштабують зображення по горизонталі і вертикалі. Давайте подивимося, що конкретно ховається за іменами xScale і yScale.
Дані змінні залежать від зон огляду, про які ми говорили вище. Збільшуючи або зменшуючи ці кути, можна масштавбіровать (scale або zoom) зображення - змінювати розмір і співвідношення сторін проекційної площини. Механізм масштабування віддалено напомніает масштабування в фотоапаратах / камерах - принцип дуже схожий. Розглянемо малюнок:
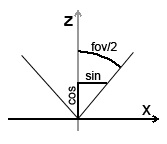
Розділимо кут fov на дві частини і розглянемо тільки одну половинку. Що ми тут бачимо: збільшуючи кут fov / 2 (а соответсвенно і кут fov), ми збільшуємо sin кута і зменшуємо cos. Це призводить до збільшення проекційної площини і відповідно до зменшення спроектованих об'єктів. Ідеальним для нас кутом буде fov / 2 = P / 4. Нагадую, що кут в P / 4 радіан дорівнює 45 градусам. При цьому fov буде дорівнює 90 градусам. Чим для нас хороший кут в 45 градусів? В даному випадку не відбувається масштабування, а cos (P / 4) / sin (P / 4) = 1.
Тепер ми можемо легко масштабувати картинку по вертикалі (горизонталі), використовуючи синус і косинус половини зони огляду (функція котангенс в C ++ називається cot):
В DirectX використовується тільки вертикальна зона огляду (fovY), а масштабування по горізонатлі залежить від вертикальної зони огляду і співвідношення сторін.
Нагадую, що вікно в наших програмах розміром в 500x500. Співвідношення сторін: 1 до 1. Тому змінні будуть рівні: xScale = 1, yScale = 1.
Співвідношення сторін стандартного монітора / телевізора: 4: 3. Цьому співвідношенню відповідають дозволу екрану: 640x480, 800x600, 1600x1200. Ми поки не будемо торкатися повноекранного режиму, але можемо змінити розмір вікна програми. Ви можете поміняти розмір вікна (в present parameters), наприклад, на 640X480. Але щоб все предмети не розтягнулися (квадрати будуть виглядати як прямокутники), не забудьте поміняти відповідні змінні в проекційної матриці.
Мало не забув, Форумули для xScale в DirectX:
Співвідношення сторін задаються просто: 1/1, 4/3, 16/9 - це зі стандартних.
Залишилося з'ясувати призначення елементів _33, _34 матриці перспективного перетворення. zf - z-координата далекої площині (від f ar - далеко), а zn - z-координата ближньої (від n ear - близько). Зверніть увагу, що елемент _43 = _33 * -zn.
Найлегше зрозуміти, що саме роблять ці формули, можна на прикладах. Помножимо стандартний вектор [x y z w] на матрицю представлену вище. Рекомендую вам зробити це, взявши аркуш паперу і олівець (сподіваюся ви пам'ятаєте як перемножать дві матриці). Компоненти вектора приймуть такий вигляд.
Зробимо проекційне перетворення (розділимо всі елементи на 4-у компоненту, при цьому допустимо, що d = 1 і w = 1):
В результаті ми отримали вектор виду:
Тепер, якщо ви задасте конкретні значення zf і zn, то виявите наступне (для позитивних значень): якщо вектор розташований до ближньої площини, то z-компонента після перетворення буде менше нуля, якщо вектор розташований за дальньої площиною, то z-компонента буде більше одиниці.
Немає ніякої разници де саме розташовані ближня і дальня площині: zn = 1, zf = 10 або zn = 10, а zf = 100 (або будь-які інші значення) - після перетворення видима область буде розташовуватися в відрізку від нуля до одиниці, включно.
Саме для цього і призначені формули в елементах _33, _34 проекційної матриці - спроектувати відстань від ближньої до дальньої площини в відрізок [0, 1]. Перевірте це, обчисливши значення декількох векторів для конкретних значень zn, zf (так-так, на листку паперу.).
Арканоід
Камера
клітини
спрайт
