Додавання паралельних сил

Знайдемо рівнодіюча двох діючих на тверде тіло паралельних сил в двох випадках:

1. Сили спрямовані в одну сторону.

Рівнодіюча двох діючих на абсолютно тверде тіло паралельних сил, спрямованих в одну сторону, дорівнює по модулю сумі модулів доданків сил, їм паралельна і спрямована в ту ж саму сторону. Лінія дії рівнодіючої проходить між точками програми доданків сил на відстанях від цих точок, назад пропорційних цим силам.

2. Сили спрямовані в різні боки.

Р

авнодействующая двох діючих на абсолютно тверде тіло паралельних сил, спрямованих в різні боки, дорівнює по модулю різниці модулів доданків сил, їм паралельна і спрямована в бік більшої сили. Лінія дії рівнодіючої проходить поза відрізка, що з'єднує точки докладання доданків сил, на відстанях від цих точок, назад пропорційних силам.

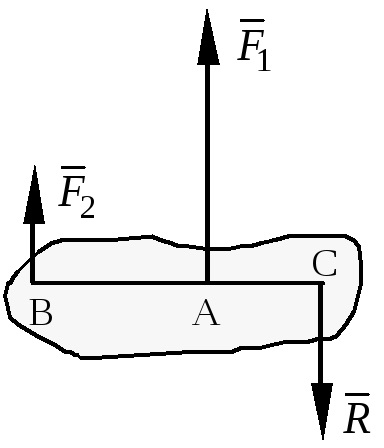
За допомогою наведених формул можна вирішувати завдання і про розкладанні сили на дві їй паралельні.

Пара сил - це система двох рівних по модулю, паралельних і направлених в протилежні сторони сил.

Площина, що проходить через лінії дії сил пари, називається площиною дії пари.

Відстань між лініями дії сил пари називається плечем пари.

П

ара сил не має рівнодійної. Дія пари на тіло зводиться до деякого обертального ефекту, чисельно що характеризується моментом пари сил.

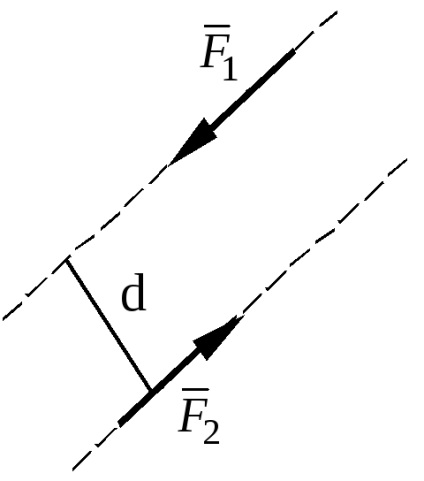
Моментом пари сил називається величина, що дорівнює взятому з відповідним знаком добутку модуля однієї з сили пари на її плече

Властивості пари сил

1. Дія пари сил на тіло не зміниться, якщо у неї довільним чином змінити сили і плече при незмінному моменті пари.

2. Не змінюючи дії пари сил, її можна переносити довільним чином в площині її дії.

3. Пару сил можна повернути в площині її дії на будь-який кут.

4. Дія декількох пар сил, прикладених в одній площині, можна замінити однією парою сил, момент якої дорівнює алгебраїчній сумі моментів заданих пар сил.

Умова рівноваги плоскої системи сил

Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на осі координат і алгебраїчна сума моментів всіх сил щодо будь-якої точки дорівнювали нулю

Теорема про паралельне перенесення сили

Теорема: Силу, прикладену до твердого тіла, можна, не змінюючи чиниться дії, переносити паралельно їй самій в будь-яку точку тіла, додаючи при цьому пару з моментом, рівним моменту яку переносять сили щодо точки, куди сила переноситься.

Приведення плоскої системи сил до заданого центру

Користуючись теоремою про паралельне перенесення, систему сил, що діє на тверде тіло, можна перенести в одну точку. Цю точку будемо називати центром приведення.

При цьому сила

,рівна геометричній сумі всіх сил системи, називаетсяглавним вектором системи. а величина, яка дорівнює сумі моментів всіх сил системи відносно центру пріведеніяO. називається головним моментом системи щодо центраO.

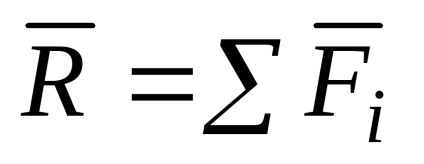
Теорема: Будь-яка плоска система сил, при приведенні до довільного центруOзаменяется однієї сілойR, рівній головному вектору системи, і яка додається в центрі приведення, і однією парою з моментомMO, рівним головному моменту системи щодо центраO.

Схожі статті

• Телепортація- переміщення через паралельні світи