\ (\ Blacktriangleright \) Функція \ (f (x) \) називається зростаючою на проміжку \ (X \). якщо для будь-яких \ (x_1, x_2 \ in X \). таких що \ (x_1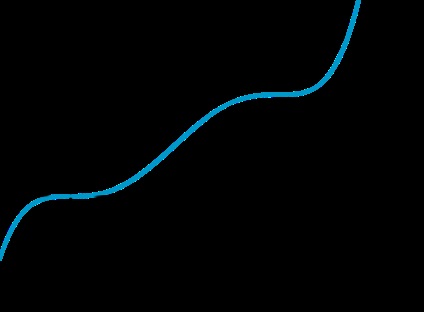
Функція називається неубивающей на проміжку \ (X \). якщо для будь-яких \ (x_1, x_2 \ in X \). таких що \ (x_1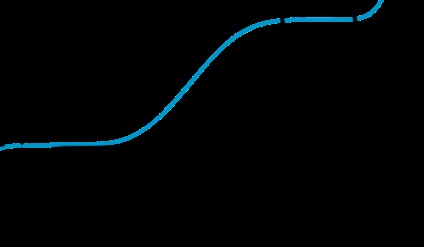
\ (\ Blacktriangleright \) Функція \ (f (x) \) називається спадною на проміжку \ (X \). якщо для будь-яких \ (x_1, x_2 \ in X \). таких що \ (x_1

Функція називається незростаюча на проміжку \ (X \). якщо для будь-яких \ (x_1, x_2 \ in X \). таких що \ (x_1
\ (\ Blacktriangleright \) Зростаючі і спадні функції називають строго монотонними. а незростаюча і неубутних - просто монотонними.
\ (\ Blacktriangleright \) Основні властивості:
I. Якщо функція \ (f (x) \) - строго монотонна на \ (X \). то з рівності \ (x_1 = x_2 \) (\ (x_1, x_2 \ in X \)) слід \ (f (x_1) = f (x_2) \). і навпаки.
Приклад: функція \ (f (x) = \ sqrt x \) є строго зростаючої при всіх \ (x \ in [0; + \ infty) \). тому з рівності \ (\ sqrt x = \ sqrt 4 \) слід \ (x = 4 \).
II. Якщо функція \ (f (x) \) - строго монотонна на \ (X \). то рівняння \ (f (x) = c \). де \ (c \) - деяке число, завжди має не більше одного рішення на \ (X \).
Приклад: функція \ (f (x) = x ^ 2 \) є строго спадною при всіх \ (x \ in (- \ infty; 0] \). Тому рівняння \ (x ^ 2 = 9 \) має на цьому проміжку не більше одного рішення, а точніше одне: \ (x = -3 \).
функція \ (f (x) = - \ dfrac 1 \) є строго зростаючої при всіх \ (x \ in (-1; + \ infty) \). тому рівняння \ (- \ dfrac 1 = 0 \) має на цьому проміжку не більше одного рішення, а точніше жодного, тому що чисельник лівої частини ніколи не може дорівнювати нулю.
III. Якщо функція \ (f (x) \) - неубутних (незростаюча) і неперервна на відрізку \ ([a; b] \). причому на кінцях відрізка вона приймає значення \ (f (a) = A, f (b) = B \). то при \ (C \ in [A; B] \) (\ (C \ in [B; A] \)) рівняння \ (f (x) = C \) завжди має хоча б одне рішення.
Приклад: функція \ (f (x) = x ^ 3 \) є строго зростаючою (тобто строго монотонної) і безперервної при всіх \ (x \ in \ mathbb \). тому при будь-якому \ (C \ in (- \ infty; + \ infty) \) рівняння \ (x ^ 3 = C \) має рівно одне рішення: \ (x = \ sqrt [3] \).
Перенесемо всі складові, що містять \ (ax \). вліво, а містять \ (x ^ 2 \) - вправо, і розглянемо функцію
\ [F (t) = 5 (t-2) ^ 3 + 15e ^ t + 6e ^ t \ cdot \ sin + 3e ^ t \ cdot \ cos \]
Тоді вихідне рівняння прийме вид:
\ [F (ax) = f (x ^ 2) \]
Знайдемо похідну:
\ [F '(t) = 15 (t-2) ^ 2 + 15e ^ t \ cdot (1+ \ cos) \]
Оскільки \ ((T-2) ^ 2 \ geqslant 0, \ e ^ t> 0, \ 1+ \ cos \ geqslant 0 \). то \ (f '(t) \ geqslant 0 \) при будь-яких \ (t \ in \ mathbb \).
Причому \ (f '(t) = 0 \). якщо \ ((t-2) ^ 2 = 0 \) і \ (1+ \ cos = 0 \) одночасно, що не виконується ні за яких \ (t \). Отже, \ (f '(t)> 0 \) при будь-яких \ (t \ in \ mathbb \).
Таким чином, функція \ (f (t) \) строго зростає при всіх \ (t \ in \ mathbb \).
Значить, рівняння \ (f (ax) = f (x ^ 2) \) рівносильне рівнянню \ (ax = x ^ 2 \).
Рівняння \ (x ^ 2-ax = 0 \) при \ (a = 0 \) має один корінь \ (x = 0 \). а при \ (a \ ne 0 \) має два різних кореня \ (x_1 = 0 \) і \ (x_2 = a \).
Отже, відповідь: \ (a \ in (- \ infty; 0) \ cup (0; + \ infty) \).
Рівень завдання: Рівний ЄДІ
Знайдіть всі значення параметра \ (a \). при кожному з яких рівняння \ [2 ^> \ cdot \ log _ >> + \ log_9 + 2)> = 0 \]
має єдине рішення.
Додати завдання в обране
Розглянемо функцію \ (y = 2 ^ t \ cdot \ log _> \) при \ (t \ geqslant 0 \) (тому що \ (\ sqrt \ geqslant 0 \)).
Похідна \ (y '= \ left (-2 ^ t \ cdot \ log_9 \ right)' = - \ dfrac \ cdot \ left (\ ln 2 \ cdot \ ln + \ dfrac \ right) \).
Оскільки \ (2 ^ t> 0, \ \ dfrac> 0, \ \ ln> 0 \) при всіх \ (t \ geqslant 0 \). то \ (y '<0\) при всех \(t\geqslant 0\).
Отже, при \ (t \ geqslant 0 \) функція \ (y \) монотонно убуває.
Рівняння можна розглядати у вигляді \ (y (t) = y (z) \). де \ (z = ax, t = \ sqrt \). З монотонності функції випливає, що рівність можливо тільки в тому випадку, якщо \ (t = z \).
Значить, рівняння рівносильне рівнянню: \ (ax = \ sqrt \). яке в свою чергу рівносильне системі: \ [\ begin a ^ 2x ^ 2x-1 = 0 \\ ax \ geqslant 0 \ end \]
При \ (a = 0 \) система має одне рішення \ (x = -1 \). яке задовольняє умові \ (ax \ geqslant 0 \).
Розглянемо випадок \ (a \ ne 0 \). Дискримінант першого рівняння системи \ (D = 1 + 4a ^ 2> 0 \) при всіх \ (a \). Отже, рівняння завжди має два кореня \ (x_1 \) і \ (x_2 \). причому вони різних знаків (тому що по теоремі Вієта \ (x_1 \ cdot x_2 = - \ dfrac<0\) ).
Це означає, що при \ (a<0\) условию \(ax\geqslant 0\) подходит отрицательный корень, при \(a>0 \) умові підходить позитивний корінь. Отже, система завжди має єдине рішення.
Значить, \ (a \ in \ mathbb \).
Розглянемо функцію \ (f (x) = 2x ^ 3-3x (ax + x-a ^ 2-1) -3a-a ^ 3 \) при деякому фіксованому \ (a \). Знайдемо її похідну: \ (f '(x) = 6x ^ 2-6ax-6x + 3a ^ 2 + 3 = 3 (x ^ 2-2ax + a ^ 2 + x ^ 2-2x + 1) = 3 (( xa) ^ 2 + (x-1) ^ 2) \).
Зауважимо, що \ (f '(x) \ geqslant 0 \) при всіх значеннях \ (x \) і \ (a \). причому дорівнює \ (0 \) тільки при \ (x = a = 1 \). Але при \ (a = 1 \):
\ (F '(x) = 6 (x-1) ^ 2 \ Rightarrow f (x) = 2 (x-1) ^ 3 \ Rightarrow \) рівняння \ (2 (x-1) ^ 3 = 0 \) має єдиний корінь \ (x = 1 \). що не задовольняє умові. Отже, \ (a \) не може дорівнювати \ (1 \).
Значить, при всіх \ (a \ ne 1 \) функція \ (f (x) \) є строго зростаючою, отже, рівняння \ (f (x) = 0 \) може мати не більше одного кореня. З огляду на властивості кубічної функції, графік \ (f (x) \) при деякому фіксованому \ (a \) буде виглядати наступним чином:

Значить, для того, щоб рівняння мало корінь з відрізка \ ([- 1; 0] \). необхідно: \ [\ begin f (0) \ geqslant 0 \\ f (-1) \ leqslant 0 \ end \ Rightarrow \ begin a (a ^ 2 + 3) \ leqslant 0 \\ (a + 2) (a ^ 2 + a + 4) \ geqslant 0 \ end \ Rightarrow \ begin a \ leqslant 0 \\ a \ geqslant -2 \ end \ Rightarrow -2 \ leqslant a \ leqslant 0 \]
Таким чином, \ (a \ in [-2; 0] \).
Рівень завдання: Рівний ЄДІ
Знайдіть всі значення параметра \ (a \). при кожному з яких рівняння \ [(\ sin ^ 2x-5 \ sin x-2a (\ sin x-3) +6) \ cdot (\ sqrt2a + 8x \ sqrt) = 0 \]
(Завдання від передплатників)
Додати завдання в обране
ОДЗ рівняння: \ (2x-2x ^ 2 \ geqslant 0 \ quad \ Leftrightarrow \ quad x \ in [0; 1] \). Отже, для того, щоб рівняння мало коріння, потрібно, щоб хоча б одне з рівнянь \ [\ sin ^ 2x-5 \ sin x-2a (\ sin x-3) + 6 = 0 \ quad >> \ quad \ sqrt2a + 8x \ sqrt = 0 \] мало рішення на ОДЗ.
1) Розглянемо перше рівняння \ [\ sin ^ 2x-5 \ sin x-2a (\ sin x-3) + 6 = 0 \ quad \ Leftrightarrow \ quad \ left [\ begin \ begin \ Sin x = 2a + 2 \\ \ Sin x = 3 \\ \ end \ end \ right. \ Quad \ Leftrightarrow \ quad \ sin x = 2a + 2 \] Дане рівняння повинно мати коріння на \ ([0; 1] \). Розглянемо коло:
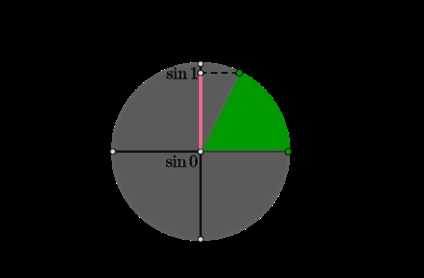
Таким чином, ми бачимо, що для будь-яких \ (2a + 2 \ in [\ sin 0; \ sin 1] \) рівняння матиме одне рішення, а для всіх інших - не матиме рішень. Отже, при \ (a \ in \ left [-1; -1+ \ sin 1 \ right] \) рівняння має рішення.
2) Розглянемо друге рівняння \ [\ sqrt2a + 8x \ sqrt = 0 \ quad \ Leftrightarrow \ quad 8x \ sqrt = -a \]
Розглянемо функцію \ (f (x) = 8x \ sqrt \). Знайдемо її похідну: \ [f '(x) = - 4 \ cdot \ dfrac> \] На ОДЗ похідна має один нуль: \ (x = \ frac34 \). який до того ж є точкою максимуму функції \ (f (x) \).
Зауважимо, що \ (f (0) = f (1) = 0 \). Значить, схематично графік \ (f (x) \) виглядає так:
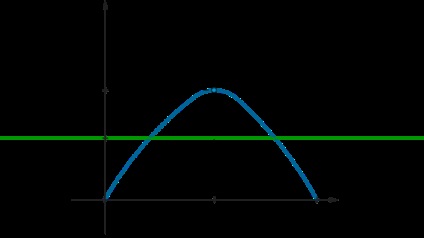
Отже, для того, щоб рівняння мало рішення, потрібно, щоб графік \ (f (x) \) перетинався з прямою \ (y = -a \) (на малюнку зображений один з відповідних варіантів). Тобто потрібно, щоб \ [0 \ leqslant -a \ leqslant f \ left (\ dfrac34 \ right) \ quad \ Rightarrow \ quad - \ dfrac2 \ leqslant a \ leqslant 0 \]
3) Таким чином, початкове рівняння матиме рішення при \ (a \ in \ left [-1; -1+ \ sin 1 \ right] \) або \ (a \ in \ left [- \ dfrac2; 0 \ right] \). Об'єднуючи ці рішення, отримаємо \ [a \ in \ left [- \ dfrac2; 0 \ right]. \]
Розглянемо сімейства функцій \ (f_a (x) = \ sqrt + 5x ^ 2-9x + 3a + 8, \ \ g_a (x) = \ dfrac \).
ОДЗ рівняння: \ (x \ geqslant 1 \). При цих \ (x \):
Функція \ (y_1 = \ sqrt \) є строго зростаючої. Графіком функції \ (y_2 = 5x ^ 2-9x \) є парабола, вершина якої знаходиться в точці \ (x = \ dfrac \). Отже, при всіх \ (x \ geqslant 1 \) функція \ (y_2 \) також строго зростає (права гілка параболи). Оскільки сума строго зростаючих функцій є строго зростаюча, то \ (f_a (x) \) - строго зростає (константа \ (3a + 8 \) не впливає на монотонність функції).
Функція \ (g_a (x) = \ dfrac \) при всіх \ (x \ geqslant 1 \) являє собою частину правої гілки гіперболи і є строго спадною.
Вирішити рівняння \ (f_a (x) = g_a (x) \) - значить знайти точки перетину функцій \ (f \) і \ (g \). З їх протилежної монотонності слід, що рівняння може мати не більше одного кореня.
При \ (x \ geqslant 1 \) \ (f_a (x) \ geqslant 3a + 4, \ \ \ 0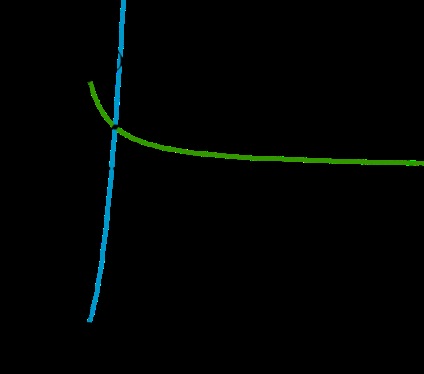
\ [3a + 4 \ leqslant a ^ 2 \ Rightarrow a \ in (- \ infty; -1] \ cup [4; + \ infty) \]