Досвід Боті найбільш безпосередньо підтверджує гіпотезу Ейнштейна про світлові кванти.
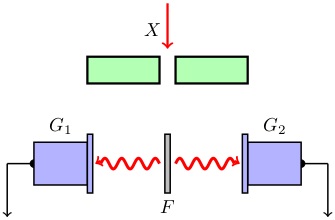
У цьому досвіді тонку металеву фольгу F встановлювали між двома швидко діючими лічильниками G1 і G2 (рис. 4). Фольгу опромінювали слабким пучком рентгенівського випромінювання X. під дією якого вона сама ставала джерелом рентгенівського випромінювання. Внаслідок досить слабкої інтенсивності первинного пучка кількість квантів, що випускаються фольгою, було досить мало.
Якби енергія цього випромінювання поширювалася у вигляді сферичних хвиль, то обидва лічильники повинні були б спрацьовувати одночасно. Досвід, однак, показав, що лічильники реагували абсолютно незалежно один від одного, і число збігів не перевищувало очікуваного числа випадкових збігів. Все відбувалося так, як якщо б випромінювання фольги F поширювалося у вигляді окремих квантів, які могли потрапляти або в один, або в інший лічильник.
Це можна пояснити лише тим, що в окремих актах випускання виникають кванти випромінювання, тобто частинки, що летять то в одному, то в іншому напрямку. Звичайно, була прийнята обережність від того, що в результаті первинного опромінення фольга випускала і електрони. Для виключення цього вікна лічильників мали таку товщину, щоб вони були здатні поглинути ці електрони і виключити їх вплив на результати досвіду.
Отже, експериментально було доведено існування особливих електромагнітних квантів, або фотонів. як їх згодом назвали.
Фотони. Розглянуті вище досліди і ряд інших з усією переконливістю підтвердили гіпотезу Ейнштейна про світлові кванти - фотони.
Світло частоти ω по Ейнштейну - це по суті потік фотонів з енергією. Світло поширюється у вакуумі зі швидкістю с. Значить з такою ж швидкістю поширюються і фотони. Відповідно до теорії відносності повна енергія Е будь-якої частинки, що рухається зі швидкістю v. визначається як
У разі фотона v = с. і знаменник цього виразу звертається в нуль. Для фотона, що має кінцеву енергію, це можливо лише за умови m = 0.
Таким чином, ми маємо справу з часткою, маса спокою якої дорівнює нулю.
Скориставшись зв'язком між енергією Е і імпульсом р рухається частинки, т. Е.
приходимо до висновку, що фотон (m = 0) має не тільки енергією, але і імпульсом
()
Ставлення ω / c = 2 π ν / c = 2 π / λ = k. де k - хвильове число, і тоді () набуде вигляду.
Таким чином, фотон як частка має енергію і імпульсом. Записавши імпульс у векторній формі, отримаємо остаточно для енергії і імпульсу фотона такі вирази:
де k - хвильовий вектор, модуль якого k = 2 π / λ.
Частота ω і хвильовий вектор k характеризують хвильові властивості монохроматичного світла, а енергія ε і імпульс р - корпускулярні.
Слід звернути увагу на те, що об'єкт, з яким ми познайомилися, фотон, як частка має досить своєрідні властивості. У нього відсутня маса (спокою), і його єдине стан - це рух з граничною швидкістю с. однаковою у всіх системах відліку. Не існує системи відліку, в якій він би спочивав. Фотон в стані спокою - поняття, позбавлене фізичного змісту. Спроба зупинити фотон або змінити напрямок його руху рівносильні його знищення. Такий вираз, як "фотон розсіявся на такий-то частці" широко використовують, але лише остільки, оскільки це не суперечить розгляду деяких явищ з енергетичної точки зору, і тільки.
Незважаючи на ці «дивацтва», фотон все ж зручно розглядати з тих же позицій, що і частинки, що мають масу. При цьому слід особливо підкреслити, що фотон не схожий на звичайну частку, лише деякі властивості фотона нагадують властивості частинки.