Дробове КРОКІВ МЕТОД
- метод побудови економічних (в сенсі числа операцій) стійких різницевих схем для вирішення диференціальних рівнянь математичного. фізики.
При збільшенні розмірності задачі число операцій для отримання чисельного рішення зростає як внаслідок зростання числа точок, так і внаслідок логічний. труднощів складання програми розрахунку. Для системи диференціальних рівнянь
де - диференційний оператор, і = і (х, t), x = (xt,. х п), абсолютно стійкі неявні схеми простий апроксимації
стають неефективними в разі багатовимірних задач. В одних випадках потрібно використовувати дуже дрібний крок за часом, в інших знаходження кожного un +1 вимагає constХN a (m) операцій, де N- число точок на один вимір, т-число просторових вимірів, а a (т) сильно зростає зі збільшенням т.
Для отримання економічних стійких різницевих схем запропоновані методи, засновані на наступних ідеях:
1) розщеплення різницевих схем;
2) наближеною факторизации;
3) розщеплення (слабкої апроксимації) диференціальних рівнянь.
У разі рівняння (1) відповідні різницеві схеми мають вигляд (для простоти взяті два дрібних кроку і розглядається периодич. Задача Коші): схема розщеплення:
схема наближеної факторизації:
схема слабкою апроксимації:
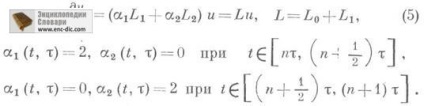
У разі схем (3) і (4) звернення оператора замінюється зверненням оператора т. Е. Послідовним зверненням операторів Е взагалі кажучи, більш простої структури.
Трактування (5) дозволяє розглядати схему розщеплення
як просту апроксимацію рівняння (5), слабо аппроксимирующего рівняння (1).
Таким чином, в основі цих методів лежить уявлення складних операторів через найпростіші, при цьому інтегрування вихідного рівняння зводиться до інтегрування рівнянь більш простої структури, а методи дрібних кроків повинні задовольняти умовам апроксимації і стійкості тільки в остаточному підсумку (при записі їх в "цілих" кроках ). Методом розщеплення вирішуються багато складні завдання математичного. фізики.
Велике розвиток отримали схеми розщеплення підвищеного порядку точності. До однієї з модифікацій методу розщеплення належить метод "частинок в осередках": тут розщеплення проводиться по фізичним процесам і не пов'язане зі зниженням розмірності операторів.
Літ. : [1] Яненко Н. Н. Метод дрібних кроків вирішення багатовимірних задач математичної фізики, Новосиб. 1967; [2] Самарський А. А. Введення в теорію різницевих схем, М. 1971.
Математична енциклопедія. - М. Радянська енциклопедія І. М. Виноградов 1977-1985