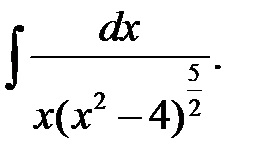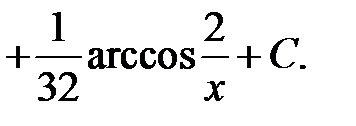Дрібно-лінійна підстановка

1). Якщо коріння в подинтегрального вираженні мають вигляд і т.д. де n, m, q, p, s, r і т.д. - натуральні числа, то воно перетворюється в раціональну дріб за допомогою підстановки. де k - найменше спільне кратне показників коренів і.

2). Якщо коріння в подинтегрального вираженні мають вигляд і т.д. n, m, q, p, s, r і т.д. - натуральні числа, то воно перетворюється в раціональну дріб за допомогою підстановки. де k - найменше спільне кратне показників коренів і

.

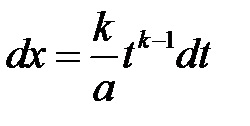
3). Якщо коріння в подинтегрального вираженні мають вигляд

. де n - натуральне число, то використовують підстановку . де

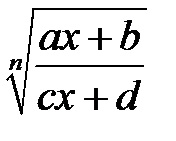
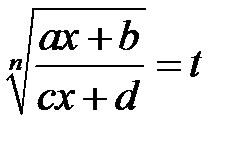
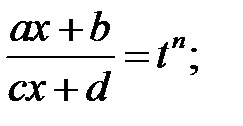
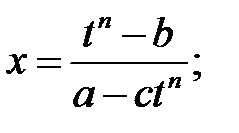
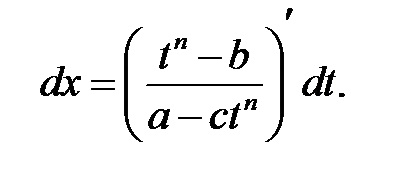
П р и м і р.Найті інтеграли: а)

б) ;

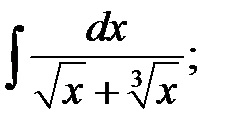
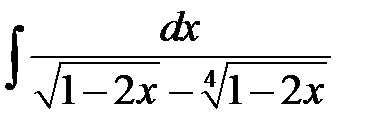
Р і ш е н і е. А) У подинтегрального вираженні є коріння другого і третього ступеня від х, тому робимо підстановку х = t 6. де 6 - найменше спільне кратне чисел 2 і 3.

7.2. Інтегрування иррациональностей за допомогою тригонометричних підстановок. Інтеграли виду після виділення під знаком радикала повного квадрата і використання лінійної підстановки

зводяться до інтегралів одного з наступних трьох типів: Після використання належної тригонометричної підстановки інтеграли цих трьох типів зводяться до інтегралів від функції, раціонально залежить від функцій sin x і cos x.

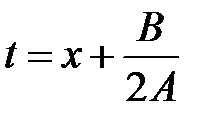
1. Інтеграл виду; підстановка

П р и м і р.Найті невизначений інтеграл.

Р і ш е н і е.Чтоби позбутися радикала, скористаємося підстановкою і зробимо заміну в невизначеному інтегралі

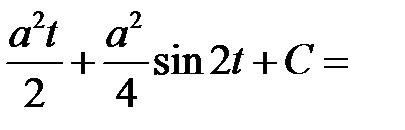
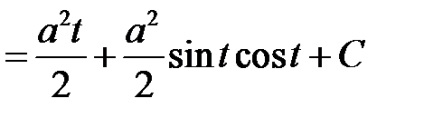
2. Інтеграл виду;

П р и м і р.Найті невизначений інтеграл

.

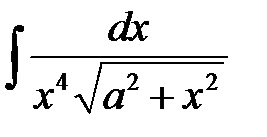
Р і ш е н і Е.С допомогою підстановки зведемо інтеграл від ірраціональної функції до раціональної щодо sin t.

=

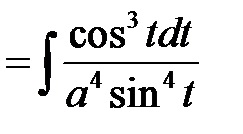
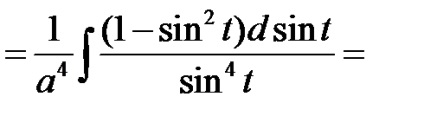
3. Інтеграл виду;

П р и м і р.Найті невизначений інтеграл