Згодом до репетитора з математики приходить майстерність пояснень складних понять простою мовою не на шкоду математичної повноті і точності. Виробляється індивідуальний стиль подачі матеріалу, мови, візуального супроводу та оформлення записів. Будь-який досвідчений репетитор розповість урок з закритими очима, бо наперед знає, які проблеми виникають з розумінням матеріалу і що потрібно для їх вирішення. Важливо підібрати правильні слова і записи, приклади для початку уроку, для середини і кінця, а також грамотно скласти вправи для домашнього завдання.
Про деякі приватних прийомах роботи з темою піде мова в даній статті.
З побудови яких графіків починає репетитор з математики?
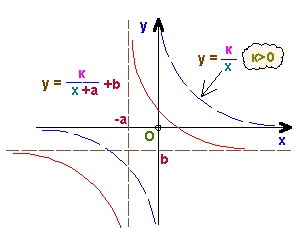
Потрібно почати з визначення досліджуваного поняття. Нагадую, що дробової лінійною функцією називають функцію виду. Її побудова зводиться до побудови самої звичайної гіперболи шляхом відомих нескладних прийомів перетворення графіків.
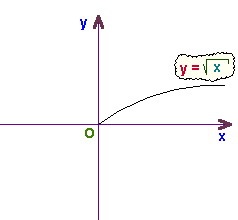
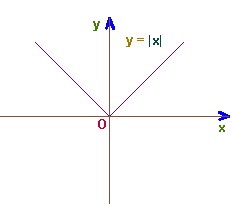
Отже, репетитора не залишається нічого зручнішого і ефективного, як провести підготовку до перетворень за допомогою квадратного кореня. Потрібна практика побудов графіків приблизно такого вигляду. Будемо вважати, що ця підготовка вдалася на славу. Дитина вміє зрушувати і навіть стискати / розтягувати графіки. Що далі?
Далі варто нагадати про те, як виглядає пряма пропорційність і в яких чвертях розташовується її графік в залежності від знака коефіцієнта k.
Наступний етап - навчання виділенню цілої частини. Мабуть, це основне завдання репетитора з математики, бо після того, як ціла частина буде виделенаона приймає на себе левову частку всієї обчислювальної навантаження на тему. Надзвичайно важливо підготувати функцію до виду, вписується в одну зі стандартних схем побудови. Також важливо описати логіку перетворень доступним зрозумілим. а з іншого боку математично точно і струнко.
Нагадаю, що для побудови графіка необхідно перетворити дріб до виду. Саме до такого, а не до
, зберігаючи знаменник. Чому? Складно виконувати перетворення того графіка, який не тільки складається з шматочків, але ще і має асимптоти. Безперервність використовується для того, щоб з'єднати дві-три більш-менш зрозуміло пересунути точки однією лінією. У разі розривної функції не відразу розбереш, які саме точки з'єднувати. Тому стискати або розтягувати гіперболу - вкрай незручно. Репетитор з математики просто зобов'язаний навчити школяра обходитися одними зрушеннями.
Для цього крім виділення цілої частини потрібно ще видалити в знаменнику коефіцієнт c.
Виділення цілої частини у дроби
Як навчити виділенню цілої частини? Репетитори з математики не завжди адекватно оцінюють рівень знань школяра і, незважаючи на відсутність в програмі докладного вивчення теореми про розподіл многочленів із залишком, застосовують правило ділення куточком. Якщо викладач береться за уголочное розподіл, то доведеться витратити на його пояснення (якщо звичайно все акуратно обґрунтовувати) майже половину заняття. На жаль, не завжди цей час у репетитора є в наявності. Краще взагалі не згадувати ні про які куточках.
Існує дві форми роботи з учнем:
1) Репетитор показує йому готовий алгоритм на якомусь прикладі дробової функції.
2) Викладач створює умови для логічного пошуку цього алгоритму.
Репетитор з математики вставляє пропуски для коефіцієнтів у вигляді порожніх прямокутників (як це часто використовують посібники для 5 - 6 класів) і ставить завдання - заповнити їх числами. Підбір слід вести зліва направо. починаючи з першого пропуску. Учень повинен уявити собі, як він буде розкривати дужку. Так як її розкриття вийде тільки один доданок з іксом, то саме його коефіцієнт повинен бути рівним старшому коефіцієнту в старому чисельнику 2х + 3. Тому, очевидно, що в першому квадратику виявляється число 2. Він заповнений. Репетитору з математики слід взяти досить просту дробову лінійну функцію, у якій з = 1. Тільки після цього можна переходити до розбору прикладів з неприємним видом чисельника і знаменника (в тому числі і з дробовими коефіцієнтами).
Йдемо далі. Викладач розкриває дужку і підписує результат прямо над нею.
Можна заштрихувати відповідну пару множників. До «розкритого доданку», необхідно додати таке число з другого пропуску, щоб отримати вільний коефіцієнт старого чисельника. Очевидно, що це 7.
Далі дріб розбивається на суму окремих дробів (зазвичай я обвожу дробу хмаркою, порівнюючи їх розташування з крильцями метелики). І кажу: «Розіб'ємо дріб метеликом». Школярі добре запам'ятали цю фразу.
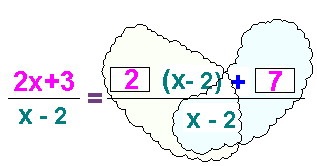
Репетитор з математики показує весь процес виділення цілої частини до виду, до якого вже можна застосувати алгоритм зсуву гіперболи:
Якщо знаменник має не дорівнює одиниці старший коефіцієнт, то ні в якому разі не потрібно його там залишати. Це принесе і репетитора і учня зайвий головний біль, пов'язану з необхідністю проведення додаткового перетворення, Причому найскладнішого: стиснення - розтягнення. Для схематичного побудови графіка прямої пропорційності не важливий вид чисельника. Головне знати його знак. Тоді до нього краще перекинути старший коефіцієнт знаменника. Наприклад, якщо ми працюємо з функцією, то просто винесемо 3 за дужку і «піднімемо» її в чисельник, конструюючи в ньому дріб. Отримаємо значно зручніше вираз для побудови: Чи залишиться зрушити на вправо і на 2 вгору.
Якщо між цілою частиною 2 і залишилася дробом виникає «мінус», його теж краще занести в чисельник. Інакше на певному етапі побудови доведеться додатково відображати гіперболу щодо осі Oy. Це тільки ускладнить процес.
Золоте правило репетитора з математики:
всі незручні коефіцієнти, що призводять до симетрія, до стисканням або розтягуванням графіка потрібно перекинути в чисельник.
Колпаков А.Н. Репетитор з математики Москва. Строгіно. Методики для репетиторів.