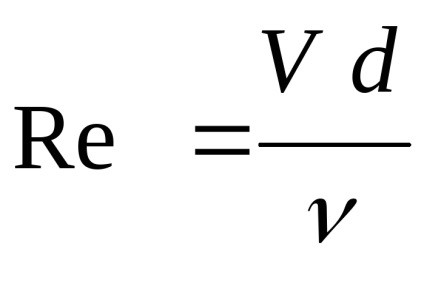Лекція 7. Режими течії рідин
Два режиму течії рідини
Фізичний сенс числа Рейнольдса
Основні особливості турбулентного режиму руху
Виникнення турбулентного течії рідини
Виникнення ламінарного режиму
Візьмемо прозору трубу, в якій з невеликою скоростьюV1 тече прозора рідина, наприклад, вода. У цей потік помістимо невеликі, істотно менші, ніж діаметр потоку, трубки. В трубках під напором знаходиться підфарбована рідина, наприклад, кольорові чорнила, яка може з них витікати, якщо відкрити крани До. Будемо відкривати їх на короткий час (1-3 секунди) і припиняти подачу чорнила через якісь проміжки часу так, щоб можна було простежити рух кольорової рідини. В такому випадку в потоці будуть виникати різнокольорові струмені, причому кольорова рідина буде явно показувати розподіл швидкостей (епюра швидкостей) по перетину потоку. Цей розподіл буде відповідати розглянутої раніше струменевого моделі потоку. Якщо спостерігати за рухом рідини, то можна ясно бачити, що при переміщенні від перетину 1 до перетину 2 картина розподілу швидкостей буде залишатися незмінною, а рух рідини буде шаруватим, плавним, все струмки струму будуть паралельні між собою. Такий рух носить назву ламинарное (від латинського слова lamina - шар).
Якщо збільшити швидкість основного потоку до велічіниV2 і повторити експеримент з кольоровими цівками, то епюри швидкостей як би витягнуться, а характер руху залишиться колишнім, ламінарним. Попутно зауважимо, що коефіцієнт кінетичної енергії α. що входить в рівняння Бернуллі і враховує ставлення дійсної кінетичної енергії потоку до кінетичної енергії, обчисленою з використанням середньої швидкості, при «витягуванні» епюри швидкостей зростає.
Якщо ще більше збільшити подачу рідини до скоростіV3. то епюри швидкостей можуть витягнутися ще більше і при цьому протягом буде спокійним, плавним - ламінарним. Коефіцієнт α наближається до значення 2.
Однак до нескінченності збільшувати швидкість при ламінарному режимі руху потоку неможливо. Обов'язково настане такий момент, коли характер руху рідини радикально зміниться. Кольорові цівки почнуть спочатку коливатися, потім розмиватися і інтенсивно перемішуватися. Перебіг потоку стає неспокійним, з постійним вихреобразование. Епюра розподілу швидкостей по перетину потоку наблизиться до прямокутної форми, а значення швидкостей в різних перетинах потоку стануть практично рівні середньої швидкості руху рідини. Значення коефіцієнта кінетичної енергііα наближається до 1.
Такий перебіг рідини називається турбулентним (від латинського слова turbulentus - обурений, безладний).
Якщо знову зменшити швидкість течії рідини, відновитися ламінарний режим руху. Перехід від одного режиму руху до іншого відбуватиметься приблизно при одній і тій же швидкості, яку називають критичною швидкістю і позначають Vкр. Експерименти показують, що значення цієї швидкості прямо пропорційно кінематичному коефіцієнту в'язкості рідини

У цих виразах коефіцієнти


безрозмірний коефіцієнт
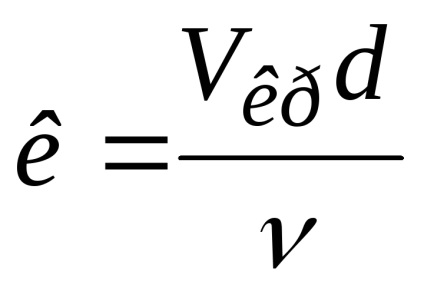
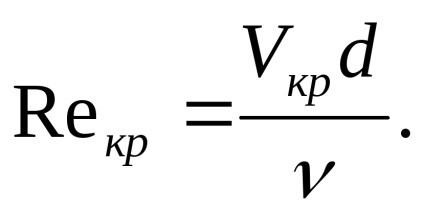
Дослідним шляхом встановлено, що критичне число Рейнольдса для круглих труб - 2320 для круглих труб, а для інших перерізів 580.
Для визначення режиму руху в потоці треба знайти фактичне число РейнольдсаRe. яке можна встановити для будь-якого потоку по формулі