Відповідно до принципів реалізації прінціпіальноий схеми по довільній таблиці істинності, розглянутими в попередніх розділах, отримаємо принципову схему суматора по модулю 2. Формування цієї схеми нічим не відрізняється від попередніх прикладів, розглянутих раніше. Як і раніше виділяємо рядка містять одиницю в вихідному сигналі. Вони реалізуються елементами "2И". Нульові потенціали вхідних сигналів в цих рядках перетворюються в поодинокі за допомогою інверторів. Об'єднання виходів логічних елементів в один виробляється логічним елементом "2ИЛИ". Отримана принципова схема суматора по модулю 2 приведена на малюнку 15.1.
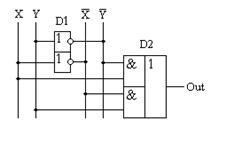
Малюнок 15.1 - Принципова схема, яка реалізує таблицю істинності суматора по модулю 2
Суматор за модулем 2 (для двох входів його схема повністю збігається зі схемою виключає "АБО") зображується на принципових схемах як показано на малюнку 15.2.
Малюнок 15.2 - Умовно-графічне позначення схеми, яка виконує логічну функцію "виключає АБО"
Суматор за модулем 2 виконує підсумовування без урахування перенесення між двійковими розрядами. У повному довічним сумматоре його необхідно враховувати, тому потрібні елементи, що дозволяють формувати перенесення в наступний двійковий розряд. Таблиця істинності такого пристрою, званого полусумматора, приведена в таблиці 15.2.
Зверніть увагу, що сигнали в наведеній таблиці істинності розташовані в порядку, прийнятому для схем, тобто відповідно до того, що сигнал поширюється зліва направо. В результаті перенесення, який має двійковий вага більший, в порівнянні з сумовною розрядами записаний правіше. У математиці прийнято інший порядок розрядів числа. Старший розряд на папері записується самим лівим, а молодший розряд записується самим правим. В результаті може виникнути плутанина. Щоб цього не сталося, приведу десятковий еквівалент кожного рядка таблиці істинності полусумматора (таблиця 15.2).
Перший рядок цієї таблиці істинності отримана з арифметичного виразу 0 + 0 = 010 (002). Другий рядок отримана з арифметичного виразу 0 + 1 = 110 (012). Третій рядок отримана з арифметичного виразу 1 + 0 = 110 (012). Четвертий рядок отримана з арифметичного виразу 1 + 1 = 210 (102).
Таблиця 15.2 - Таблиця істинності полусумматора
Відповідно до принципів побудови довільної таблиці істинності отримаємо принципову схему полусумматора. Схема, відповідна таблиці істинності, що міститься в таблиці 15.2, наведена на малюнку 15.3.
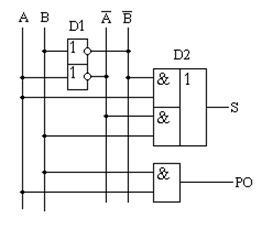
Малюнок 15.3 - Принципова схема цифрового пристрою, що реалізує таблицю істинності полусумматора
Полусумматора випускаються у вигляді окремих мікросхем і використовуються в якості окремих модулів в складі великих інтегральних мікросхем, тому ГОСТом передбачено умовно-графічне позначення полусумматора. Його приведено на малюнку 15.4.
Малюнок 15.4 - Умовно-графічне позначення полусумматора
Полусумматор формує перенесення в наступний розряд, але не може враховувати перенесення з попереднього розряду, тому він і називається полусумматора. В результаті такої особливості полусумматор не може використовуватися в якості окремого пристрою. Практичний інтерес представляє повний суматор.
Таблицю істинності повного однорозрядного довічного суматора (таблиця 15.3), як і таблицю істинності полусумматора, можна отримати з правил арифметичного підсумовування двійкових чисел. В позначенні входів і виходів повного суматора використано наступне правило: як входів використані однорозрядні двійкові числа A і B; сума - це однорозрядне двійковечисло S; перенос позначений буквою P; для позначення входу перенесення використовується поєднання букв PI (I - скорочення від англійського слова input, вхід); для позначення виходу перенесення використовується поєднання букв PO (O - скорочення від англійського слова output, вихід).
Таблиця 15.3 - Таблиця істинності повного двійкового
Тепер, точно так само як і в попередніх випадках, відповідно до правил побудови принципової схеми по довільній таблиці істинності отримаємо схему повного двійкового однорозрядного суматора. Схема, відповідна таблиці істинності, що міститься в таблиці 14.3, наведена на малюнку 15.5. Ця схема побудована з використанням СДНФ.
Малюнок 15.5 - Принципова схема, яка реалізує таблицю істинності повного двійкового однорозрядного сумматора
Схему повного однорозрядного суматора можна мінімізувати. Для цього достатньо подивитися на дві останні рядки його таблиці істинності. Ми можемо побачити, що сигнал перенесення в них не залежить від сигналу, присутнього на вході B. Тому цей вхід можна не заводити на вхід схеми "І".
В результаті описаних міркувань замість двох нижніх елементів "3І" можна скористатися одним двухвходових елементом "2И". Точно така ж ситуація виникає якщо розглянути рядки 6 і 8. У цьому випадку зайвим виявляється вхід A. Тобто і в цьому випадку можна обійтися одним двухвходових логічним елементом "2И".
Вхід PI виявляється зайвим у виразах, що описують рядки 4 і 8. В результаті описаних дій принципова схема формування переносу в наступний розряд суматора спрощується, і набуває вигляду, наведений на малюнку 15.6.
Малюнок 15.6 - Мінімізована принципова схема, яка реалізує таблицю істинності повного двійкового однорозрядного сумматора
Прикладом однорозрядного довічного суматора може служити мікросхема середньої інтеграції К155ІМ1. Умовно-графічне позначення повного двійкового однорозрядного сумматора показано на малюнку 15.7.
Малюнок 15.7 - Умовно-графічне зображення повного двійкового однорозрядного сумматора
Однак для виконання обчислень в схемах цифрової обробки сигналів недостатньо точності однорозрядного суматора. У них застосовуються 16- або навіть 40-розрядні двійкові суматори.
Для того щоб отримати багаторозрядних суматор з отриманого вище однорозрядного суматора, досить з'єднати входи і виходи переносів відповідних двійкових розрядів. Принципова схема чотирирозрядний суматора, реалізована на чотирьох однорозрядних суматорах, наведена на малюнку 15.8.
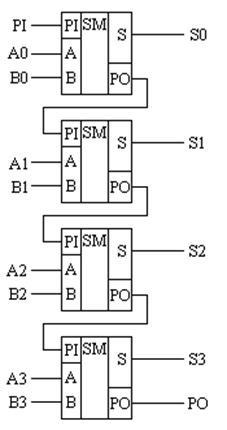
Малюнок 15.8 - Принципова схема чотирирозрядний двійкового суматора
На наведеній схемі двійковий вага розрядів сумміруемих чисел A і B відображений безпосередньо в назві ланцюга. Наприклад, ланцюг A0 передає нульовий розряд числа A, ланцюг B2 передає другий розряд числа B. Назви входу PI і виходу переносу PO не змінені.
Повний двійковий чотирьохрозрядний суматор зображується на схемах з використанням умовно-графічного позначення, показаного на малюнку 15.9. Зверніть увагу, що в цьому позначенні входи двійкового слова A об'єднані в окреме поле. Точно так же об'єднані входи двійкового слова B. Вхід і вихід сигналів перенесення на наведеному умовно-графічному позначенні мікросхеми теж виділені в окремі поля. Зображена таким чином мікросхема набагато більш наочно відображає свої функції.
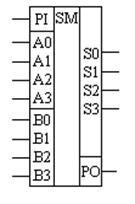
Малюнок 15.9 - Умовно-графічне позначення повного двійкового 4-розрядного суматора на схемах
Наведена на малюнку 15.8 схема не оптимізована за швидкодією, вона служить лише для пояснення принципу дії многоразрядного довічного суматора. У застосовуваних на практиці схемах ніколи не допускають послідовного поширення перенесення через все розряди многоразрядного суматора, так як це знижує його швидкодію.
Для збільшення швидкості роботи двійкового суматора використовується окрема схема формування переносів для кожного двійкового розряду. Таблицю істинності для такої схеми легко отримати з алгоритму підсумовування двійкових чисел, а потім застосувати добре відомі нам принципи побудови цифрового пристрою по довільній таблиці істинності.
Наступним, широко використовуваним в схемах цифрової обробки сигналів пристроєм, є цифровий двійковий помножувач. Ці пристрої використовуються як в схемах масштабування (підсилювачі або атенюатори) або гетеродінірованія сигналів, так і в складі цифрових фільтрів.