Основна властивість проективної площині - "симетрія" ролей, які грають точки і прямі в визначеннях і теоремах, і подвійність є формалізацією цієї концепції. Є два підходи до цієї подвійності: один, який використовує мову (див. "Принцип подвійності" нижче), і інший, більш функціональний підхід. Вони повністю еквівалентні і обидва служать вихідною точкою для аксіоматичних версій геометрії. У функціональному підході є відповідність між геометриями, яке називається подвійністю. У приватних прикладах таке відповідність може бути побудовано багатьма шляхами. Концепція подвійності площині легко розширюється до подвійності в будь-який конечномерной проективної геометрії.
Принцип подвійності [| ]
Якщо визначати проективну площину аксіоматично як структуру инцидентности в термінах безлічі точок P. безлічі прямих L і бінарного відношення інцидентності I. яке визначає, які точки лежать на яких прямих, то можна визначити подвійну структуру площині.
Якщо обміняти ролями "точки" і "прямі" в структурі инцидентности
отримаємо подвійну структуру
де I * - зворотне відношення [en] до I. C * є також проективної площиною, яка називається дуальної (двоїстої) площиною для C.
Якщо C і C * ізоморфні, то C називається самодвоїстих. Проективні площині PG (2, K) для будь-якого поля (або, в більш загальному випадку, для будь-якого кільця з розподілом, изоморфного двойственному йому) K є самодвоїстих. Зокрема, дезаргова площині кінцевого порядку завжди самодвоїстих. Однак серед недезаргових площин існують як самодвоїстих (наприклад, площини Хьюза [en]), так і не самодвоїстих (наприклад, площини Холла).
Для проективної площині твердження, що стосується точок, площин і їх инцидентности, отримане з іншого такого твердження шляхом обміну термінів "точка" і "пряма" (зі зміною, якщо потрібно, граматики), називається двоїстим твердженням. Двоїстим твердженням для "Через дві точки проходить єдина пряма" буде "Дві прямі перетинаються в одній точці". Освіта двоїстого затвердження називається дуалізації затвердження.
Якщо твердження вірне в проективної площині C, то подвійне твердження має бути вірним в дуальної площині C *. Це випливає з того, що дуализация кожного твердження в доказі "в C" дає твердження в доказі "в C *".
Принцип подвійності площині каже, що дуализация будь теореми в самодвоїстих проективної площині C породжує іншу вірну теорему в C.
Ця концепція може бути узагальнена до подвійності тривимірного простору, де поняття "точки" і "площині" міняються ролями (а прямі залишаються прямими). [1] Це призводить до Принципу двоїстості простору. Можливі й подальші узагальнення (дивіться нижче).
Ці принципи дають хороший привід для вживання "симетричного" терміна для відносини інцидентності. Так, замість пропозиції "точка лежить на прямій" можна сказати "точка і пряма інцидентні", і для дуалізації затвердження досить слова точка і пряма переставити місцями ( "пряма і точка інцідентни").
За визначенням проективна площину є безліч точок і прямих, і проективне перетворення може відображати точки на точки і прямі на прямі. Таке перетворення називається коллінеаціей. [2] При розгляді подвійності проективної площині розглядається інше відображення, при якому точки переходять в прямі, а прямі - в точки. Таке відображення називається кореляцією. [3] Проектне відображення визначається вимогами збереження
1) инцидентности точок і прямих 2) подвійного відносини [4]
Подвійні теореми [| ]
Оскільки матеріальна проективна площину PG (2, R) є самодвоїстих, існує ряд добре відомих тверджень, двоїстих одна одній. Серед них:
Двоїстість як відображення [| ]
Двоїстість (площині) - це відображення з проективної площині C = (P, L, I) в її дуальну C * = (L, P, I *), що зберігає властивість инцидентности. Таким чином, подвійність (площині) σ відображає точки в прямі і прямі в точки (P σ = L і L σ = P) таким чином, що якщо точка Q лежить на прямій m (позначається QI m), то Q σ I * m σ ⇔ m σ IQ σ. Двоїстість (площині), що є изоморфизмом, називається кореляцією. [5] Існування кореляції означає самодвоїстих проективної площині.
У спеціальному випадку, коли проектна площину має тип PG (2, K), де K - кільце з розподілом, подвійність називається взаємним перетворенням. [6] За фундаментальної теоремі проективної геометрії [en] взаємне перетворення є композицією Автоморфні функції на K і a проективного перетворення. Якщо використовуваний автоморфизм є тотожним, то взаємне перетворення називається проективної кореляцією.
Кореляція другого порядку (інволюція) називається полярітетом. Якщо кореляція не є полярітетом, то φ 2 буде нетривіальною коллінеаціей.
Ця концепція відображення може бути поширена і на простору вищих розмірностей, так що згадка площині може бути видалено.
Двоїстість високих розмірностей [| ]
Двоїстість проективної площині є спеціальним випадком подвійності для проективних просторів. перетворень PG (n, K) (які позначаються також KP n), де K - поле, які обмінюють об'єкти розмірності r з об'єктами розмірності n - 1 - r (= коразмірність r + 1). Таким чином, в проектному просторі розмірності n точки (розмірність 0) будуть відповідати гіперплоскостей (коразмірність 1), прямі, що проходять через дві точки (розмірність 1), будуть відповідати перетинанню двох гіперплоскостей (коразмірність 2), і так далі.
Точки PG (n, K) можна розглядати як ненульові вектора в (n + 1) -мірному векторному просторі над K. в якому ми ототожнюємо два вектора, якщо вони відрізняються лише множенням на скаляр. Інший спосіб представлення як точки n мірного проективного простору - як прямі, що проходять через початок координат в Kn + 1. які є 1-мірними векторними підпросторами. Отже, n -мірні векторні підпростору поля Kn + 1 представляють (n - 1) -мірні геометричні гиперплоскости проективних n -простору над K.
Ненульовий вектор u = (u0, u1. Un) в Kn + 1 визначає (n - 1) - мірне геометричне підпростір (гіперплоскость) Hu,
Вектор u. використовуваний для визначення гиперплоскости, позначимо uH. а для позначення точки, відповідної кінця вектора, будемо використовувати позначення uP. У термінах звичайного скалярного твори. Hu = xP: uH • xP = 0>. Оскільки K є полем, скалярний твір симетрично, що означає uH • xP = u0 x0 + u1 x1 +. + Un xn = x0 u0 + x1 u1 +. + Xn un = xH • uP. Можна задати взаємне перетворення uP ↔ Hu між точками і гіперплоскостямі. Це відповідність можна поширити на прямі, утворені двома точками і перетин двох гіперплоскостей, і так далі.
На проективної площині PG (2, K) з полем K ми маємо відповідність: однорідні координати (a, b, c) ↔ прямі, що задаються рівняннями ax + by + cz = 0. У проектному просторі PG (3, K) відповідність виглядає як точки в однорідних координатах (a, b, c, d) ↔ площині, що задаються рівняннями ax + by + cz + dw = 0. Це відповідність також відображає пряму, що задається двома точками (a1, b1, c1, d1) і (a2, b2, c2, d2), в пряму, яка є перетином двох площин, що задаються рівняннями a1 x + b1 y + c1 z + d1 w = 0 і a2 x + b2 y + c2 z + d2 w = 0.
Тривимірний простір [| ]
У полярних відображеннях речового проектованого 3-мірного простору PG (3, R) точки відповідають площинах, а прямі відповідають прямим. У стереометрії має місце подвійність багатогранників. коли точки двоїсті гранях, а ребра двоїсті ребрах, так що ікосаедр двоїстий додекаедрів. а куб двояко октаедру.
Геометричну побудову взаємної перетворення [| ]
Відповідність в PG (2, R) в однорідних координатах може бути описано геометрично. Для цього використовується модель речової проективної площині [en] "одинична сфера з ототожненням антиподів [7]", або, що еквівалентно, модель прямих і площин, що проходять через початок координат простору R 3. Порівняємо прямої, що проходить через початок координат єдиною ортогональної площині, містить початок координат. Якщо в цій моделі прямі вважати точками, а площині - прямими проективної площині PG (2, R), це зіставлення стає відповідністю (а фактично - полярним відображенням) проективної площині. Сферичну модель можна отримати як перетин прямих і площин, що проходять через початок координат з одиничною сферою, що має центр на початку координат. Прямі перетинають сферу в двох протилежних точках, які ототожнюються для отримання точки проективної площині, площині ж перетинають сферу по великим колам. які є прямими проективної площині.
Те, що таке зіставлення "зберігає" инцидентность, легко показати на моделі прямих і площин. Точка, инцидентная прямий в проективної площині, відповідає прямий, що на площині в моделі. Згідно порівнянні, площина стає прямою, що проходить через початок координат і перпендикулярній площині. Цей образ (пряма) перпендикулярна будь-якої прямої, що лежить на площині, а в тому числі і вихідної прямий (точки проективної площині). Всі прямі, перпендикулярні вихідної прямий, утворюють площину, яка є асоційованою площиною вихідної прямий. Таким чином, образ прямої лежить в образі площині, так що инцидентность збережена.
Полюса і поляри [| ]
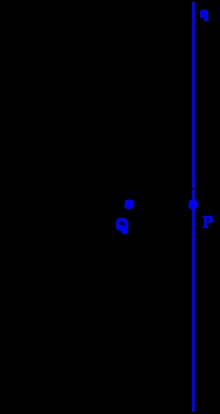
Полюс і поляра для окружності O. P = Q '. q - поляра для Q. Q - полюс для q.
В евклідовому просторі зафіксуємо окружність C з центром O і радіусом r. Для кожної точки P. відмінною від O. визначимо образ Q '. так що OP • OQ = r 2. Відображення P → Q називається інверсією [en] [8] щодо кола C. Пряма q. що проходить через P. перпендикулярна OP. називається полярою точки Q по відношенню до кола C.
Нехай q - пряма, що не проходить через O. Опустимо перпендикуляр з O на q. який перетинає q в точці P (це найближча до O точка прямої q). Образ точки Q (точка P) при інверсії відносно C називається полюсом прямій q. Якщо точка M лежить на прямій q (що не проходить через O), то полюс прямий q лежить на поляра точки M і навпаки. Процес, який зберігає инцидентность, при якому точки і прямі переходять в їх поляри і полюси, по відношенню до C називається проективним перетворенням. [9]
Щоб зробити цей процес взаємним перетворенням, евклидово простір (що не є проективної площиною) необхідно розширити до розширеної евклідової площині шляхом додавання прямий на нескінченності [en] і точок на нескінченності [en]. які лежать на цій нескінченно віддаленої прямий. На цій розширеній площині ми визначаємо поляра точки O як пряму на нескінченності (і O є полюсом на нескінченності), і полюси прямих, що проходять через O як точки на нескінченності, де, якщо пряма має кутовий коефіцієнт s (≠ 0), її полюс є нескінченно віддаленої точкою, що відповідає класу паралельних прямих з нахилом -1 / s. Полюс для осі x - це точка на нескінченності вертикальних прямих, а полюс осі y - точка на нескінченності горизонтальних прямих.
Побудова полярного перетворення для інверсії щодо кола, дане вище, можна узагальнити з використанням інверсії щодо конічних перетинів (на розширеній речової площині). Взаємне перетворення, побудоване таким чином, є проективної кореляцією другого порядку, тобто полярним перетворенням.
Відображення сфери в площину [| ]
Модель проективної площині з одиничною сферою ізоморфна (беручи до уваги властивість инцидентности) планарной моделі, де площину розширена проективної прямої на нескінченності. У цій моделі протилежні точки сфери (щодо центру) вважаються однією точкою.
Щоб зіставити точкам сфери точки на площині, між іншим, що сфера стосується площині в певній точці і цю точку ми виберемо в якості початку координат площині. Тепер проведемо пряму через точку на сфері і центр сфери. Ця пряма перетне сферу в деякій точці. Отриману точку можна використовувати для побудови взаємно однозначного відображення
Прямі на планарной моделі є проекціями великих кіл сфери, оскільки через пряму на площині і початок 3-мірних координат можна провести площину, і ця площина буде перетинати сферу по великому колу.
Як можна бачити, будь великому колу на сфері можна порівняти проектну точку, відповідну єдиною прямою, перпендикулярної площині, на якій окружність лежить і яку можна визначити як двоїсту. Ця пряма перетинає дотичну площину, і це показує, яким чином зіставити єдину точку площині будь-якої прямої цієї площини, таким чином, що точка буде двоїстою до прямої.