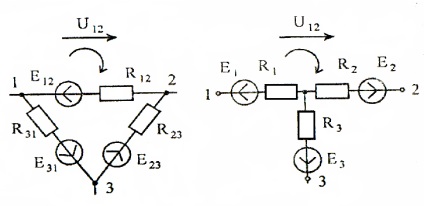
При перетворенні трикутник - зірка в гілках еквівалентної зірки містяться як пасивні елементи (опору), так і активні (джерела ЕРС). Величини еквівалентних ЕРС визначають з умови рівності різниці потенціалів між відповідними вузлами до і після перетворення при повному відключенні перетворюється ділянки від іншої частини ланцюга (малюнок 15). В цьому випадку у всіх гілках трикутника тече струм, а в гілках зірки струми відсутні.
Запишемо другий закон Кірхгофа для гілки R12. E12 трикутника:
Оскільки величини напруг U12 в обох схемах повинні бути однаковими, отримаємо
Аналогічно для інших гілок маємо
Вирази (11) - (14) дають можливість визначати величини еквівалентних ЕРС.
При переході від трикутника до еквівалентної зірці з метою спрощення розв'язуваної задачі величина ЕРС в одній з гілок зірки може бути обрана довільно. Нехай, наприклад, Е3 = 0, тоді з виразів (13), (14) отримаємо:
При переході від зірки кеквівалентному трикутнику як додаткова умова можна прийняти
Тоді і з виразів (12) - (14) отримаємо
Величини еквівалентних опорів зірки і трикутника визначаються за формулами (1) - (6). Розглянемо, наприклад схему Малюнок 16, яка за допомогою перетворення зірки з гілками (R1. Е1), (R2. E2), (R3. Е3) в еквівалентний трикутник отримує вид малюнок 17.
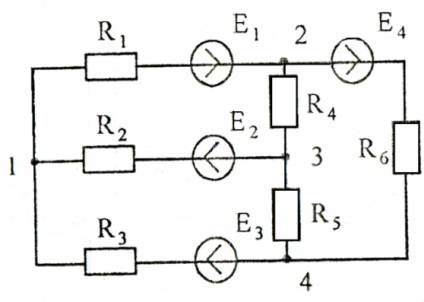
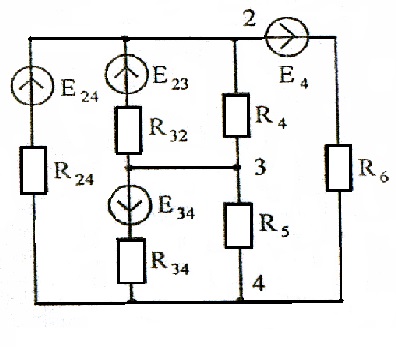
Виберемо в якості додаткової умови
Розглянемо перетворення трикутника 1 2 3 (рисунок 16) в еквівалентну зірку, для чого виділимо його з ланцюга (малюнок 18а).
Напруження між вузлами трикутника і зірки:
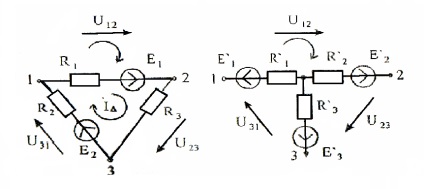
Приймаємо для спрощення. тоді:
У підсумку схема (рисунок 16) приймає вид, представлений на малюнку 19.
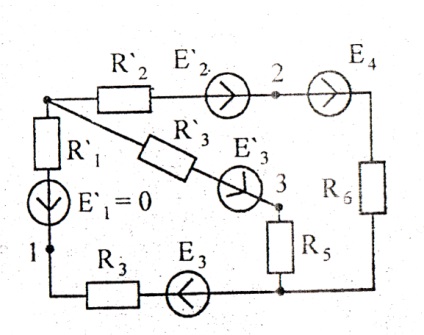
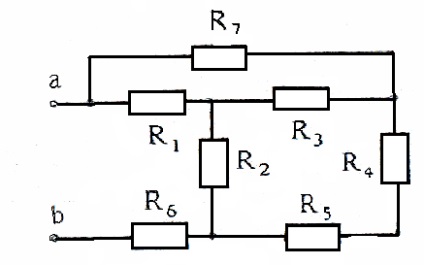
Визначити еквівалентний опір RЕ (рисунок 20, 21, 22) щодо зазначених затискачів, якщо опору рівні 10 Ом. Дані взяти з табл. 1-3 (номер варіанта відповідає порядковому номеру студента в журналі, номеру 11 відповідає 1 варіант).
Завдання №2. Ланцюги однофазного синусоїдального струму
Завданням розрахунку електричного кола є визначення струмів в її гілках, напруг на ділянках ланцюга або потенціалів вузлів. При цьому задаються: конфігурація ланцюга, параметри її елементів і ЕРС, джерел. Для розрахунку струмів в складних електричних ланцюгах застосовуються методи рівнянь Кірхгофа, контурних струмів, вузлових потенціалів, еквівалентного генератора.
Метод рівнянь Кірхгофа
Розрахунок лінійних електричних ланцюгів методом законів Кірхгофа зводиться до вирішення систем алгебраїчних рівнянь щодо невідомих струмів. Так як число невідомих струмів в заданій схемі дорівнює числу гілок n цієї схеми, то система алгебраїчних рівнянь повинна мати n-й порядок.
Нехай k - число вузлів схеми. З принципу безперервності струмів слід, що число лінійно незалежних рівнянь, які можна скласти за першим законом Кірхгофа, так само (k-1) .Недостающіе рівняння, число яких [n- (k-1)], складаються за другим законом Кірхгофа для незалежних контурів , не утримуючи-чих джерел струму. Контури є незалежними, якщо в кожен з них вхо-дит гілка, яка не входить в усі інші.
Розглянемо на прикладі розрахунок струмів в схемі (рисунок 24), яка містить 6 гілок, 4 вузли і 3 незалежних контури. Виберемо довільно напрям струмів в гілках і напрямок обходу незалежних контурів. Перші три рівняння (4 - 1 = 3) запишемо за першим законом Кірхгофа, а решту три (6 - 3 = 3) - по другому законі Кирхгофа:
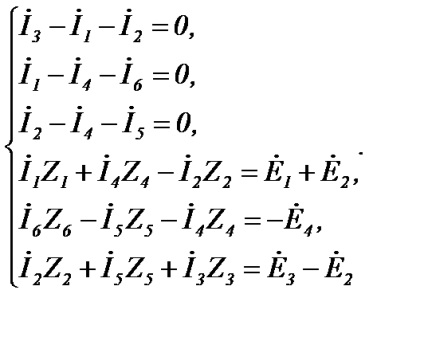
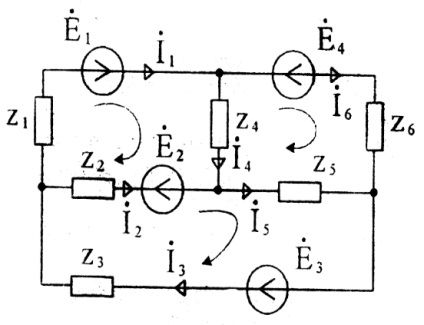
Рішення отриманої системи рівнянь дає шукані струми. Якщо ланцюг містить m гілок з джерелами струму, то число невідомих струмів зменшується до (n-m). За першим законом Кірхгофа число рівнянь залишається без змін (k-1), а за другим законом Кірхгофа вона відповідно зменшується на число гілок з джерелами струму [n- (k-1) -m].
Так, для схеми Малюнок 25, що містить 6 гілок і одне джерело струму, необхідно скласти три рівняння за першим законом Кірхгофа і два - по другому.
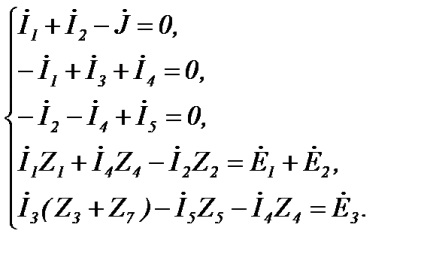
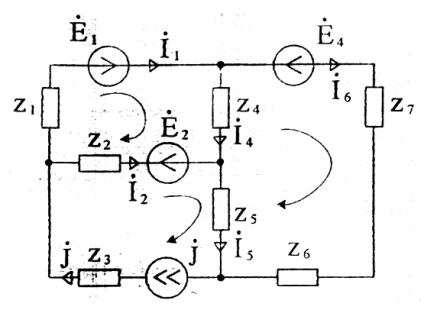
Якщо в результаті розрахунків будь-якої струм вийшов негативним, це означає, що його дійсне напрям протилежний обраному.
До недоліку розглянутого методу слід віднести високий порядок системи рівнянь для розрахунку складних електричних ланцюгів.
Метод контурних струмів
Розрахунок розгалуженої ланцюга може бути зведений до вирішення всього [n- (k-1)] рівнянь, складених за другим законом Кірхгофа. Для цього ланцюг розглядається як сукупність незалежних дотичних контурів і проводиться умовна заміна невідомих струмів в гілках на струми, що протікають по замкнутим контурам. У рівняння, складені за другим законом Кірхгофа, вводяться струми в незалежних контурах - контурні струми.
Дійсні струми в гілках, що належать тільки одному контуру, дорівнюють відповідним контурним струмів (але можуть відрізнятися від них за направленням). Токи в загальних для двох або декількох контурів гілках визначаються як алгебраїчна сума відповідних контурних струмів. Перший закон Кірхгофа при цьому буде виконуватися автоматично. Напрямок контурних струмів вибирається довільно, а обхід контурів усло-вімся проводити в напрямку контурних струмів.
Для ланцюга з джерелами ЕРС система рівнянь, складених для незалежних контурів за другим законом Кірхгофа, містить рівняння типу
де - контурні струми;
- сума опорів гілок, що утворюють незалежний m-й контур (контурне опір),;
- сума ЕРС цього контуру;
Zmq - опір гілки, загальною для m-го і q-контуру (опір зв'язку).
Якщо в загальних (суміжних) гілках напрямки контурних струмів збігаються, то опір зв'язку береться позитивним, якщо струми спрямовані зустрічно, то - негативним. Контурні опору завжди приймаються позитивними.
При записи правій частині рівнянь ЕРС, напрямки яких збігаються з прийнятим напрямом контурного струму (обходу), приймаються позитивними, а при спрямованих протилежно - негативними.
Запишемо систему рівнянь за методом контурних струмів для схеми Малюнок 26:
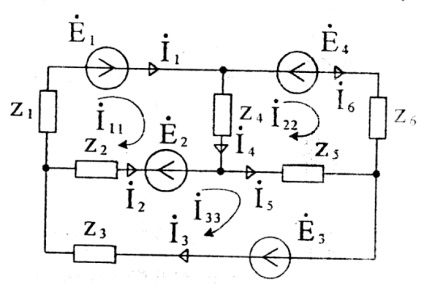
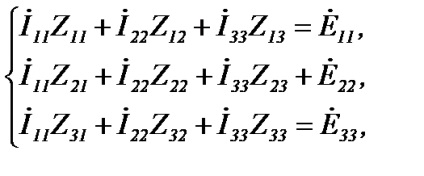
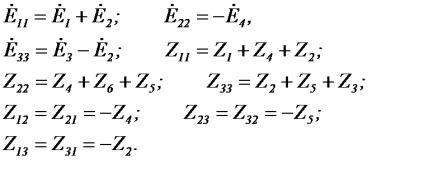
Після рішення системи рівнянь щодо контурних струмів знаходимо струми в гілках:
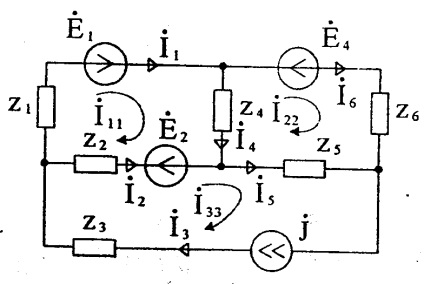
При наявності гілки з джерелом струму вибирається додатковий контур, що включає цей ланцюг. Рівняння для додаткового контуру не складається, тому що контурний струм дорівнює струму джерела. Падіння напруги на опорах зв'язку з іншими від джерела струму (контурного струму) враховуються. Так, для ланцюга (малюнок 27) система рівнянь має вигляд
Метод вузлових потенціалів
Якщо у розгалуженій електричного кола число узловбез одиниці менше, ніж число незалежних контурів (k-1)<[n-(k-1)], удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы алгебраических уравнений (k-1)-го порядка относительно неизвестных потенциалов (узловых потенциалов). При этом потенциал одного из узлов схемы полагают равным нулю.
Рівняння з вузловими потенціалами випливають з першого закону Кірхгофа. Після знаходження невідомих потенціалів визначають струми в гілках за законом Ома.
Рівняння, що входять в систему, є однотипними і для m-го вузла мають такий вигляд:
де - сума провідностей всіх гілок, що сходяться в m-му вузлі,;
- провідність гілки, що з'єднує вузол m c вузлом q. Якщо між будь-якими вузлами немає гілки, то відповідна провідність дорівнює нулю;
- ЕРС джерел, розташованих в галузі між вузлами m або q.
При цьому ЕРС, спрямовані до вузла m (щодо якого складається рівняння), беруться позитивними, а спрямовані від цього вузла - отрица-них.
Складемо систему рівнянь для схеми Малюнок 28, вважаючи:
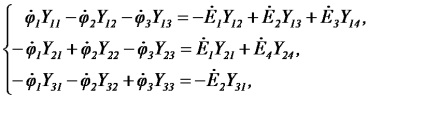
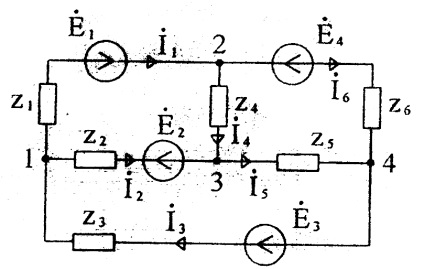
Після визначення потенціалів знаходимо струми згідно із законом Ома:
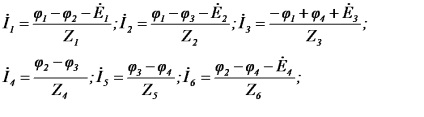
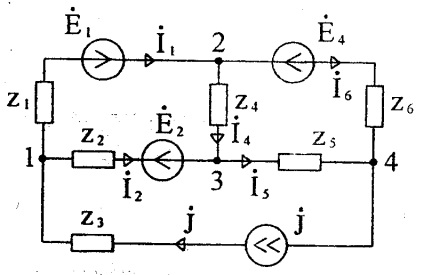
Якщо гілка містить джерело струму, то її провідність дорівнює нулю, тому що внутрішній опір джерела струму дорівнює нескінченності. Якщо до m-му вузлу підтікає струм від джерела струму, то він повинен бути включений в праву частину рівняння зі знаком «плюс», якщо витікає, то зі знаком «мінус». Так, для ланцюга (малюнок 29) система рівнянь має вигляд при:
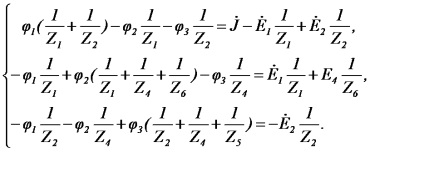
У будь-який електричного кола за законом збереження енергії кількість Вира-бативает за одиницю часу енергії джерел повинна дорівнювати потужності споживачів:
Будь-яке порушення цих співвідношень вказує на неточність проведених обчислень.
Активну і реактивну потужності джерел можна знайти як дійсну і уявну частини повної комплексної потужності джерел:
де - пов'язаний комплекс струму
Якщо напрямок струму збігається з напрямком джерела ЕРС, то произве-дення входить в ліву частину рівності зі знаком «плюс», в іншому випадку - зі знаком «мінус».
Якщо електричне коло містить джерело струму j, то
де - напруга на затискачах джерела струму.
Активна потужність споживачів:
де Iq - діюче значення струму q-й гілки, що містить активний опір Rq.
Реактивна потужність споживачів:
Для індуктивності твір I 2 XL входить в суму зі знаком «плюс», для ємності I 2 Xc - зі знаком «мінус».