Нехай, нарешті, з точки P проведені до еліпсу дві взаємно перпендикулярні дотичні t1 і t2 (див. Рис. 17).

Відобразимо фокус щодо прямої t2 і отриману точку з'єднати з F. Очевидно, що і кут - прямий (останнє випливає з того, що кут між t1 і t2 прямий, і другий теореми Понселе); отже. але; тому. З іншого боку, PO - медіана трикутника, так що. З огляду на попереднє рівність отримуємо: PO 2 = 2a 2 - c 2 або PO 2 = (a 2 - c 2) + a 2 = a 2 + b 2. т. Е. Вершини прямих кутів, сторони яких стосуються еліпса, розташовані на окружності радіуса з центром в центрі еліпса.
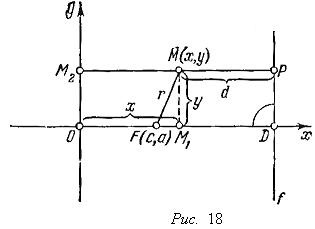
Еліпс як результат стиснення окружності. Нехай точка M. належить еліпсу, віддалена від головної осі x на відстань MM1 = y. а від головної осі y - на відстань MM2 = x (див. Рис. 18). Симетрія еліпса дозволяє обмежитися розглядом точок еліпса, розташованих усередині одного з прямих кутів, утворених головними осями x та y. Зі співвідношень (2) слід:
Після виключення r і d. отримаємо:
звідки, множачи обидві частини рівності на a і враховуючи співвідношення (2). знайдемо остаточно:
Еліпс як результат стиснення окружності.