Вступні випробування з фізики
III. електродинаміка
1 Два маленьких кульки, один з яких спочатку покоївся, а другий мав деяку швидкість, перебуваючи від першого кульки на дуже великій відстані, зблизилися до відстані L. Знаючи, що напрямок швидкості другого кульки залишалося незмінним, знайти величину швидкості v. Впливом на кульки всіх інших тіл і втратами енергії кульок на випромінювання знехтувати. Маса першого кульки дорівнює m, другого - М. Заряд кожного кульки дорівнює q.
За умовою завдання, на кульки не діють інші тіла. Тому можна вважати, що первісний стан системи, що складається з кульок, задано щодо инерциального спостерігача і ця система є ізольованою. Оскільки напрям швидкості другого кульки залишається незмінним, потрібно вважати, що обидві кульки при зближенні рухаються вздовж однієї прямої, і в момент найбільшого зближення відносна швидкість кульок звертається в нуль, тобто швидкості кульок в цей момент щодо зазначеного спостерігача стають рівними:
Оскільки кульки утворюють ізольовану систему, в якій не діють дисипативні сили, то в будь-який момент часу, в тому числі і в момент найбільшого зближення кульок, повинні виконуватися закон збереження імпульсу і закон збереження енергії:
де - електрична стала. При записи закону збереження енергії було враховано, що кульки рухаються поступально, а втратами механічної енергії, зумовленими випромінюванням рухомих з прискоренням заряджених тіл, за умовою задачі, слід знехтувати.
Вирішуючи спільно наведені рівняння, знаходимо шукану величину швидкості:
2 На тонкий гладкий горизонтальний діелектричний стрижень надіті дві маленькі намистинки зарядами + q і -q, скріплені між собою діелектричної пружиною жорсткістю k. Вся система знаходиться в однорідному електричному полі, силові лінії якого паралельні стрижня. При цьому пружина не деформована. Якщо змінити напрямок поля на протилежне, залишивши незмінною величину його напруженості Е, то довжина пружини при рівновазі зменшиться в n = 2 рази. Нехтуючи поляризацією діелектриків, знайти величину Е.
Будемо вважати, що стрижень з кульками і джерело зовнішнього електричного поля покояться щодо деякої інерціальної системи відліку. Тоді, нехтуючи відповідно до умовою завдання силами тертя між кульками і стрижнем і поляризацією пружини і стрижня, можна стверджувати, що сили, які діяли на кульки з боку електричного поля при первісної орієнтації вектора напруженості цього поля, врівноважували сили взаємного тяжіння кульок, тобто . мало місце співвідношення
де l0 - довжина недеформованою пружини, - електрична постійна.
Після зміни напрямку вектора напруженості зовнішнього поля в кінцевому стані рівноваги довжина пружини, за умовою задачі, стає в n разів менше первісної. Отже, відповідно до законів Кулона і Гука має виконуватися співвідношення
Підставляючи в це вираження значення qE з попереднього рівняння, знаходимо, що довжина пружини в недеформованому стані повинна задовольняти співвідношенню а шукана величина напруженості поля дорівнює
3 На відстані 2R від центру закріпленого проводить кулі радіусом R утримують позитивний точковий заряд 2Q. Заряд кулі дорівнює Q. Яку швидкість v може придбати електрон, початківець свій рух з нескінченно віддаленої точки, до моменту потрапляння на кулю?
При вирішенні задачі будемо припускати, що куля покоїться щодо деякої інерціальної системи відліку, електрон рухається у вакуумі і можна знехтувати втратами енергії електрона на випромінювання, тобто вважатимемо, що прискорення електрона досить мало. При наближенні електрона до кулі в силу явища електростатичної індукції має відбуватися перерозподіл зарядів кулі. Будемо вважати, що матеріал кулі має досить великий провідність, а тому можна знехтувати втратами енергії, викликаними виділенням джоулева тепла при протіканні струмів провідності, і вважати, що всі крапки проводить кулі мають однаковий потенціал, а тому весь його надмірне зарядження, як і в електростатики , розподілений тільки по поверхні кулі.
Нехай величина заряду, що знаходиться на досить малому i-м шматочку поверхні кулі, дорівнює qi. За умовою завдання, куля ізольований, a його заряд дорівнює Q. Тому, відповідно до закону збереження заряду і зробленим вище припущенням, в будь-який момент часу за всіма шматочках поверхні кулі дорівнює Q.
Будемо, як звичайно, вважати, що потенціал електростатичного поля, створюваного спочиваючим точковим зарядом q у нескінченно віддаленій від нього точці, дорівнює нулю. Тоді потенціал електростатичного поля на відстані r від точкового заряду, як відомо, буде дорівнює
де - електрична стала. Згідно з принципом суперпозиції потенціал, що створюється системою точкових зарядів в даній точці, дорівнює сумі потенціалів, створюваних кожним з цих зарядів порізно в цій точці. Отже, потенціал центру кулі щодо нескінченно віддаленої від нього точки, зумовлена надмірним зарядом кулі і точковим зарядом 2Q, що знаходиться від центру кулі на відстані 2R, дорівнює
Відповідно до сказаного вище, таким же повинен бути потенціал і будь-якої точки поверхні кулі, причому з отриманого виразу випливає, що цей потенціал не залежить від положення електрона. Тому при виконанні зроблених вище припущень робота сил електростатичного поля, що породжується зарядами кулі і зарядом 2Q, над переміщається в цьому полі електроном не залежить від виду траєкторії електрона, а визначається лише його початковим і кінцевим положеннями. Оскільки заряд електрона негативний, вказане поле в ході руху електрона до кулі зробить над електроном позитивну роботу де - модуль заряду електрона. Звідси, відповідно до закону зміни кінетичної енергії, слід, що шукана величина швидкості електрона масою m при його попаданні на поверхню кулі з урахуванням втрат енергії електрона на випромінювання і джоулево тепло в кулі повинна задовольняти нерівності
4 В схемі, показаної на рис. 1, через резистор R1 = 15 Ом тече струм I = 10 А, величина якого не залежить від положення движка реостата R. Знайти величини ЕРС батарей в цій схемі, якщо внутрішній опір першої батареї r1 = 5 Ом.
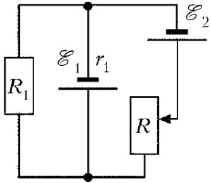
При вирішенні задачі будемо, як завжди, нехтувати опором проводів і контактів між елементами схеми. Оскільки резистор R1. перша батарея і друга батарея разом з реостатом R з'єднані паралельно, падіння напруги на резисторі R1 на першій батареї і на другий батареї з реостатом R повинні бути однаковими. Нехай сума внутрішнього опору другої батареї і включеної в схему частини реостата R дорівнює r2. Тоді, відповідно до сказаного і закону Ома, повинні виконуватися співвідношення:
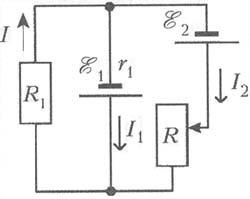
При написанні цих співвідношень передбачалося, що напрямки струмів в гілках схеми відповідають стрільцям, показаним на рис. 2. В силу закону збереження заряду і сталості струмів в гілках схеми при зазначених напрямках струмів їх величини повинні задовольняти співвідношенню I = I1 + I2. а тому сила струму через резистор R1 повинна задовольняти рівнянню
Це рівняння буде тотожністю при будь-яких r2. якщо = IR1 (тобто I2 = 0) і = I (R1 + r1). Таким чином, шукані величини ЕРС рівні:
5 По двох паралельних шин, закріпленим під кутом = 45 ° до горизонту, може ковзати, залишаючись перпендикулярної їм, перемичка. Шини з'єднані між собою нерухомим провідником. Опір перемички багато більше опору шин і провідника. Вся система знаходиться в однорідному магнітному полі, індукція якого B перпендикулярна площині шин. Якщо напрямок магнітного поля зробити вертикальним, не змінюючи величини B, то стала швидкість перемички буде відрізнятися в k = 0,8 рази від раніше спостерігалася. Нехтуючи индуктивностью проводить контуру, знайти коефіцієнт тертя перемички про шини.
При вирішенні задачі будемо вважати, що шини і з'єднує їх провідник нерухомі разом з джерелом магнітного поля щодо лабораторної системи відліку і ця система є інерціальній. При русі перемички буде змінюватися потік магнітного поля, зчеплений з проводять контуром, утвореним перемичкою, шинами і з'єднує їх провідником. Тому в цьому контурі повинен виникнути індукційний струм, напрямок якого, згідно з правилом Ленца, повинне бути таким, щоб рух перемички гальмувалося. Гальмувати рух перемички будуть і сили тертя, що діють на перемичку з боку шин. Отже, перемичка в сталому режимі може ковзати по шинам тільки вниз. З урахуванням сказаного, на рис. 3 показані сили, що діють на ковзаючу вниз по шинам перемичку, коли вектор індукції В зовнішнього магнітного поля спрямований перпендикулярно шинам. Тут mg - сила тяжіння, m - маса перемички, g - прискорення вільного падіння. Сила реакції шин показана на малюнку у вигляді двох складових: нормальної N і тангенціальною Fтр, званої зазвичай силою сухого тертя ковзання, величина якої, відповідно до закону Кулона-Амонтона, дорівнює N. Нарешті, FA - сила Ампера. Відповідно до закону Ампера, ця сила спрямована перпендикулярно вектору В індукції магнітного поля і перемичці, тобто паралельно шинам, причому з двох можливих напрямків вибрано те, яке, як було зазначено вище, узгоджується з правилом Ленца. Зі сказаного і другого закону Ньютона випливає, що рівняння руху перемички в проекції на вісь, направлену паралельно шинам вниз, має вигляд
де а - проекція прискорення перемички на зазначений напрямок.
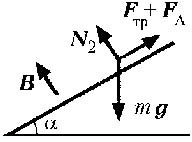
Оскільки перемичка рухається по шинам, то величина нормальної складової сили реакції шин N = mg cos. Якщо відстань між шинами позначити L, а опір перемички R, то, згідно з правилом потоку Фарадея-Максвелла і закону Ома, сила струму, поточного по перемичці при величині швидкості її руху, що дорівнює 1. повинна бути дорівнює I1 = BL1 / R, т. к. за умовою завдання, опором інших елементів проводить контуру і його индуктивностью слід нехтувати. З огляду на, що індукція магнітного поля і перемичка взаємно перпендикулярні, знаходимо величину сили Ампера: а потім з рівняння руху отримуємо, що при сталому русі перемички (тобто при a = 0) величина її швидкості
У разі, коли зовнішнє магнітне поле направлено вертикально, що діє на перемичку силу Ампера, спрямовану горизонтально, зручно представити у вигляді двох компонент, одна з яких спрямована паралельно шинам, а інша - перпендикулярно до них, як показано на рис. 4. Повторюючи практично дослівно наведені вище міркування, можна довести, що при швидкості руху перемички, що дорівнює 2, через перемичку повинен протікати струм При цьому зазначені компоненти сили Ампера дорівнюватимуть
і а рівняння руху перемички в проекції на спрямовану вниз паралельно шинам вісь матиме вигляд де
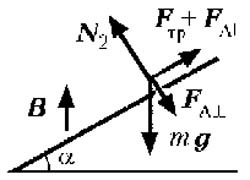
Отже, в цьому випадку величина швидкості усталеного руху перемички при виконанні зроблених припущень дорівнює
Якщо, як зазвичай, вважати, що коефіцієнт тертя не перевищує одиниці, то з отриманих виразів випливає, що а тому, згідно з умовою завдання, і шуканий коефіцієнт тертя
Якщо ж вважати, що коефіцієнт тертя перевищує одиницю, що зазвичай не має місця, то, і шукана величина повинна дорівнювати
Продовження в № 18