Глава V. Метод координат в просторі. § 1. Координати точки і координати вектора. → номер 406
Розглянемо загальний випадок. Розглянемо два некомпланарних вектора AB і DC. Перенесемо вектор DC паралельно так, щоб точка D1 його початку збіглася з точкою В кінця першого вектора. Отримаємо вектор D1C1 або, що те ж саме, вектор ВС1 сонаправленнимі з вектором DC і рівний йому по довжині. Згідно з правилом додавання векторів:
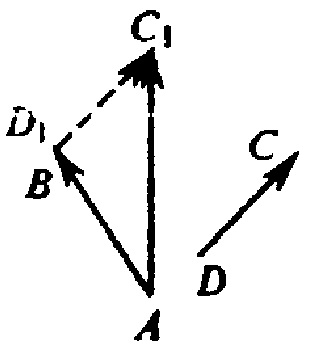
Для доказу висловимо координати цих векторів через координати
Їх початку і кінця.
З позначення координат вектора AB як х1, у1 і z1 і вектора BC1 як x2, у2, z2, отримаємо
Суми координат x1 + x2, y1 + y2, z1 + z2 є координатами вектора АС1 рівного сумі вихідних двох векторів AB і DC. Що й потрібно було довести.
← 407. Дано вектори а, b, с і d<— 2,7; 3,1; 0,5>. Знайдіть координати векторів: а) а + b; б) а + с; в) b + с; г) d + b; д) d + a; е) а + b + с; ж) b + а + d; з) а + b + c + d