Форма параболи. Рівняння параболи. Парабола однозначно визначається своїм фокусом F і директоркою f. Перпендикуляр x ≡ FD. опущений з фокуса на директрису, називають віссю параболи, а відстань p від фокуса до директриси - її параметром (див. Рис. 1).
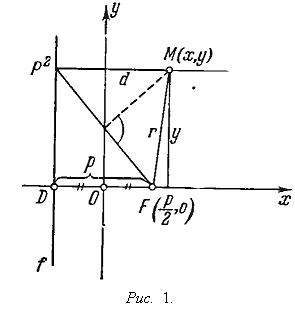
З визначення параболи як геометричного місця точок, рівновіддалених від F і f. випливає, що парабола симетрична щодо своєї осі. причому вісь x має з параболою лише одну спільну точку O - середину відрізка FD. Точка O називається вершиною параболи.
Проведемо через точку O пряму y. перпендикулярну до осі x. Очевидно, що крім точки O на прямий y інших точок параболи немає, т. К. Для будь-якої точки P прямий y. відмінною від O. відстань r до фокусу більше, відстань PP1 = d до директриси одно і, отже, r. d> 1, т. е. точка P не належить параболі. Для будь-якої точки P площині, розташованої з фокусом F по різні боки від директриси, r> d. і тому в цій напівплощини точок параболи немає. Отже, точки параболи розташовані по ту сторону від прямої y. з якої розташований фокус параболи. В силу симетрії всяка пряма, паралельна прямій y і має з параболою одну спільну точку, має з нею і іншу загальну точку і лише пряма y має одну спільну точку з параболою. Внаслідок цього пряму y називають дотичній до параболи в її вершині.
Приймемо тепер вісь параболи x за вісь абсцис, а дотичну y в вершині - за вісь ординат прямокутної системи координат. Нехай M (x. Y) - довільна точка параболи (див. Рис. 1). тоді
і з рівності r 2 = d 2 слід, що
Форма параболи, рівняння параболи, вісь і параметр параболи, дотична до параболи і її вершині.