Будемо шукати рішення наведеного хвильового рівняння. описує поширення такого пучка у вигляді [1]
де u (x, y, z) - повільно змінюється комплексна функція, яка і визначає властивості лазерного пучка, що відрізняють його від плоскої хвилі. Застосовуючи оператор Δ до функції Ψ, маємо
Якщо у виразі знехтувати другої похідної u по z в порівнянні c першої, то на підставі наведеного хвильового рівняння Гельмгольца отримаємо рівняння
Отримане рівняння відноситься до рівнянь параболічного типу, а саме наближення, в рамках якого воно було отримано, називається параболічним наближенням. Неважко показати, що рівняння буде задовольняти гаусів пучок, амплітуда якого змінюється по поперечної координаті по гауссова закону.
Для гауссова пучка можна записати вираз
де r 2 = x 2 + y 2. Параметр р - комплексний фазовий зсув при поширенні світла вздовж осі z, а q - комплексний параметр пучка, що визначає гауссово розподіл поля по координаті r, де r - відстань від осі. Крім того, q визначає кривизну хвильового фронту, який поблизу осі є сферичним.
Розглянемо властивості гауссова пучка з довжиною хвилі λ більш докладно. Для цього висловимо комплексний параметр q через два дійсних параметра пучка R і w
де R є радіус кривизни хвильового фронту, а w характеризує зміну поля Е в поперечній площині (параметр w прийнято називати шириною пучка). Розподіл поля в цій площині, підкоряється закону Гаусса, і w дорівнює відстані, на якому амплітуда поля убуває в е разів у порівнянні з полем на осі.
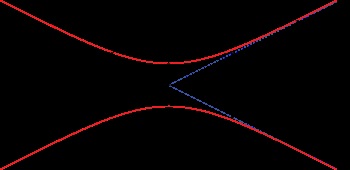
Ширина гауссова пучка w (z) як функція z. w0. горловина пучка; b. глибина різкості; zR. довжина Релея; Θ: кутова розбіжність пучка
Ширина пучка
В деякій площині, званої горловиною каустичної поверхні або перетяжкой, гаусів пучок стягується до мінімальної ширини w0. У цій площині, від якої доцільно відраховувати відстань z, фазовий фронт є плоским, і комплексний параметр пучка стає чисто уявним
де zR - довжина Релея. Тоді ширина пучка на відстані z задається наступною формулою
радіус кривизни
Залежність радіусу кривизни від координати
розбіжність пучка
Утворює пучка w (z) є гіперболу, асимптота якої нахилена до осі під кутом
Цей кут дорівнює куту дифракції основної моди в дальній зоні.
Загальна кутова розбіжність пучка складе
Моди вищих порядків

Перші дев'ять Ерміттово-гауссова мод
Гаусові пучки - лише одне з можливих рішень параксіального хвильового рівняння. Комбінації різних ортогональних рішень використовуються для моделювання лазерних пучків. У загальному випадку, якщо визначений повний базис рішень, то будь-який пучок може бути описаний як суперпозиція рішень з базису.