Зрушенням називається такий вид деформації, при якій в будь-якому поперечному перерізі бруса виникає тільки поперечного-ва сила. Деформацію зсуву можна спостерігати, наприклад, при різанні ножицями металевих смуг або прутків (рис. 20.1, а).
Розглянемо брус площею поперечного перерізу А, перпен-дікулярно осі якого прикладено дві рівні і протипожежні-помилково направлені сили F; лінії дії їх паралельні і
знаходяться на відносно не-великій відстані один від одного. Для визначення попе-річковий сили Q застосуємо ме-тод перетинів (рис, 20.1, б).
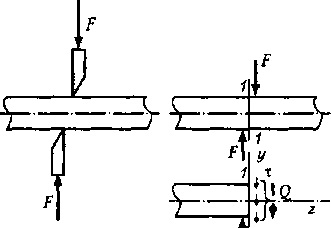
У всіх точках поперечного перерізу діють распреде-лені сили, рівнодіюча-щую яких визначимо з ус-ловия рівноваги залишеної частини бруса;
звідки визначимо поперечну силу
Поперечна сила є рівнодіюча внутрішніх касатель-них сил в поперечному перерізі при зсуві.
Природно вважати, що при зсуві в поперечному перерізі бруса діють тільки дотичні напруження т. Припускаючи третьому, що ці напруги розподілені по перерізу рівномірно і, отже, їх можна визначити за формулою
Очевидно, що при зсуві форма перетину на значення напруги-ня не впливає.
Примітка. Викладений в цьому підрозділі розрахунок дотичних напружень при зсуві наближений, так як лінії дії сил FіQ (див. Рис. 20.1, б) не спрямовані по одній прямій і, строго кажучи, ці сі-ли не є врівноваженою системою, а являють собою пару сил . Однак момент цієї пари (з огляду на малий плеча) невеликий, і відпо-інди їй напруженнями можна знехтувати.
Розрахунки на міцність при зсуві
Умова міцності деталі конструкції полягає в тому, що найбільшу напругу, що виникає в ній (робоча напруга), не повинно перевищувати допустиме.
Розрахункова формула при зсуві
читається так: дотичне напруження при зсуві, обчислене за формулою% = Q / А, не повинно перевищувати допускається-моє.
З цієї розрахунковій формулі проводять проектний і провероч-ний розрахунки і визначають допустиме навантаження.
Деформація зсуву, доведена до руйнування матеріалу, на-ни опиняються зрізом (стосовно металевих деталей) або сколюванням (стосовно до неметалічних конст-рукцій).
Напруга, що допускається на зріз вибирають для пластичних ма-ріалів в залежності від межі текучості. У машинобудуванні для штифтів, болтів, шпонок і т.п. приймають
Для деревини допустимі напруження на сколювання у вруб-ках коливаються в межах від 0,5 до 1,4 МПа і залежать від сорту дере-ва і напрямки врубки по відношенню до напрямку волокон.
При розрахунках на зріз в разі, якщо з'єднання здійснюється декількома однаковими деталями (болтами, заклепками і т.д), вважають, що всі вони навантажені однаково.
Розрахунки з'єднань на зріз зазвичай супроводжують перевіркою міцності етіх'еедіненій на зминання.
Приклад 20.1. Визначити силу F, необхідну для пробивання квад-ратної отвори розміром а = 25 мм в сталевій смузі товщиною 5 = = 10 мм, якщо межа міцності при зрізі тв - 360 МПа. Визначити на-напруги стиснення в пуансоні (рис. 20.2).
Рішення. Визначимо руйнівне навантаження F:
Площа зрізу АСР дорівнює площі бічної поверхні пробитого від-верстия:
Др = = 4 * 25 * КГ 3 • 10 • Ю '3 = 1000 10 "* м 2. Отже, F - тв д.р = 360-10 6 -1000 10 -6 = 360 10 3 Н.
Визначимо напруги стиснення в пуансоні:
де А - площа поперечного перерізу пуансона;
Л = л 2 = 25 2 -10- 6 = 625-10- 6 м 2,
<ус = F/A= 360-10 3 / (625 ■ 10 -6 ) = 576 1 0 6 Па = 576 МПа.
Приклад 20.2. Визначити напруги зминання і зрізу в голівці стрижня, розтягуємо силою F = 100 кН. Дано: D = 32 мм, d = 20 мм, h = = 12 мм (рис. 20.3).
Рішення. Визначимо площа зминання ЛСЧ1 і площа зрізу АСР го-спритні. Площа опорної поверхні головки, що працює на зминання, дорівнює
Площа зрізу дорівнює площі бічної поверхні циліндра діа-метром d і висотою h \
Визначимо напруги зминання і зрізу головки:
Приклад 20.3. В умовах прикладу 19.6 визначити напруги зрізу в болті (див. Рис. 19.14).
Рішення. Напруження зрізу в болті визначаємо за формулою т = F / Др. Площа зрізу ЛСР є дві площі поперечного-ного перетину болта:
АСР = 2nd 2/4 = nd 2/2,
Деформація і закон Гука при зсуві
Для встановлення параметрів, що характеризують деформацію при зсуві, розглянемо елемент бруса у вигляді паралелепіпеда abed, на межі якого дію-вують тільки дотичні напруження х, а протипожежні-неправдиву грань паралелепіпеда представимо жорстко за-щемленной (рис. 20.4). Деформація зсуву в зазначений-ном елементі полягає в перекошування прямих кутів паралелепіпеда за рахунок поступального пере-ня межі ЬС по відношенню до перетину, прийнято * му за нерухоме. Деформація зсуву характеризують-ся кутом у і називається кутом зсуву, або про т - Ріс.20.4 відносна зрушенням (так як цей параметр
не залежить від відстані h, на якому відбувається зсув). Величи-на bbv на яку зміщується рухлива грань відносно не-рухомий, називається абсолютним зрушенням. Відносна-ний зсув у виражається в радіанах.
Напруги і деформації при зсуві пов'язані між собою за-Вісім, яка називається законом Гука при зсуві.
Закон Гука при зсуві справедливий лише в певних преде-лах навантаження і формулюється так: дотичне напруження прямо пропорційно відносного зсуву.
Математично закон Гука можна записати у вигляді рівності
Коефіцієнт пропорційності G характеризує жест-кість матеріалу (тобто здатність чинити опір пружним де-формацій) при зсуві і називається модулем зсуву або модулем пружності другого роду.
Модуль пружності і напруга виражаються в однакових одиницях:
Наведемо значення G, МПа, для деяких матеріалів:
Латунь (3,5. 3,7) -10 4
Алюміній (2,6. 2,7V 10 4
На закінчення відзначимо, що між трьома пружними постійні-ми Е, G і v існує наступна залежність:
Беручи для сталей v = 0,25, отримуємо
Закон парності дотичних напружень
Закон парності дотичних напружень фор-муліруется так: дотичні напруження в двох взаємно-перпен- дікулярних майданчиках, перпендикулярні їх загальному ребру, рівні по модулю.
Усередині тіла поблизу деякої точки виріжемо елементарний паралелепіпед з розмірами dr, dу, dz (рис. 20.5, а).
Нехай на верхній межі цього паралелепіпеда діє каса-тельное напруга т. Сила, що діє в цій межі, дорівнює
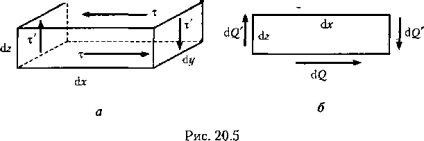
Так як паралелепіпед знаходиться всередині тіла в рівновазі, то - О, отже, на нижній грані паралелепіпеда буде
діяти така ж сила dQ, але спрямована в протилежний-ву сторону. Пара сил (dQ, dQ) буде прагнути обертати парал-лелепіпед проти годинникової стрілки (рис. 20.5, б).
Так як паралелепіпед знаходиться в рівновазі, то = 0,
отже, пара сил (dQ, dQ) буде врівноважуватися ка-кой-то іншою парою з моментом, рівним моменту першої пари. Природно вважати, що друга пара утворюється дотичними на-пряжене т ', що діють на бічних (правої і лівої) гра-нях паралелепіпеда, причому dQ' =% 'dydz. отже,
xdxdydz - t 'dxdydz,
Звернемо увагу на те, що парні дотичні напруження в двох взаємно-перпендикулярних перетинах спрямовані або до лінії перетину площин перетинів, або від цієї лінії.
Напруження в похилих перетинах при розтягуванні.
Через будь-яку точку деформованого тіла можна провести безліч різноорієнтованих січних площин.
Розглянемо прямий брус постійного поперечного перерізу А, розтягується силами F (рис. 20.6, а). Розсічений брус площиною 1-1, що проходить через точку В і складовою з поперечним се-ням кут <р, отбросим верхнюю часть и рассмотрим равновесие нижней.
Очевидно, що рівнодіюча-щая N внутрішніх сил, що діють щих в похилому перерізі, буде дорівнює розтягує силі F:
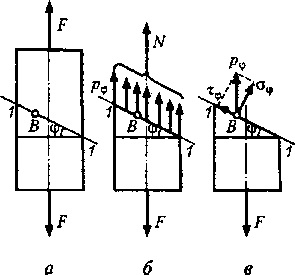
а напруги рф будуть паралель-ни осі бруса (рис. 20.6,6). Вважаючи, що напруги pv розподілені по похилому перерізі рівномірний-но, отримаємо
де ЛФ - площа похилого січі-ня.
Нормальні напруги про в поперечному перерізі дорівнюватимуть
Розкладемо повне напруга р в точці похилого перерізу на нормальне сф і дотичне тф напруги (рис. 20.6, в); тоді
= Рф costp = acos 2 ф;
= Ру sincp = стсоеф ЕТФ - (о / 2.) 5т2ф.
Звідси випливає висновок: при розтягуванні бруса в похилих січі-пах виникають рівномірно розподілені по перетину нормаль-ні та дотичні напруження і відповідні цим напря-жениям деформації розтягу та зсуву.
Розглянемо окремі випадки:
Нормальні напруги мають максимальне значення в по-перцевому перетині:
Дотичні напруження в поперечному перерізі дорівнюють нулю;
Дотичні напруження досягають свого максимального зна-чення в перетинах, нахилених до осі під кутом 45 °. Ці напруги-ня є причиною появи на розтягується зразку при досягненні межі текучості сітки похилих ліній Людер- са-Чернова;
У поздовжніх перетинах бруса немає ні дотичних, ні нормаль-них напруг (згадаємо гіпотезу про ненадавліваніі волокон).
З викладеного випливає, що, кажучи про напругу в даній точці, завжди необхідно вказати положення січної площини, в якій це напруга виникає.
Сукупність нормальних і дотичних напружень, метушні-кающих в незліченній кількості різноорієнтованих майданчиків, що проходять через дану точку, характерізуетнапря-женное стан в даній точці.
Майданчики, в коториекасательние напруги дорівнюють нулю, на-зиваютсяглавнимі майданчиками, а виникають в них нормальні напруги -головний напряженіямі.Как доводиться в теорії пружності, в загальному випадку напруженого стану в зоні досліджуваної точки можуть існувати три вза-імно-перпендикулярні головні майданчики. «
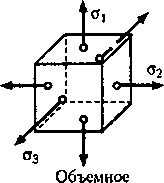
Залежно від числа таких майданчиків (де а * 0) відмінності-ють три основних види напруженого стану: лінійне (одновісне), плоске (двовісний) іоб'емное (тривісне) (рис. 20.7).
Надалі нас будуть цікавити тільки перші два види напруженого стану.
Очевидно, що в розглянутому випадку одноосного розтягу головні майданчики розташовані в поперечному і поздовжньому січі-пах, тобто взаємно-перпендикулярні. Звернемо увагу також на
то, чтоглавние напряженіяв дан-ної точкеімеют максимальне і мінімальне значення '.
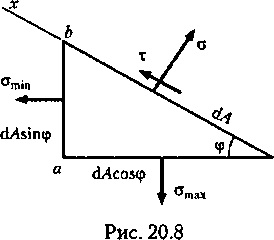
Надалі нам знадобиться-ся залежність між нерівними нулю головними напруженнями в двох взаємно-перпендикулярних майданчиках (випадок плоского на-напруженого стану) і максі
мінімальними дотичними напруженнями в похилій (по ставлення-ня до головних) майданчику.
Розглянемо рівновагу призми, для чого спроеціруем дію-ють на її гранях сили на осьх:
З цього рівняння випливає, що при <р = 45°
Якщо в разі плоского напруженого стану в околі-сти даної точки можна виділити елементарний паралелепіпед таким чином, щоб на його гранях діяли тільки рівні між собою дотичні напруження (див. Рис. 20.5, а), то такий вид напруженого стану називаетсячістим сдвігом.В надалі з чистим зсувом ми зустрінемося при вивченні теорії крутіння круглого циліндра.