В теорії графів глибина дерева зв'язкового неориентированного графа G - це числовий інваріант G. мінімальна висота дерева трьома [en] для суперграфа графа G. Цей інваріант і близькі поняття зустрічаються під різними іменами в літературі, включаючи число ранжирування вершин, впорядковане хроматичної число і мінімальна висота виключення дерева. Поняття близьке також до таких понять, як циклічний ранг [en] орієнтованих графів і висота ітерації мови регулярних мов [1]. Інтуїтивно, якщо деревна ширина графа вимірює, наскільки граф далекий від дерева, глибина дерева вимірює, наскільки граф далекий від зірки.
Глибину дерева графа G можна визначити як мінімальну висоту лісу F з властивістю, що будь-який ребро графа G з'єднує пару вершин, пов'язаних ставленням предок-нащадок в F [2]. Якщо G зв'язний, цей ліс повинен бути єдиним деревом. Ліс не обов'язково повинен бути подграфом графа G. але якщо є, то це дерево трьома [en] для G.
Безліч пар предок-нащадок в F утворює тривіально досконалий граф [en]. і висота F є розміром найбільшою кліки цього графа. Таким чином, глибину дерева можна альтернативно визначити як розмір найбільшою кліки в тривіально скоєному суперграфе графа G. що є дзеркальним відображенням деревної ширини. яка на одиницю менше розміру найбільшої кліки в хордального суперграфе графа G [3]
Інше визначення наступне:
де V - безліч вершин графа G і G i> - зв'язкові компоненти G [4]. Це визначення дзеркально відображає визначення циклічного рангу [en] орієнтованих графів, яке використовує сувору зв'язність і строго пов'язані компоненти замість неориентированной зв'язності і зв'язкових компонент.
Глибину дерева можна визначити з використанням розмальовки графів. Центрована розфарбування графа - це розфарбування вершин, що має властивість, що в будь-якому зв'язковому породжених підграфі є колір, який зустрічається рівно один раз. Тоді глибина дерева - це мінімальний розмір квітів, необхідних для центрованої розмальовки графа. Якщо F - ліс з висотою d. має властивість, що будь-який ребро графа G з'єднує предка і нащадка в дереві, то можна отримати центрированную розмальовку графа Gd квітами шляхом розфарбовування кожної вершини в колір з номером, рівним відстані від кореня в графі F [5].
Нарешті, можна визначити його в термінах фішечной гри [en]. Точніше, в точності як гра «поліцейські-грабіжники» [en]. Уявімо таку гру на неорієнтованому графі. Є два гравці, грабіжник і поліцейський. Грабіжник має одну фішку, яку він рухає вздовж ребер графа. Поліцейський має необмежену кількість фішок, але він хоче мінімізувати кількість використаних фішок. Поліцейський не може пересувати свої фішки, поміщені на граф. Гра відбувається в такий спосіб. Грабіжник розміщує свою фішку, потім поліцейський повідомляє, куди він хоче поставити наступну фішку і грабіжник після цього може пересунути свою фішку уздовж ребер, але не через зайняті вершини. Гра завершується, коли поліцейський поміщає наступну фішку поверх фішки грабіжника. Глибина дерева даного графа визначає мінімальне число фішок, необхідних для гарантованого виграшу [6] [7]. Для зірок досить двох фішок - розміщуємо першу фішку в центрі зірки, змушуючи грабіжника перейти в який-небудь промінь, а потім поміщаємо другу фішку на фішку грабіжника. Для шляху з n вершинами поліцейський використовує стратегію довічного пошуку. яка гарантує використання не більше ⌈ log 2 (n + 1) ⌉ (n + 1) \ rceil> фішок.
Глибина дерева повного графа дорівнює числу його вершин, і в цьому випадку єдиним можливим лісом F. для якого будь-яка пара вершин повинна бути відносно предок-нащадок, є одиночний шлях. Схожим чином глибина дерева повного двудольного графа Kx, y дорівнює min (x, y) + 1, і як би ми не мали вершини, листя лісу F повинні мати щонайменше min (x, y) предків в F. Ліс, на якому досягається min (x, y) + 1, може бути побудований шляхом освіти шляху з вершин меншою за розміром частки графа, а вершини більшої частки формують листя дерева F. з'єднані з нижньою вершиною шляху.
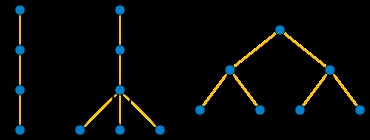
Глибина дерева шляху з n вершинами дорівнює в точності ⌈ log 2 (n + 1) ⌉ (n + 1) \ rceil>. Ліс F. представляє цей шлях з такою глибиною, можна утворити, помістивши корінь в середню точку шляху F і продовжуючи рекурсию в двох менших шляхах по обидва боки від кореня [8].
Глибина дерев і зв'язок з деревної шириною
Будь-ліс з n вершинами має деревну глибину O (log n). Для лісу можна завжди знайти постійне число вершин, видалення яких дає ліс, який можна розділити на два менших Підлісся з максимум 2n / 3 вершин в кожному. Рекурсивно ділячи ці два Підлісся, легко можна досягти логарифмічну верхню межу деревної глибини. Та ж техніка, застосована до декомпозиції дерева [en] графа, показує, що якщо деревна ширина n -вершина графа G дорівнює t. тоді деревна глибина графа G дорівнює O (t log n). [9] Оскільки внешнепланарние графи. паралельно-послідовні графи і графів Халіна мають обмежену ширину дерев, вони все теж мають максимум логарифмічну глибину дерев.
В іншому напрямку ширина дерева графа не перевищує його глибину дерева. Точніше, ширина дерева не перевищує шляхову ширину графа [en]. яка максимум на одиницю менше його глибини дерева [10] [11].
Мінор графа G - це інший граф, утворений з подграфа графа G стягуванням деяких ребер. Глибина дерева монотонна по минорам - будь-який мінор графа G має глибину дерева, яка не перевищує глибину дерева самого графа G [12]. Таким чином, по теоремі Робертсона-Сеймура, для будь-якого фіксованого d безліч графів з глибиною дерева, що не перевищує d. має кінцеве число заборонених миноров.
Якщо C - клас графів, замкнутих щодо освіти миноров, то графи в C мають деревну глибину O (1) тоді і тільки тоді, коли C не покриває всі варіанти шляху [13].
Деревна глибина має тісний зв'язок з теорією породжених подграфов графа. У класі графів, що мають деревну глибину не більше d (для будь-якого фіксованого натурального d), властивість бути породженим подграфом є цілком квазіупорядоченним [en] [14]. Основна ідея докази, що цей зв'язок цілком квазіупорядоченна, полягає в використанні індукції по d. Ліси висоти d можна інтерпретувати як послідовність лісів висоти d - 1 (утворених видаленням коренів дерев висоти d) і можна використовувати лемму Хігмана [en]. щоб показати, що ці послідовності цілком квазіупорядоченни.
З цілком квазіупорядоченності випливає, що будь-яку властивість графа, монотонне по породженим подграфа, має кінцеве число заборонених породжених подграфов, а тому може бути перевірено за поліноміальний час на графах з обмеженою деревної глибиною. Графи з деревної глибиною, що не перевищує d. самі по собі мають кінцеве число заборонених породжених подграфов. [15]
Якщо C є класом графів з обмеженою виродженням [en]. графи в безлічі C мають обмежену деревну ширину тоді і тільки тоді, коли існує шлях, який не може з'явитися в якості породженого подграфа в C [13].
Визначення глибини дерева є складною обчислювальної завданням - відповідне завдання розпізнавання NP-повна [16]. Завдання залишається NP-повної для дводольних графів [17]. як і для хордальних графів [18].
З позитивних моментів - глибина дерева може бути обчислена за поліноміальний час для інтервальних графів [19]. як і для перестановки графів, трапецеїдальних графів, графів перетинів дуг кіл, циклічних перестановки графів і графів косравнімості обмежених розмірностей [20]. Для неорієнтованих дерев глибина дерева може бути обчислена за лінійний час [21] [22].
Бодлендер, Гілберт, Хафстейнссон і КЛОКС [10] запропонували апроксимаційний алгоритм пошуку глибини дерева c Апроксимаційні коефіцієнтом O ((log n) 2))>. Алгоритм заснований на факті, що глибина дерева логарифмически залежить від деревної ширини графа.
Оскільки глибина дерева монотонна по минорам графа, задача її пошуку фіксовано-параметрически вирішувана [en] - існує алгоритм обчислення глибини дерева, що працює за час f (d) n O (1)>. де d - глибина даного графа і n - число вершин. Таким чином, для будь-якого фіксованого значення d завдання перевірки, не перевищує чи глибина дерева значення d. може бути вирішена за поліноміальний час. Конкретніше - залежність від n в цьому алгоритмі можна зробити лінійної наступним способом: будуємо дерево пошуку в глибину і перевіряємо, більше глибина дерева величини 2 d чи ні. Якщо більше, глибина дерева більше d і задача вирішена. Якщо немає, можна використовувати побудова дерева пошуку на невелику глибину для декомпозиції дерева [en] і стандартну техніку динамічного програмування для графів з обмеженою деревної шириною, щоб обчислити глибину за лінійний час [23].
Можна обчислити глибину дерева точно для графів, значення глибини для яких може бути велике, за час O (cn) з константою c. трохи меншою 2. [24]