Основні відомості з тригонометрії
Відомо, що в геометрії прийнято, розглядаючи прямокутний трикутник, називати сторону, що навпроти прямого кута, гипотенузой. Сторони, що примикають до прямого кута, називаються катетами. Прямий кут має 90 °. Таким чином, на рис. 1 гипотенузой є сторона, позначена літерами Про, катетами ж боку аб і АТ.
На малюнку відзначено, що прямий кут має 90 °, два інші кути трикутника є гострими і позначені літерами # 945; (Альфа) і # 946; (Бета).
Якщо виміряти в певному масштабі боку трикутника і взяти відношення величини катета, що лежить проти кута # 945 ;, до величини гіпотенузи, то таке ставлення називають синусом кута # 945 ;. Синус кута прийнято позначати так: sin # 945 ;. Отже, в прямокутному трикутнику, який ми розглядаємо, синус кута дорівнює:
Якщо скласти відношення, взявши величину катета АТ, що примикає до гострого кута # 945 ;, до гіпотенузи, то це відношення називають косинусом кута # 945; Косинус кута прийнято позначати наступним чином: сos # 945 ;. Таким чином, косинус кута а дорівнює:
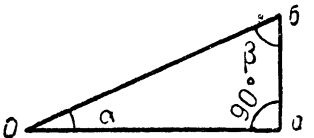
Мал. 1. Прямокутний трикутник.
Знаючи синус і косинус кута # 945 ;, можна визначити величини катетів. Якщо помножити величину гіпотенузи Про на sin # 945 ;, то отримаємо катет аб. Помноживши гіпотенузу на сos # 945 ;, отримаємо катет Оа.
Припустимо, що кут альфа не залишається постійним, а поступово змінюється, збільшуючись. Коли кут дорівнює нулю, синус його також дорівнює нулю, так як нулю район протилежні кутку катет.
У міру того, як кут а буде зростати, почне збільшуватися і його синус. Найбільше значення синуса вийде, коли кут альфа стане прямим, тобто буде дорівнює 90 °. При цьому синус дорівнює одиниці. Таким чином, синус кута може мати найменше значення-0 і найбільше-1. Для всіх проміжних значень кута синус є правильним дробом.
Косинус кута буде найбільшим, коли кут дорівнює нулю. При цьому косинус дорівнює одиниці, так як катет, прилеглий до кута, і гіпотенуза в цьому випадку будуть збігатися один з одним, і відрізки, що зображують їх, рівні між собою. Коли кут дорівнює 90 °, косинус його дорівнює нулю.
Графічні способи зображення змінного струму
Синусоїдальний змінний струм або е.р.с, що змінюються в часі, можна зобразити у вигляді синусоїди. Такий спосіб зображення часто застосовується в електротехніці. Поряд із зображенням змінного струму у вигляді синусоїди широко застосовується також зображення такого струму у вигляді векторів.
Вектором називається величина, що має певне значення і напрямок. Таку величину представляють у вигляді відрізка прямої лінії зі стрілкою на кінці. Стрілка повинна вказувати напрямок вектора, а відрізок, який вимірюється в певному масштабі, дає величину вектора.
Всі фази зміни змінного синусоїдального струму за один період можна зобразити за допомогою векторів, діючи в такий спосіб. Припустимо, що початок вектора знаходиться в центрі кола, а кінець його лежить в самій окружності. Цей вектор, обертаючись у напрямку проти годинникової стрілки, робить повний оборот за час, відповідне одному періоду зміни струму.
Проведемо з точки, що визначає початок вектора, тобто з центру кола О, дві лінії: одну горизонтальну, а іншу вертикальну, як це зображено на рис 2.
Якщо для кожного положення обертового вектора з його кінця, позначеного буквою А, опускати перпендикуляри на вертикальну лінію, то відрізки цієї лінії від точки Про дощенту перпендикуляра а будуть давати нам миттєві значення синусоїдального змінного струму, а сам вектор OA в певному масштабі зображує амплітуду цього струму, тобто його найбільше значення. Відрізки Оа на вертикальній осі називаються проекціями вектора OA на вісь у.
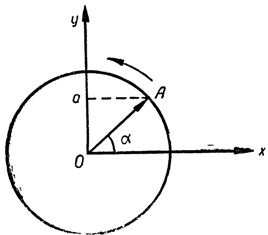
Мал. 2. Зображення змін синусоїдального струму за допомогою вектора.
У справедливості викладеного вище неважко переконатися, виконавши наступну побудову. Поруч з окружністю на малюнку можна отримати синусоїду, відповідну зміни змінної е.р.с. за один період, якщо уздовж горизонтальної лінії відкладати градуси, що визначають фазу зміни е.р.с, а у вертикальному напрямку будувати відрізки, рівні величині проекції вектора OA на вертикальну вісь. Виконавши таке побудова для всіх точок кола, по якій ковзає кінець вектора OA, отримаємо рис. 3.
Повний період зміни струму, а отже, і обертання зображує його вектора, можна уявити не тільки в градусах окружності, а й в радіанах.
Розі в один градус відповідає 1/360 частина кола, описаного з його вершини. Виміряти той чи інший кут в градусах-це значить знайти скільки разів такий елементарний кут міститься в вимірюваному куті.
Однак, при вимірюванні кутів можна користуватися не градусами, а радіанами. При цьому одиницею, з якою порівнюють той чи інший кут, є кут, якому відповідав би дуга, що дорівнює по довжині радіусу будь кола, описаного з вершини вимірюваного кута.
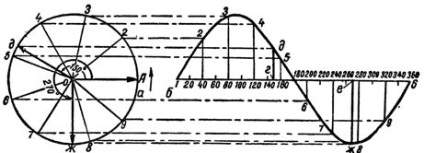
Мал. 3. Побудова синусоїди е.р.с, що змінюється за гармонійним законом.
Таким чином, повний кут, відповідний будь-колу, виміряний в градусах, дорівнює 360 °. Цей же кут, виміряний в радіанах, дорівнює 2 π - 6,28 радіан.
Про становище вектора в даний момент можна судити по кутовий швидкості його обертання і по часу, що минув від початку обертання, тобто з початку періоду. Якщо позначити кутову швидкість вектора буквою # 969; (Омега), а час з початку періоду літерою t, то кут повороту вектора по відношенню до його вихідного положення можна визначити як добуток:
Кут повороту вектора визначає його фазу, якої відповідає той чи інший миттєве значення сили струму. Отже, кут повороту або фазовий кут дозволяє судити про те, яке миттєве значення має сила струму в цікавий для нас момент часу. Фазовий кут часто називають просто фазою.
Вище було показано, що кут повного обороту вектора, виражений в радіанах, дорівнює 2π. Цьому повного обороту вектора відповідає один період зміни змінного струму. Помноживши кутову швидкість # 969; на час T відповідне одному періоду, отримаємо повний оборот вектора змінного струму, виражений в радіанах;
Звідси не важко визначити, що кутова швидкість # 969; дорівнює:
Замінивши період Т ставленням 1 / f, отримаємо:
Кутова швидкість # 969; відповідно до цього математичним співвідношенням часто називається кутовою частотою.
Якщо в колі змінного струму діє не один який-небудь ток, а два або кілька, то їх взаємне співвідношення зручно представляти графічно. Графічне зображення електротехнічних величин (струму, е.р.с. і напруги) можна здійснювати двома способами. Один з цих способів - креслення синусоид, що показують всі фази зміни електротехнічної величини протягом одного періоду. На такому малюнку можна побачити насамперед яке співвідношення максимальних значень досліджуваних струмів, е.р.с. і напруг.
На рис. 4 зображені дві синусоїди, що характеризують зміни двох різних змінних струмів. Ці струми мають однаковий період і збігаються по фазі, але максимальні значення їх різні.
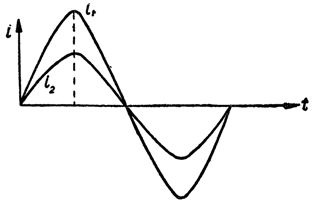
Мал. 4. Синусоїди струмів, що збігаються по фазі.
Струм I1 має велику амплітуду, ніж струм I2. Однак не завжди струми або напруги можуть збігатися по фазі. Часто-густо буває так, що фази у них різні. У цьому випадку говорять, що вони зрушені по фазі. На рис. 5 зображені синусоїди двох струмів, зрушених по фазі.
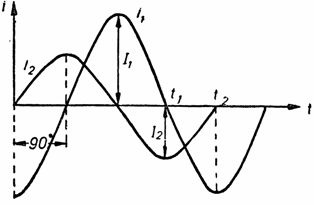
Мал. 5. Синусоїди струмів, зрушених по фазі на 90 °.
Кут зсуву фаз між ними дорівнює 90 °, що становить одну чверть періоду. На малюнку видно, що максимальне значення струму I2 настає раніше на чверть періоду, ніж максимальне значення струму I1. Струм I2 випереджає по фазі струм I1 на чверть періоду, тобто на 90 °. Це ж співвідношення між струмами можна зобразити за допомогою векторів.
На рис. 6 зображені два вектора тих же струмів. Якщо згадати, що напрямок обертання векторів домовилися приймати проти годинникової стрілки, то стає абсолютно очевидним, що вектор струму I2, обертаючись в умовному напрямі йде попереду вектора струму I1. Струм I2 випереджає струм I1. На цьому ж малюнку видно, що кут випередження дорівнює 90 °. Цей кут і є кутом зсуву фаз між I1 і I2. Кут зсуву фаз позначають буквою # 966; (Фі). Такий спосіб зображення електротехнічних величин за допомогою векторів називають векторною діаграмою.
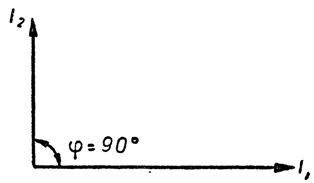
Мал. 6. Векторна діаграма струмів, зрушених по фазі на 90 °.
При кресленні векторних діаграм зовсім не обов'язково зображувати на малюнку окружності, по яких ковзають кінці векторів в процесі уявного нами їх обертання.
Користуючись векторними діаграмами, не слід забувати, що на одній діаграмі можна зображувати тільки електричні величини, які мають однакову частоту, т. Е. Однакову кутову швидкість обертання векторів.