Тип уроку: Узагальнення, закріплення пройденого матеріалу і пояснення нового.
Цілі і завдання уроку:
Обладнання: персональні комп'ютери, мультимедиапроектор, проекційний екран.
Матеріали до уроку: презентація Power Point на комп'ютері вчителя (Додаток 1).
Слайд 1 з додатка 1 (далі посилання на слайди йдуть без вказівки додатка 1).
1. Усна робота (актуалізація знань).
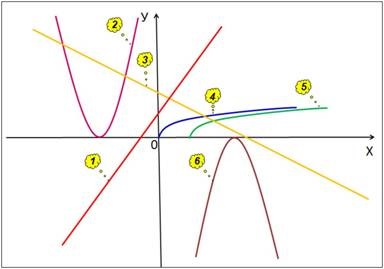
Слайд 2 - Зіставте таких опцій з графіками на кресленні (Рис. 1):
у = 6 - х; у = 2х + 3; у = (х + 3) 2; у = - (х - 4) 2; .
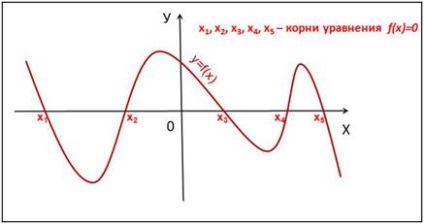
Слайд 3 Графічний спосіб розв'язання рівнянь виду f (x) = 0.
Корінням рівняння f (x) = 0 є значення х1. х2, ... точок перетину графіка функції y = f (x) з віссю абсцис (Рис. 2).
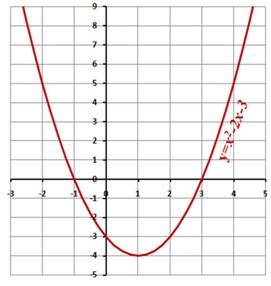
Знайдіть корені рівняння х 2 2х-3 = 0. використовуючи графічний спосіб розв'язання рівнянь (Рис.3).
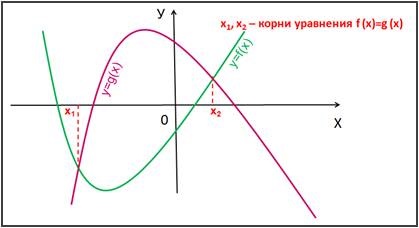
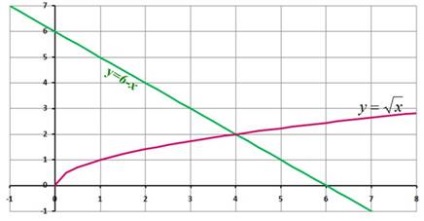
Слайд 5 Графічний спосіб розв'язання рівнянь виду f (x) = g (x).
Корінням рівняння f (x) = g (x) є значення х1. х2, ... точок перетину графіків функцій y = f (x) і у = g (x). (Рис. 4):
Слайд 6 Знайдіть корені рівняння, використовуючи графічний спосіб розв'язання рівнянь (Рис. 5).
2. Пояснення нового матеріалу. Практична робота.
I.Графіческій спосіб вирішення рівнянь виду f (x) = 0 в Excel.
Подальша робота виконується вчителем в Excel одночасно з учнями з докладними (при необхідності) інструкціями і виведенням результатів на проекційний екран. Слайди Додатка 1 використовуються для формулювання завдань і підведення проміжних підсумків.
Приклад 1: Використовуючи засоби побудови діаграм в Excel, вирішити графічним способом рівняння х 2 + 5х-4 = 0.
Для цього: побудувати графік функції у = х 2 + 5х-4 на проміжку [0; 5] з кроком 0,25; \ Знайти значення х точок перетину графіка функції з віссю абсцис.
Виконання завдання можна розбити на етапи:
1 етап: Вивчення функцій в табличній формі (рис. 6):
- в осередок А1 ввести текст Х. в клітинку A2 - Y;
- в осередок В1 ввести число 0, в клітинку С1 - число 0,25;
- виділити осередки В1: С1. підвести покажчик миші до маркера виділення, і в той момент, коли курсор миші прийме форму чорного хрестика, протягнути маркер виділення вправо до комірки V1 (Рис. 7).
Після введення формули в осередку виявиться результат обчислення за формулою, а в поле введення рядка формул - сама формула (Рис. 8):
- скопіювати вміст комірки B2 в осередку C2: V2 за маркер виділення. Весь ряд виділених осередків заповниться вмістом першого осередку. При цьому посилання на осередки в формулах зміняться щодо зміщення самої формули.
2 етап: Побудова діаграми типу Графік.
- виділити діапазон комірок B2: V2;
- на вкладці Вставка | Діаграми | Графік вибрати вид Графік;
- на вкладці Конструктор | Вибрати дані (Рис. 9) у вікні «Вибір джерела даних» клацнути по кнопці Змінити в поле Підписи горизонтальній осі - відкриється вікно «Підписи осі». Виділити в таблиці діапазон комірок B1: V1 (значення змінної х). В обох вікнах клацнути по кнопках ОК;
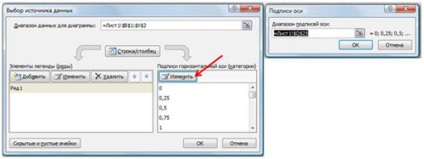
- на вкладці Макет | Осі | Основна горизонтальна вісь | Додаткові параметри основної горизонтальної осі вибрати:
Інтервал між поділами: 4;
Інтервал між підписами: Одиниця виміру інтервалу: 4;
Положення осі: по розподілам;
Вибрати ширину і колір лінії (Виберіть Тип лінії і Колір лінії);
- самостійно змінити ширину і колір лінії для вертикальної осі;
- на вкладці Макет | Сітка | Вертикальні лінії сітки по основній осі вибрати Основні лінії сітки.
Приблизний результат роботи наведено на рис. 10:
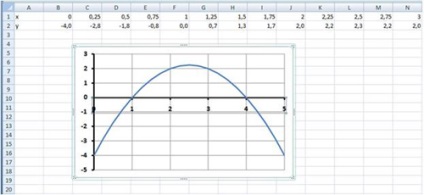
3 етап: Визначення коренів рівняння.
Графік функції у = х 2 + 5х-4 перетинає вісь абсцис в двох точках і, отже, рівняння х 2 + 5х-4 = 0 має два корені: х1 = 1; х2 = 4.
II. Графічний спосіб розв'язання рівнянь виду f (x) = g (x) в Excel.
Приклад 2: Вирішити графічним способом рівняння.
Для цього: в одній системі координат побудувати графіки функцій у1 = і у2 = 1-х на проміжку [-1; 4] з кроком 0,25; знайти значення х точки перетину графіків функцій.
1 етап: Подання функцій в табличній формі (рис. 1):
- Перейти на Аркуш2.
- Аналогічно Прикладу 1. застосувавши прийоми копіювання, заповнити таблицю. При табулюванні функції у1 = скористатися вбудованою функцією Корінь (Рис. 11).
2 етап: Побудова діаграми типу Графік.
Приблизний результат роботи наведено на Рис. 12:
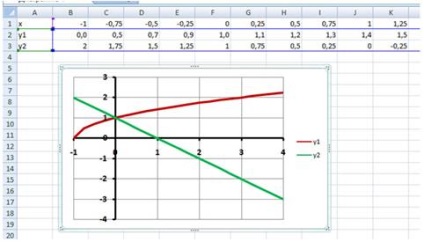
3 етап: Визначення коренів рівняння.
Графіки функцій у1 = і у2 = 1-х перетинаються в одній точці (0; 1) і, отже, рівняння має один корінь - абсциса цієї точки: х = 0.
III.Метод Підбір параметра.
Графічний спосіб розв'язання рівнянь гарний, але далеко не завжди точки перетину можуть бути такими «хорошими», як в спеціально підібраних прикладах 1 і 2.
Можливості електронних таблиць дозволяють знаходити наближені значення коней рівняння з заданою точністю. Для цього використовується метод Підбір параметра.
Приклад 3: Розберемо метод Підбір параметра на прикладі рішення рівняння х 2 + 5х-3 = 0.
1 етап: Побудова діаграми типу Графік для наближеного визначення коренів рівняння.
Побудувати графік функції у = х 2 + 5х-3. відредагувавши отримані в прикладі 1 формули.
- виконати подвійне клацання по комірці B2. внести необхідні зміни;
- за допомогою маркера виділення скопіювати формулу в усі осередки діапазону C2: V2.
Всі зміни відразу відображаються на графіку.
Приблизний результат роботи наведено на Рис. 13:
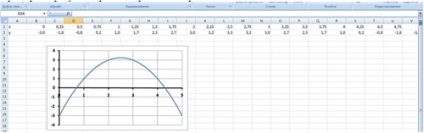
2 етап: Визначення наближених значень коренів рівняння.
Графік функції у = х 2 + 5х-3 перетинає вісь абсцис в двох точках і, отже, рівняння х 2 + 5х-4 = 0 має два корені.
За графіком наближено можна визначити, що х1 ≈0,7; х2 ≈4,3.
3 етап: Пошук наближеного рішення рівняння з заданою точністю методом Підбір параметра.
1) Почати з пошуку більш точного значення меншого кореня.
За графіком видно, що найближчий аргумент до точки перетину графіка з віссю абсцис дорівнює 0,75. У таблиці значень функції цей аргумент розміщується в осередку E1.
- Виділити осередок Е2;
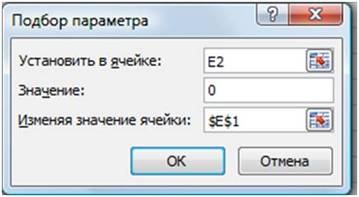
- перейти на вкладку Дані | Аналіз «що-якщо» | Підбір параметра ...;
У діалоговому вікні Підбір параметра (Рис. 14) в поле Значення ввести необхідне значення функції: 0.
В поле Змінюючи значення осередки. ввести $ E $ 1 (клацнувши по осередку E1).
Клацнути по кнопці ОК.
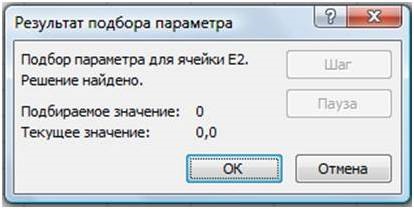
- У вікні Результат підбору (Рис. 15) виводиться інформація про величину подбираемого і підібраного значення функції:
- В осередку E1 виводиться підібране значення аргументу 0,6972 з необхідною точністю (0,0001).
Встановити точність можна шляхом установки в осередках таблиці точності представлення чисел - числа знаків після коми (Формат ячеек | Число | Числовий).
Отже, перший корінь рівняння визначено із заданою точністю: х1 ≈0,6972.
2) Самостійно знайти значення більшого кореня з тією ж точністю. (Х2 ≈4,3029).
IV.Метод Підбір параметра для вирішення рівнянь виду f (x) = g (x).
При використанні методу Підбір параметрів для вирішення рівнянь виду f (x) = g (x) вводять допоміжну функцію y (x) = f (x) -g (x) і знаходять з необхідною точністю значення х точок перетину графіка функції y (x) з віссю абсцис.
3. Закріплення вивченого матеріалу. Самостійна робота.
Завдання: Використовуючи методу Підбір параметрів, знайти корені рівняння з точністю до 0,001.
- ввести функцію у = і побудувати її графік на проміжку [-1; 4] з кроком 0,25 (Рис. 16):
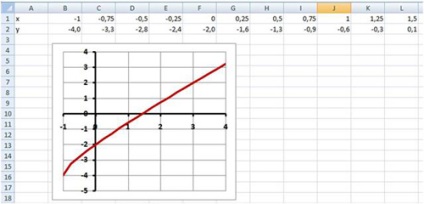
- знайти наближене значення х точки перетину графіка функції з віссю абсцис (х ≈1,4);
- знайти наближене рішення рівняння з точністю до 0,001 методом Підбір параметра (х ≈1,438).
Слайд 12 Перевірка результатів самостійної роботи.
Слайд 13 Повторення графічного способу розв'язання рівняння виду f (x) = 0.
Слайд 14 Повторення графічного способу розв'язання рівняння виду f (x) = g (x).
5. Домашнє завдання.
Використовуючи засоби побудови діаграм в Excel і метод Підбір параметра, визначте корені рівняння х 2 -5х + 2 = 0 з точністю до 0,01.