Землю в першому наближенні можна вважати кулею. У другому наближенні Землю беруть за еліпсоїд обертання; в деяких дослідженнях її вважають двохосьовим еліпсоїдом. Геоід- тіло прийняте за теоретичну фігуру Землі, обмежена поверхнею океанів в їх спокійному стані, продовженої і під материками, З огляду на нерівномірність розподілу мас в земній корі геоид має неправильну геометричну форму, і його поверхня не можна виразити математично, що необхідно для вирішення геодезичних завдань . При вирішенні геодезичних завдань геоид замінюють близькими до нього геометрично правильними поверхнями. Так, для наближених обчислень Землю беруть за кулю з радіусом 6371 км. Ближче до форми геоїда підходить еліпсоїд - фігура, що отримується обертанням еліпса (рис. 2.1) навколо його малої осі. Розміри земного еліпсоїда характеризують такими основними параметрами: a велика піввісь, b мала піввісь, полярне стиснення і e - перший ексцентриситет меридіанного еліпса, де і.
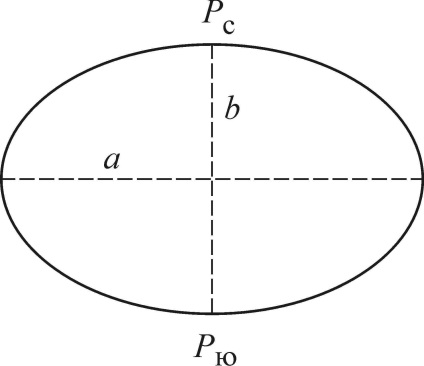
Мал. 2.1. Меридіанний еліпс: Рс - північний полюс; Рю - південний полюс
Розрізняють загальземного еліпсоїд і референц-еліпсоїд.
Референц-еліпсоїд - еліпсоїд, прийнятий для геодезичних робіт в конкретній країні. З референц-еліпсоїдом пов'язана прийнята в країні система координат. Параметри референц-еліпсоїда підбираються під умовою найкращої апроксимації даної частини поверхні Землі. При цьому поєднання центрів еліпсоїда і Землі не досягають.
У Росії з 1946 р в якості референц-еліпсоїда використовується еліпсоїд Красовського з параметрами: а = 6 378 245 м, a = 1 / 298,3.
2. Система координат в геодезії. Абсолютні і відносні висоти.
Системи координат, що застосовуються в геодезії
Для визначення положення точок в геодезії застосовують просторові прямокутні, геодезичні і плоскі прямокутні координати.
Просторові прямокутні координати. Початок системи координат розташовано в центрі O земного еліпсоїда (рис. 2.2).
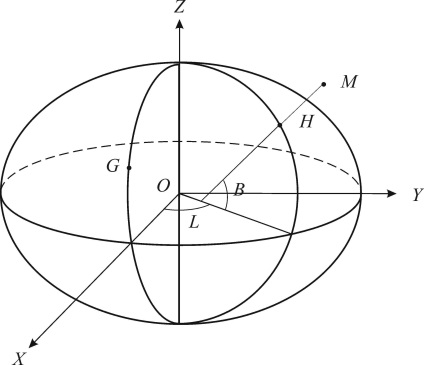
Мал. 2.2. Земний еліпсоїд і координати: Х. Y. Z - просторові прямокутні; B. L, H геодезичні; G Грінвіч
Вісь Z спрямована по осі обертання еліпсоїда на північ. ОсьХ лежить в перетині площині екватора з начальнимгрінвічскім меридіаном. ОсьY спрямована перпендикулярно осямZ иx на схід.
Геодезичні координати. Геодезичними координатами точки є її широта, довгота і висота (рис. 2.2).
Геодезичної шіротойточкіМ називається уголВ. утворений нормаллю до поверхні еліпсоїда, що проходить через дану точку, і площиною екватора.
Широта відраховується від екватора на північ і південь від 0до 90і називається північній або південній. Північну широту вважають позитивною, а южнуюотріцательной.
Площині перетину еліпсоїда, що проходять через вісь OZ. називаютсягеодезіческімі меридіанами.
Геодезичної довготою точки називається двогранний уголL. утворений площинами початкового (за Гринвічем) геодезичного меридіана і геодезичного меридіана даної точки.
Довготу відраховують від початкового меридіана в межах від 0до 360на схід, або від 0до 180на схід (позитивні) і від 0до 180на захід (негативні).
Геодезичної висотою точки є її висотаН над поверхнею земного еліпсоїда.
Геодезичні координати з просторовими прямокутними координатами пов'язані формулами
де e первий ексцентриситет меридіанного еліпса іN радіус кривизни першого вертикалі. При етомN = a / (1e 2 sin 2 B) 1/2. Геодезичні та просторові прямокутні координати точок визначають за допомогою супутникових вимірювань, а також шляхом їх прив'язки геодезичними вимірами до точок з відомими координатами. Відзначимо, що поряд з геодезичними існують ще астрономічні широта і долгота.Астрономіческая широта етоугол, складений прямовисною лінією в даній точці з площиною екватора.Астрономіческая довгота - кут між площинами Гринвічського меридіана і проходить через прямовисну лінію в даній точці астрономічного меридіана. Астрономічні координати визначають на місцевості з астрономічних наблюденій.Астрономіческіе координати відрізняються від геодезичних тому, що напрямки стрімких ліній не збігаються з напрямками нормалей до поверхні еліпсоїда. Кут між напрямком нормалі до поверхні еліпсоїда і прямовисною лінією в даній точці земної поверхні називається ухиленням прямовисній лінії.
Узагальненням геодезичних і астрономічних координат є термін - географічні координати.
Плоскі прямокутні координати. Для вирішення завдань інженерної геодезії від просторових і геодезичних координат переходять до більш простим - плоским координатами, що дозволяє зображати місцевість на площині і визначати положення точок двома координатами х і у.
Оскільки опуклу поверхню Землі зобразити на площині без спотворень можна, введення плоских координат можливо тільки на обмежених ділянках, де спотворення настільки малі, що ними можна знехтувати. У Росії прийнята система прямокутних координат, основою якої є рівнокутна поперечно-циліндрична проекція Гаусса. Поверхня еліпсоїда зображується на площині по частинах, званим зонами. Зони є сферичні Двуугольнік, обмежені меридіанами, і тягнуться від північного полюса до південного (рис. 2.3). Розмір зони по довготі дорівнює 6. Центральний меридіан кожної зони називається осьовим. Нумерація зон йде від Грінвіча на схід.
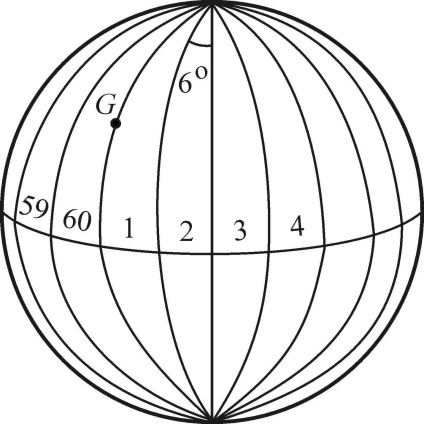
Мал. 2.3. Розподіл поверхні Землі на координатні зони: G - Грінвіч