Даний алгоритм за рішенням судоку 9x9 надіслав наш регулярний гравець Олександр Кузнєцов (alex_tlt)
Пропоную увазі любителів судоку свій алгоритм вирішення цієї захоплюючої задачі. Відразу обмовлюся, що алгоритм не найшвидший, а деякі прийоми рішення свідомо опущені.
Моя мета - показати алгоритм, тобто, послідовність дій, яка обов'язково призведе до успіху.
Як приклад використовується судоку № 3448. Алгоритм складається з чотирьох пунктів.
- Пошук єдиною порожній клітини в рядку, стовпці, квадраті.
- Пошук єдиною обраної цифри в квадраті.
- Пошук єдино допустимого варіанту з решти в рядку, стовпці, квадраті (останній кандидат).
- Рішення альтернатив.
1. Якщо в рядку, стовпці або квадраті заповнені 8 клітин, то в дев'яту, порожню клітину треба вписати відсутню цифру. Якщо при цьому виявиться, що в великому квадраті 9х9 порожніх клітин не залишилося, судоку вважається вирішеним. Цей пункт не вимагає ілюстрацій, його я включив тільки для дотримання повноти алгоритму.
2. Квадрат вигідно відрізняється від рядків і стовпців своєю компактністю. Тому доцільно починати рішення саме з квадратів. Вибираємо будь-яку цифру від 1 до 9 і подумки проектуємо заповнені цифри на ті квадрати, в яких обраної цифри немає. Переважно починати з самої часто зустрічається в умови цифри. Якщо ж не враховувати цей фактор, починаємо з цифри 1.
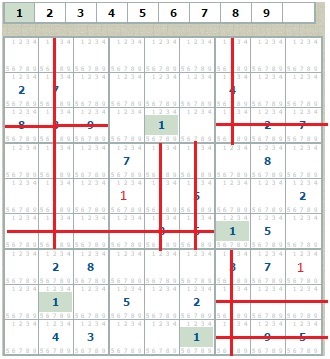
Чотири одиниці (вони виділені фоном) проектуються на 5 квадратів, що не містять цю цифру. Відразу ж виявляються єдині порожні клітини в середньому квадраті і нижньому правому квадраті.
Заповнюємо ці клітини одиницями:
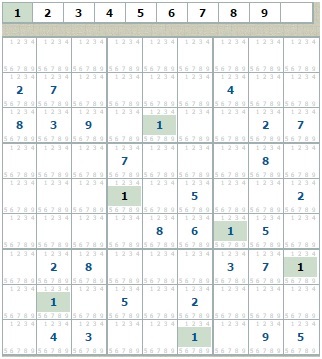
Продовжуємо пошук в останніх квадратах цифри 1 з урахуванням знайдених.
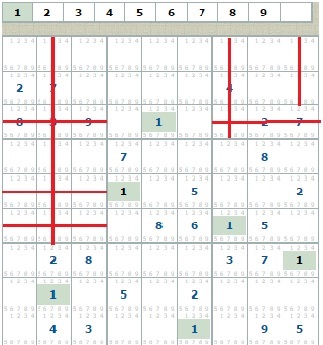
Нових одиниць, не знайдено. Переходимо до наступної цифри 2, буде знайдена одна двійка. Малюнок не наводжу, щоб не захаращувати документ. Переходимо до наступних цифр, будуть знайдені трійка, п'ятірка, сімки. Що стосується вісімок, ілюстрація просто необхідна!
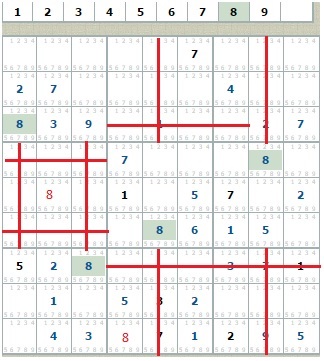
Чотири вісімки проектуються на 5 квадратів, що не містять цю цифру. Єдині порожні клітини виявляються в нижньому середньому квадраті і в середньому лівому. Причому останній - абсолютно порожній! Це ще раз підкреслює висловлене раніше положення про компактності квадратів. У нашому випадку достатнім виявилося чотири цифри, щоб закрити вісім порожніх клітин.
Далі, після того як знаходити цифри 9 судоку набуває такого вигляду:
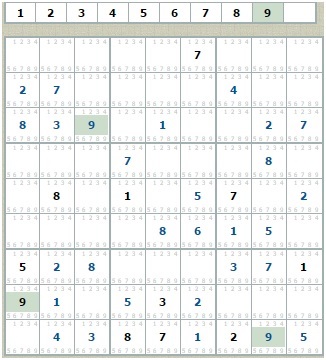
Тепер необхідно застосувати пункт 1 (його завжди потрібно тримати в умі) послідовно для самої нижньої рядки, де бракує шістки, а потім для нижнього лівого квадрата, де бракує сімки.
Повертаємося до пункту 2 і відновлюємо пошук з цифри 1. В даному алгоритмі пункт 2 повинен закінчитися тільки тоді, коли перебір всіх 9-ти цифр не дасть жодного позитивного рішення.
Переходимо до пункту 3.
3. У третій зверху рядку залишилися незаповненими три клітини-кандидата з цифрами 4, 5, 6 (сірі цифри). У шостому стовпці вже є 5 і 6, отже залишається варіант 4 - останній кандидат.
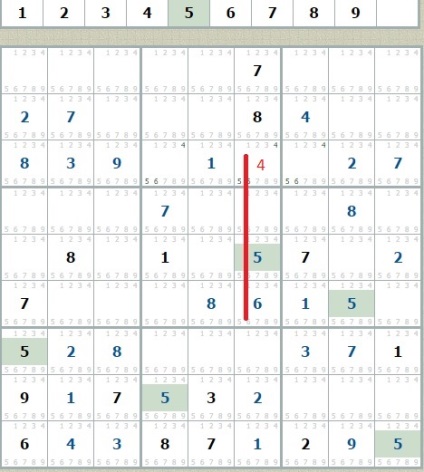
Складні судоку, як правило, не обходяться без пункту 4 «Альтернативи». Розберемо цей випадок стосовно судоку № 3448, допустивши що на певному етапі ми не змогли обійтися п.п. 1-3.
4. У самому лівому стовпці залишилися незаповненими дві клітини, значення яких можуть бути або 1, або 4, і вони відзначені сірими цифрами. В цьому випадку припускаємо, що 1 знаходиться у верхній клітці і натискаємо кнопку «Зберегти».
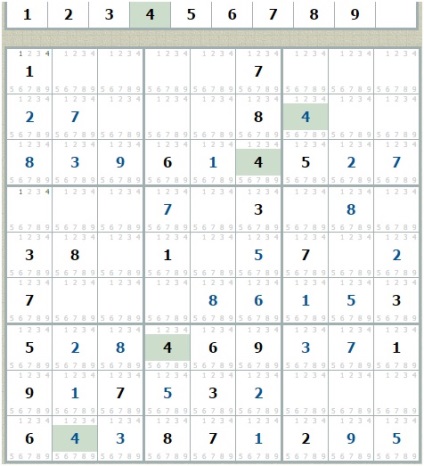
Після того, як СУДК збережений, в альтернативній клітці ставимо 4 і виконуємо пункт 2 «Пошук по квадратах».
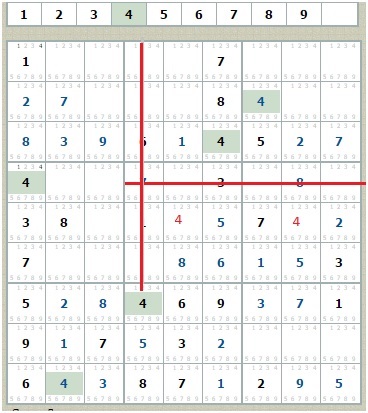
В результаті приходимо до протиріччя: п'ята зверху рядок містить дві однакові цифри 4. Зауважу, що при рішення альтернатив протиріччя є найбільш бажаним результатом! Тепер залишається натиснути кнопку «Завантажити» і в збереженому судоку у верхній клітці замість 1 поставити 4, а в альтернативній 1.
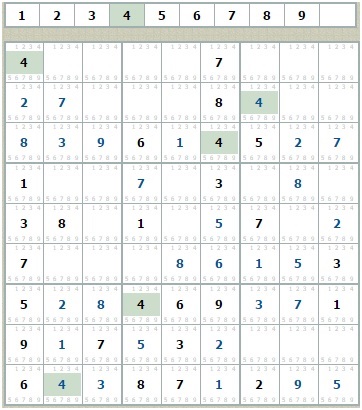
А далі знову повторення пунктів 1-3, які приведуть до правильного рішення. Успіхів!
svnnvs Online 1 4 сайті: 18 місяців
"Складні судоку, як правило, не обходяться без пункту 4« Альтернативи »" - як-то це не красиво!