Як побудувати графік по n точкам? Найпростіше - відзначити їх маркерами на координатної сітки. Однак для наочності їх хочеться з'єднати, щоб отримати легко читається лінію. З'єднувати точки найпростіше відрізками прямих. Але графік-ламана читається досить важко: погляд чіпляється за кути, а не ковзає уздовж лінії. Та й виглядають злами не дуже красиво. Виходить, що крім ламаних потрібно вміти будувати і криві. Однак тут потрібно бути обережним, щоб не вийшло ось такого:
трохи матчастини
Відновлення проміжних значень функції, яка в даному випадку задана таблично у вигляді точок P1 # 038; nbsp ... # 038; nbspPn. називається інтерполяцією. Є безліч способів інтерполяції, але всі вони можуть бути зведені до того, що треба знайти n # 038; nbsp- # 038; nbsp1 функцію для розрахунку проміжних точок на відповідних сегментах. При цьому задані точки обов'язково повинні бути обчислюваності через відповідні функції. На основі цього і може бути побудований графік:
Функції fi можуть бути самими різними, але найчастіше використовують поліноми деякій мірі. В цьому випадку підсумкова інтерполююча функція (кусочно задана на проміжках, обмежених точками Pi) називається сплайном.
ставимо досліди
Найпростіший приклад - лінійна інтерполяція, в якій використовуються поліноми першого ступеня, а в підсумку виходить ламана, що з'єднує задані точки.
Давайте додамо трохи конкретики. Ось набір точок (взяті майже зі стелі):
Результат лінійної інтерполяції цих точок виглядає так:
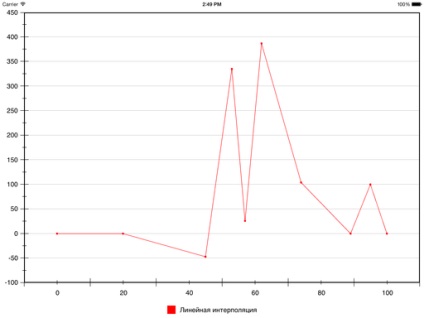
Однак, як зазначалося вище, іноді хочеться отримати в результаті гладку криву.
Що є гладкість? Побутовий відповідь: відсутність гострих кутів. Математичний: безперервність похідних. При цьому в математиці гладкість має порядок, рівний номеру останньої безперервної похідної, і область, на якій ця безперервність зберігається. Тобто, якщо функція має гладкість порядку 1 на відрізку [a; # 038; nbspb], це означає, що на [a; # 038; nbspb] вона має безперервну першу похідну, а ось друга похідна вже терпить розрив в якихось точках.
У сплайна в контексті гладкості є поняття дефекту. Дефект сплайна - це різниця між його ступенем і його гладкістю. Ступінь сплайна - це максимальний ступінь використаних в ньому полиномов.
Важливо відзначити, що «небезпечними» точками у сплайна (в яких може порушитися гладкість) є якраз Pi. тобто точки зчленування сегментів, в яких відбувається перехід від одного полінома до іншого. Всі інші точки «безпечні», адже у полінома на області його визначення немає проблем з безперервністю похідних.
Щоб домогтися гладкої інтерполяції, потрібно підвищити ступінь поліномів і підібрати їх коефіцієнти так, щоб в граничних точках зберігалася безперервність похідних.
Традиційно для вирішення такого завдання використовують поліноми третього ступеня і домагаються безперервності першої і другої похідної. Те, що виходить, називають кубічним сплайном дефекту 1. Ось як він виглядає для наших даних:
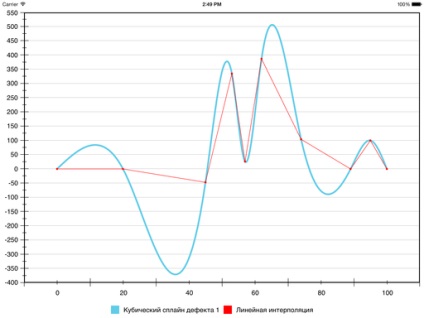
Крива, дійсно, гладка. Але якщо припустити, що це графік деякого процесу або явища, який потрібно показати зацікавленій особі, то такий метод, швидше за все, не підходить. Проблема в помилкових екстремуму. З'явилися вони через надто сильного викривлення, яке було покликане забезпечити гладкість інтерполяційної функції. Але глядачеві таку поведінку зовсім недоречно, адже він виявляється обдурять щодо пікових значень функції. А заради наочної візуалізації цих значень, власне, все й затівалося.
Так що треба шукати інші рішення.
Інша традиційне рішення, крім кубічних сплайнів дефекту 1 - поліноми Лагранжа. Це поліноми ступеня n # 038; nbsp- # 038; nbsp1, які беруть задані значення в заданих точках. Тобто членування на сегменти тут не відбувається, вся послідовність описується одним поліномом.
Але ось що виходить:
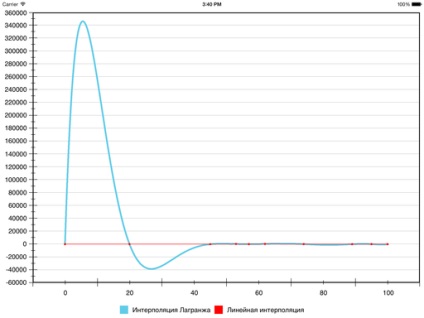
Гладкість, звичайно, присутній, але наочність постраждала так сильно, що ... мабуть, варто пошукати інші методи. На деяких наборах даних результат виходить нормальний, але в загальному випадку помилка щодо лінійної інтерполяції (і, відповідно, помилкові екстремуми) може виходити занадто великий - через те, що тут всього один поліном на всі сегменти.
У комп'ютерній графіці дуже широко застосовуються криві Безьє. представлені поліномами k-го ступеня.
Вони не є інтерполюються, так як з k # 038; nbsp + # 038; nbsp1 точок, що беруть участь в побудові, підсумкова крива проходить лише через першу і останню. решта k # 038; nbsp- # 038; nbsp1 точок грають роль свого роду «гравітаційних центрів», що притягують до себе криву.
Ось приклад кубічної кривої Безьє:
Як це можна використовувати для інтерполяції? На основі цих кривих теж можна побудувати сплайн. Тобто на кожному сегменті сплайна буде своя крива Безьє k-го ступеня (до речі, k # 038; nbsp = # 038; nbsp1 дає лінійну інтерполяцію). І питання тільки в тому, яке k взяти і як знайти k # 038; nbsp- # 038; nbsp1 проміжну крапку.
Тут нескінченно багато варіантів (оскільки k нічим не обмежена), однак ми розглянемо класичний: k # 038; nbsp = # 038; nbsp3.
Щоб підсумкова крива була гладкою, потрібно домогтися дефекту 1 для складається сплайна, тобто збереження безперервності першої і другої похідних в точках зчленування сегментів (Pi), як це робиться в класичному варіанті кубічного сплайна.
Вирішення цього завдання детально (з вихідним кодом) розглянуто тут.
Ось що вийде на нашому тестовому наборі:
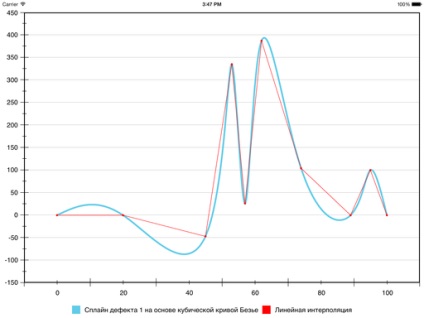
Стало краще: помилкові екстремуми все ще є, але хоча б не так сильно відрізняються від реальних.
Думаємо і експериментуємо
Можна спробувати послабити умову гладкості: зажадати дефект 2, а не 1, тобто зберегти безперервність однієї тільки першої похідної.
Достатня умова досягнення дефекту 2 в тому, що проміжні контрольні точки кубічної кривої Безьє, суміжні із заданою точкою інтерпольованої послідовності, лежать з цією точкою на одній прямій і на однаковій відстані:
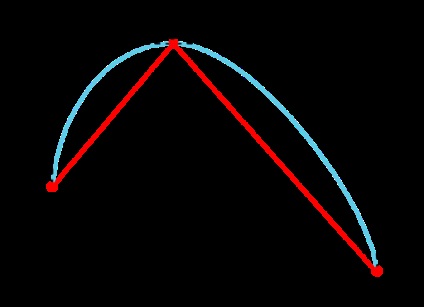
Як прямих, на яких лежать точки Ci # 038; nbsp- # 038; nbsp1 (2). Pi і Ci (1). доцільно взяти дотичні до графіка інтерпольованої функції в точках Pi. Це гарантує відсутність помилкових екстремумів, так як крива Безьє виявляється обмеженою ламаної, побудованої на її контрольних точках (якщо ця ламана не має самоперетинів).
Методом проб і помилок евристика для розрахунку відстані від точки інтерпольованої послідовності до проміжної контрольної вийшла такою:

Перша і остання проміжні контрольні точки рівні першої та останньої точки графіка відповідно (точки C1 (1) і Cn # 038; nbsp- # 038; nbsp1 (2) збігаються з точками P1 і Pn відповідно).
В цьому випадку виходить ось така крива:
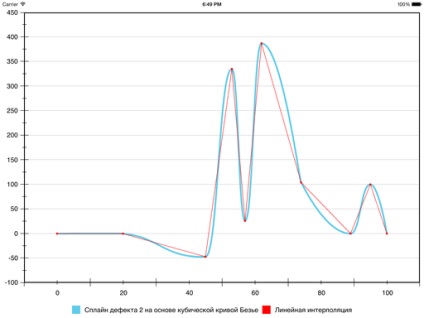
Як видно, помилкових екстремумів вже немає. Однак якщо порівнювати з лінійною інтерполяцією, місцями помилка дуже велика. Можна зробити її ще менше, але тут в хід підуть ще більш хитрі евристики.
До поточного варіанту ми прийшли, зменшивши гладкість на один порядок. Можна зробити це ще раз: нехай сплайн матиме дефект 3. За фактом, тим самим формально функція не гладкою взагалі: навіть перша похідна може терпіти розриви. Але якщо рвати її акуратно, візуально нічого страшного не станеться.
Відмовляємося від вимоги рівності відстаней від точки Pi до точок Ci # 038; nbsp- # 038; nbsp1 (2) і Ci (1). але при цьому зберігаємо їх все лежать на одній прямій:
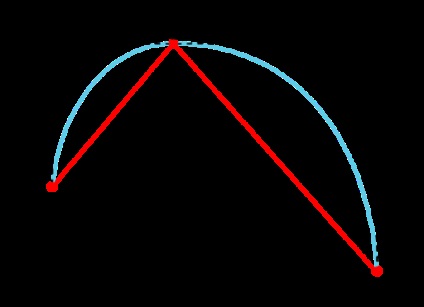
Евристика для обчислення відстаней буде такою:
Розрахунок l1 і l2 такий же, як в «евристиці 1».
При цьому, однак, варто ще перевіряти, чи не збіглися точки Pi і Pi # 038; nbsp + # 038; nbsp1 по ординате, і, якщо співпали, вважати l1 # 038; nbsp = # 038; nbspl2 # 038; nbsp = # 038; nbsp0. Це захистить від «спухання» графіка на плоских відрізках (що теж важливо з точки зору правдивого відображення даних).
Результат виходить такий:
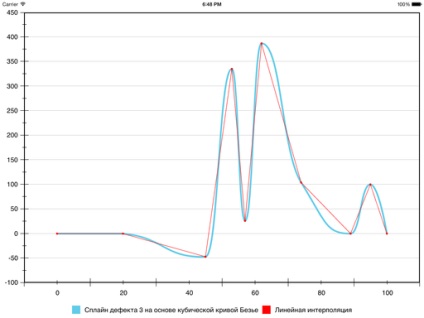
В результаті на шостому сегменті помилка зменшилася, а на сьомому - збільшилася: кривизна у Безьє на ньому виявилася більшою, ніж хотілося б. Виправити ситуацію можна, примусово зменшивши кривизну і тим самим «притиснувши» Безьє ближче до відрізка прямої, яка з'єднує граничні точки сегмента. Для цього використовується наступна евристика:
Якщо абсциса точки перетину дотичних в точках Pi (xi, # 038; nbspyi) і Pi # 038; nbsp + # 038; nbsp1 (xi # 038; nbsp + # 038; nbsp1, # 038; nbspyi # 038; nbsp + # 038; nbsp1) лежить в відрізку [xi; # 038; nbspxi # 038; nbsp + # 038; nbsp1], то l1 або l2 вважаємо рівним нулю. У тому випадку, якщо дотична в точці Pi спрямована вгору, нулю вважаємо максимальне з l1 і l2. якщо вниз - мінімальне.
На цьому було прийнято рішення визнати мету досягнутою.
Може бути, комусь стане в нагоді код.
А як люди щось роблять?
Обіцяний огляд. Звичайно, перед вирішенням завдання ми подивилися, хто чим може похвалитися, а вже потім почали розбиратися, як зробити самим і по можливості краще. Але ось як тільки зробили, не без задоволення ще раз пройшлися по доступним інструментам і порівняли їх результати з плодами наших експериментів. Отже, поїхали.
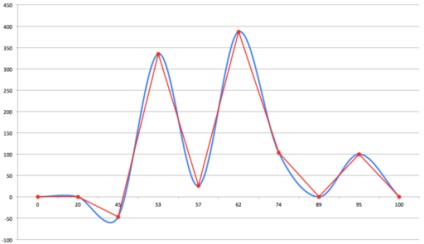
Це дуже схоже на розглянутий вище сплайн дефекту 1, заснований на кривих Безьє. Правда, на відміну від нього в чистому вигляді, тут всього два неправдивих екстремуму - перший і другий сегменти (у нас було чотири). Мабуть, до класичного пошуку проміжних контрольних точок тут додаються ще якісь евристики. Але від усіх помилкових екстремумів вони не врятували.
LibreOffice Calc
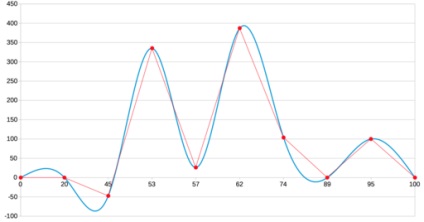
В налаштуваннях це названо кубічним сплайном. Очевидно, він теж заснований на Безьє, і ось тут вже точна копія нашого результату: всі чотири хибних екстремуму на місці.
Є там ще один тип інтерполяції, який ми тут не розглядали: B-сплайн. Але для нашої задачі він явно не підходить, так як дає ось такий результат 🙂
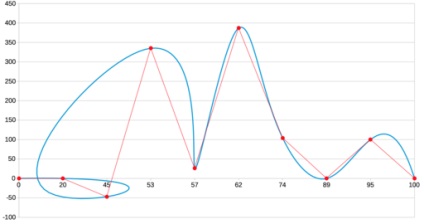
Highcharts. одна з найпопулярніших JS-бібліотек для побудови діаграм
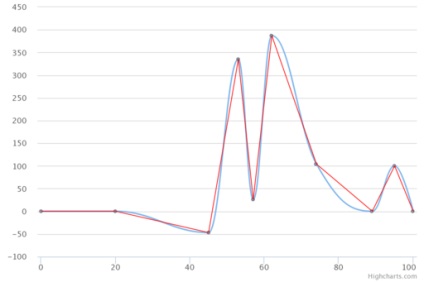
Тут бачимо «метод дотичних» в варіанті рівності відстаней від точки інтерпольованої послідовності до проміжних контрольних. Помилкових екстремумів немає, зате є порівняно велика помилка щодо лінійної інтерполяції (сьомий сегмент).
amCharts. ще одна популярна JS-бібліотека
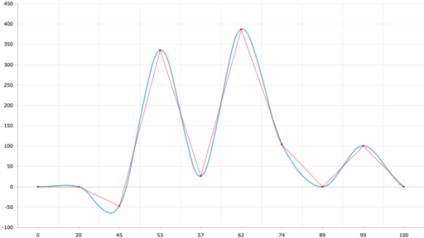
Картина дуже схожа на екселевскій, ті ж два неправдивих екстремуму в тих же місцях.
Coreplot. найпопулярніша бібліотека побудови графіків для iOS і OS X
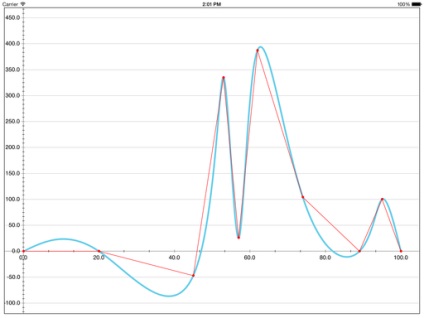
Є помилкові екстремуми і видно, що використовується сплайн дефекту 1 на основі Безьє.
Бібліотека відкрита, так що можна подивитися в код і переконатися в цьому.
aChartEngine. ніби як найпопулярніша бібліотека побудови графіків для Android
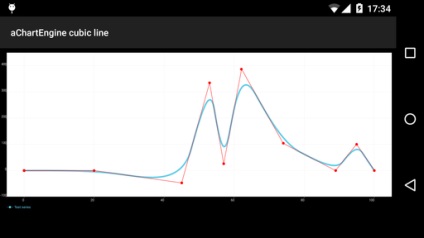
Найбільше схоже на криву Безьє ступеня n # 038; nbsp- # 038; nbsp1, хоча в самій бібліотеці графік називається «cubic line». Дивно! Як би там не було, тут не тільки присутні помилкові екстремуми, а й в принципі не виконуються умови інтерполяції.
замість висновку
В остаточному підсумку виходить, що з «великих хлопців» краще за всіх проблему вирішили Highcharts. Але метод, описаний в цій статті, забезпечує ще меншу помилку щодо лінійної інтерполяції.
Взагалі, зайнятися цим довелося на прохання покупців, які зарепортілі нам «гострі кути» в якості бага в нашому движку діаграм. Будемо раді, якщо описаний досвід комусь стане в нагоді.