Інтерполяція малюємо плавні графіки за допомогою кривих Безьє

Доброго времени суток, харбачітатель.

Постановка задачі
Є масив Y-ков точок, розташованих рівномірно по осі X. Потрібно отримати плавний графік, який проходить через всі задані точки. Приклад на малюнку нижче:

Інтерполяція малюємо плавні графіки за допомогою кривих Безьє

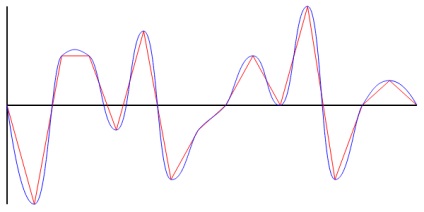
Всіх, кому цікаво, прошу під кат.

Існує ряд стандартних рішень для проведення плавною кривою через точки (з цього приводу багато цікавого написано в уже згаданій статті) таких, як наприклад, інтерполяції сплайнами. Коли на третьому курсі був придуманий цей алгоритм, слово «інтерполяція» вселяло в мене жах, а гугленіе за запитом «згладжування графіків» не давало посильних розуміння результатів. Але якось я дійшов до кривих Безьє і вже дуже вони мені сподобалися. Малює швидко, алгоритм інтуїтивно зрозумілий ... Що ще треба для щастя. Ну і якось понеслося.

Основна ідея

Розіб'ю ідею на три підпункти, щоб було зрозуміліше і читабельними.

Відстань від точки А до точок B1 і C1 було вирішено взяти рівним половині кроку по X між точками B і A. A і C. і т.д. Мені складно якось обґрунтувати такий вибір, але важливо, щоб ця відстань була менше, ніж крок по X між точками А і B. інакше може вийде щось таке, як на малюнку нижче. Важливо розуміти, що чим більше буде ця відстань, тим більше звивистій буде крива і навпаки. Відстань в половину кроку по X мені здається оптимальним, але тут вже можливі варіанти.

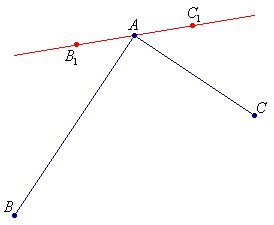
Таким чином виходить, що завдання зводиться до пошуку прямий (B1 C1) і, власне, опорних точок B1 і C1. за якими ми потім будемо будувати криві Безьє.

Пошук прямий

Як відомо, пряма на площині виражається формулою y = kx + b. де k - тангенс кута нахилу прямої до осі Х. Коли ми знайдемо k. то знаючи, що пряма проходить через точку А. і знаючи її координати, ми легко можемо знайти b. b = YA -kXA. Таким чином все зводиться до пошуку коефіцієнта k.

Пошук коефіцієнта k

Скажу наперед, що k = tg (φ) = tg ((α-β) / 2) = (Sqrt ((ΔX 2 + (YA -YB) 2) * (ΔX 2 + (YA -YC) 2)) - ΔX 2 - (YA -YB) * (YA -YC)) / (ΔX * ((YA -YB) - (YA -YC))). де ΔX - відстань по Х між точками (нагадаю, що у нас точки розташовані рівномірно по Х). Нижче представлено математичне доказ правильності формули, але якщо ви не в настрої, то можете його просто пропустити.

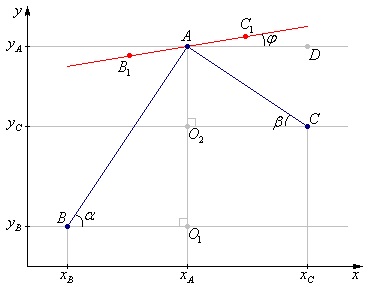
Математичне виведення коефіцієнта k

(6) ∠C1 AС = ∠C1 AD + ∠DAC = φ + ∠DAC
(7) ∠DAC = ∠O2 CA = β - як внутрішні різносторонні кути утворені двома паралельними прямими (AD) і (O2 C) і січною (AC)

Під квадратними дужками мається на увазі довжина відрізка (не хотів використовувати вертикальні прямі - сподіваюся, що читач мене простить)

З попереднього підпункту слід:

І так, k ми знайшли; b ми теж знаємо (дивись вище), а значить пряма, на якій лежать опорні точки, нам відома.

Шукаємо опорні точки

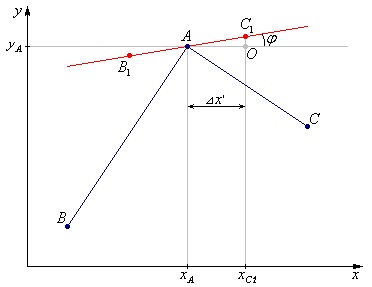
Трохи математики, яка це доводить

З тригонометрії ми пам'ятаємо, що:

Якщо ми приймаємо [AC1] рівним половині кроку по X між основним точками графіка (точками B і A. A і C. т.д.), то:

До приємного!

Приклад реалізації на JSFiddle