У статті розглядається проблема розгортання програмно-визначених компонент в # xa0; вже існуючу мережу. Дається формулювання проблеми оптимізації контролера програмно визначається мережі і # xa0; математичний опис на основі прямо-двоїстого алгоритму.
Програмно-яка визначається мережу # xa0; - це ідеологія побудови мережі, в # xa0; якій розділені рівень управління мережею і # xa0; рівень пересилання пакетів. Загальним для всіх підходів побудови програмно-визначених є те, що програмно-обумовлена мережа складається з двох основних компонентів:
- # xa0; Контролер програмно-яка визначається мережі (КС). КС є логічно централізовану функцію [1], [2]. Мережа, як правило, контролюється одним або декількома КС. КС визначає шлях пересилання для кожного потоку в # xa0; мережі;
- # xa0; Елемент пересилання програмно-яка визначається мережі (ЕП). ЕП утворюють рівень передачі даних в # xa0; мережі. Логіка пересилання пакетів визначається КС і # xa0; реалізується в # xa0; таблиці пересилання.
Проблема інжинірингу трафіку полягає в # xa0; тому, що в # xa0; ймовірний сценарій програмно-які визначаються компоненти будуть поступово розгортатися в # xa0; вже існуючої мережі. В # xa0; такої мережі не обов'язково весь трафік управляється одним КС. Там може бути кілька КС для різних частин мережі, а # xa0; також деякі частини мережі можуть використовувати вже існуючу маршрутизацію в # xa0; мережі. Ключове питання полягає в # xa0; тому, що ще можна зробити ефективним в # xa0; управлінні трафіком, коли весь трафік в # xa0; мережі не може управлятися централізовано одним КС.
Рассматріваемаясеть містить центральний КС, який обчислює таблиці маршрутизації для ряду ЕП. Передбачається, що ЕП є підмножиною вузлів в # xa0; мережі. Решта вузли в # xa0; мережі запускають певний стандартний hop-by-hop протокол маршрутизації (наприклад OSPF). КС переглядає мережу і # xa0; збирає інформацію про # xa0; стан каналу зв'язку. Пакети маршрутизації ЕП і # xa0; логіка для обчислення таблиці маршрутизації на ЕП знаходиться в # xa0; централізованому КС. В # xa0; доповнення до # xa0; пересилання пакетів, ЕП виконує деякі прості вимірювання трафіку, які передаються КС. КС використовує цю інформацію про # xa0; трафіку разом з # xa0; інформацією, що розповсюджується в # xa0; мережі з # xa0; допомогою протоколу OSPF-TE, щоб динамічно змінювати таблиці маршрутизації на ЕП з # xa0; метою адаптації до # xa0; мінливих станів трафіку. Звичайні вузли мережі є стандартними маршрутизаторами, які використовують звичайний hop-by-hop механізм маршрутизації [3]. Передбачається, що ніякі зміни не будуть внесені в # xa0; звичайні вузли і # xa0; вони можуть не знати про # xa0; існування ЕП в # xa0; мережі.
Приклад мережі з # xa0; КС і # xa0; елементами пересилання показаний на Рис. 1. Елементи пересилання в # xa0; вузлах 2, 9, 14 управляються КС ззовні. Дана мережа буде використовуватися для ілюстрації концепцій, висунутих в # xa0; даній роботі. Для простоти вважаємо, що всі з'єднання в # xa0; мережі є двонаправленими і # xa0; ваги ліній зв'язку встановлюються в # xa0; одиницю. Тепер опишемо КС і # xa0; ЕП більш докладно.
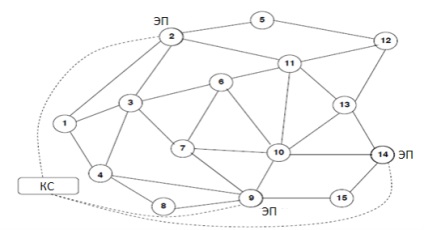
1.1 Елемент пересилання програмно-яка визначається мережі
ЕП виконує наступні функції:
Пересилання: ЕП діють в # xa0; основному в # xa0; як елементи маршрутизації. Таблиця маршрутизації обчислюється на КС [4]. ЕП може обробляти кілька наступних переходів для даного вузла призначення. За наявності кількох наступних переходів до даного вузла призначення, то ЕП може розділити трафік до # xa0; місця призначення в # xa0; заздалегідь встановленому порядку на кілька наступних вузлів.
1.2 Контролер програмно-яка визначається мережі
КС виконує всю логіку маршрутизації і # xa0; координує маршрутизацію на всіх ЕП для того, щоб досягти оптимальної роботи мережі. КС виконує наступні функції:
Обчислення маршруту: КС відповідає за обчислення таблиць маршрутизації для всіх ЕП в # xa0; мережі. Обчислення відбувається з # xa0; урахуванням маршрутизації, що здійснюється на звичайних вузлах (на основі ваг ліній зв'язку OSPF), трафік по лініях зв'язку (на основі інформації OSPF-TE) і # xa0; поточний шаблон трафіку (на основі вимірів на ЕП). Алгоритм для обчислення маршрутизації для ЕП повинен гарантувати, що маршрутизація буде відбуватися по шляхах без петель при одночасній мінімізації перевантаження мережі.
2. Постановка завдання КС
Проілюструємо деякі з концепцій, викладених в # xa0; попередньому параграфі, використовуючи Рис. 2. Припускаємо, що всі ваги рівні одиниці і # xa0; суцільні зв'язку представляють дерево найкоротших шляхів до # xa0; вузлу 13. Нагадаємо, що вузли 2, 9, 14 є ЕП. Слід зазначити, що NH (6, 13) = 10, NH (1, 13) = 2 і # xa0; так далі. Пунктирні лінії показують альтернативні шляхи, можливі з ЕП. Наприклад, вузол 2 може розділити трафік на вузол 13 по двом різним переходах, один збирається на вузол 5, а # xa0, другий на вузол 11.
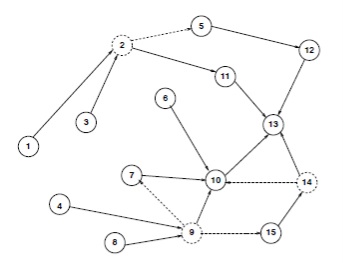
Мал. 2. Дерево найкоротших шляхів до вузла 13
Визначення 1: С # xa0; урахуванням набору з С # xa0; ЕП, шлях s = u0, u1, u2. uk = d # xa0; від вузла-джерела s # xa0; до вузла призначення d # xa0; називатиметься здійсненним, якщо при j = 1,2. k, (uj-1, uj) ∈ E # xa0; і
Здійсненний шлях, де u0, u1, u2. uk різні, називається допустимим шляхом. Позначимо Psd як безліч допустимих шляхів між s # xa0; і d.
З визначення випливає, що шлях представляється можливим, якщо наступний перехід до # xa0; заданому вузлу призначення для всіх звичайних елементів мережі задається алгоритмом знаходження найкоротшого шляху. Далі здійсненний шлях допустимо, тільки при відсутності петель. Тому потрібно переконатися, що весь трафік між s # xa0; і d # xa0; повинен бути спрямований на P ∈ Psd.
Наприклад, на Рис. 2, 3-2-5-12-13 є правильний шлях до секретного від 3 до 13. Зауважимо, що це не самий короткий шлях, яким є 3-2-11-13. Шлях 3-6-11-13 не допустимо, тому що наступним кроком для вузла 3, який не є ЕП, повинен бути наступний крок по найкоротшому шляху, яким є вузол 2.
Визначення 2: З огляду на найкоротший шлях маршрутизації на звичайному вузлі, трафік, який йде від джерела до # xa0; місця призначення без транзиту через ЕП буде називатися неконтрольованим. Якщо джерелом пакета є ЕП, або якщо він проходить, принаймні, через один ЕП, перш ніж він досягне свого призначення, то цей трафік буде називатися контрольованим.
Іншими словами, контрольований трафік складається з пакетів, які проходять через, щонайменше, один ЕП. Наприклад, трафік від 6 до 13 направляється на OSPF по 6-10-13, і # xa0, бо на те ні 6, ні 10 є ЕП, трафік від вузла 6 до вузла 13 не контролюється. В # xa0; відміну від цього, трафік від вузла 8 до 13 проходить через вузол 9, який є ЕП і, отже, цей трафік є контрольованим.
Визначення 3: Будемо говорити, що ЕП u∈Cвводіт пакет, якщо
- # xa0; Вузол u # xa0; знаходиться на шляху маршрутизації OSPF для пакета;
- # xa0; Пакет проходить через u # xa0; раніше, ніж він проходить через будь-який інший ЕП.
Трафік, який вводиться з # xa0; допомогою ЕП u ∈ C # xa0; для деякого вузла призначення d ∈ N, будемо позначати Iud.
Тому для всього контрольованого трафіку є унікальний ЕП, який вводить цей трафік. Пояснимо це на Рис. 3. На цьому малюнку номер поруч з # xa0; вузлом є швидкість трафіку від цього вузла до # xa0; вузлу 13. Наприклад, трафік від вузла 1 до # xa0; вузлу 13 (T1,13) дорівнює 3 одиниці. За визначенням 3 трафік від 3 до 13 буде вводитися з # xa0; допомогою ЕП-2. Наприклад, на малюнку 3, I2,13 = 9, I9,13 = 13 і # xa0; I14,13 = 5. Як зазначалося раніше, значення Tsd не відомі КС. Вимірами, доступними на КС, є значення Wud, якими є трафік для призначення d, який проходить через вузол u ∈ C.
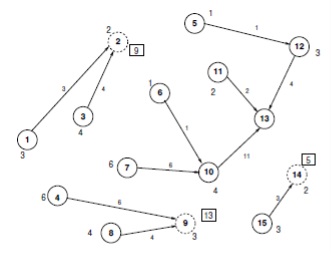
Мал. 3. Незалежний трафік на ЕП
3. Формулювання проблеми КС
Оскільки контрольованим є трафік, який проходить через ЕП, потрібно розглянути трафік, що вводиться на ЕП. Трафік Iud, що вводиться на ЕП u ∈ С, повинен досягти призначення d. Це можливо тільки по одному з допустимих шляхів P ∈ Pud. Нехай g (е) позначає некерований потік на лінії е. Метою КС є побудова маршруту контрольованого трафіку таким чином, що затримка і # xa0; втрата пакетів на лінії зведені до # xa0; мінімуму. Однією з природних цілей для КС є мінімізація максимального використання зв'язків в # xa0; мережі (х (Р) # xa0; - потік в # xa0; шляхи P):
- # xa0; Перший набір нерівностей показує, що загальний потік на зв'язок, який є сумою неконтрольованого потоку (представленого по зростанню g (e)) і # xa0; контрольованого потоку (який є другим членом суми на правій стороні) менше, ніж твір максимального використання лінії зв'язку ( θ) на пропускну здатність лінії зв'язку (з (е));
- # xa0; Другий набір нерівностей показує, що сумарний вводиться трафік прямує в # xa0; мережу;
- # xa0; Третій набір нерівностей гарантує, що потік на будь-якому шляху є невід'ємним.
Оптимальне значення θ це максимальне використання будь-якого зв'язку. Якщо оптимальне значення θ <1, то ни одна из связей не будет использоваться чрезмерно. После того, как КС решает эту задачу оптимизации, то легко вычислить следующие переходы и соответствующие веса во всех ЭП для каждого пункта назначения.
У наведеній вище постановці, мало місце припущення, що значення Iud і # xa0; g (е) відомі. Насправді обидві величини Iud, а # xa0; також g (е) повинні бути обчислені з # xa0; допомогою КС на основі вимірів, зроблених ЕП, а # xa0; також протоколу повідомлення OSPF-TE, отриманих КС.
3.1 Динамічне обчислення Iud і # xa0; g (e)
Вимірюваними величинами, які доступні для КС є
- # xa0; Навантаження зв'язку f (е) для всіх посилань е ∈ Е, яку можна отримати від OSPF-TE.
- # xa0; Величина Wud для всіх u ∈ C # xa0; для всіх d ∈ N. Це вимірюється ЕП і # xa0; передається до # xa0; КС.
За допомогою цих двох величин КС повинен обчислювати значення g (е) для всіх е ∈ Е # xa0; і Iud для всіх u ∈ C # xa0; для всіх d ∈ N. Для початку потрібно обчислити Iud. Розглянемо фіксований цільової вузол d. КС знає поточний маршрут до # xa0; із сайтом призначення d. Він знає все наступні переходи для всіх вузлів d # xa0; і на всіх ЕП, але не знає все наступні переходи до призначення і # xa0; розподіл трафіку, якщо є кілька варіантів маршруту.
Визначення 4: З огляду на вузол призначення d # xa0; і поточну маршрутизацію в # xa0; мережі, порядок маршрутизації узловв # xa0; C щодо цього d # xa0; визначається як впорядкування вузлів в # xa0; C \ D # xa0; таке, що якщо u ∈ C # xa0; з'являється перед v ∈ C # xa0; в цьому списку, то немає іншого потоку, чий пункт призначення d, який прямує від v # xa0; до u. Позначимо порядок маршрутизації для вузла призначення d # xa0; як R (d) і # xa0; той факт, що u # xa0; з'являється перед v # xa0; в R (d) як u ≺d v.
Цей порядок маршрутизації коректно визначений для будь-якого цільового вузла d, так як там не може бути петель в # xa0; маршруті трафіку, що проходить за призначенням d. Припустимо, що поточна маршрутизація до # xa0; вузлу 13 відбувається так, як показано на Рис. 4. Відображено тільки та частина маршруту, яка має відношення до # xa0; ЕП. В # xa0; цьому випадку потрібно звернути увагу, що трафік від вузла 9 проходить через вузол 14. Тому 9 ≺13 14. Один порядок маршрутизації (2, 9, 14). Інші упорядкування можливі, але тоді вузол 14 повинен з'явитися після того, як вузол 9.
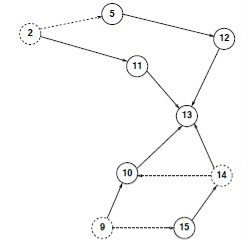
Алгоритм для обчислення значення Iud
Для кожного вузла призначення d ∈ N
- # Xa0; Обчислити порядок маршрутизації R (d);
- # Xa0; Для першого вузла u # xa0; в R (d) встановити Iud = Wud;
- # Xa0; Побудувати перший маршрут потоку від u # xa0; до d # xa0; і встановити βv (u, d) як частина потоку, який досягає вузла v ∈ C;
- # Xa0; Для кожного наступного вузла w # xa0; в R (d). Встановити Побудувати перший маршрут потоку від w # xa0; до d # xa0; і встановити βv (w, d) для всіх v ∈ C.
Після того, як значення Iud відомі для всіх u ∈ C # xa0; для всіх d ∈ N, потрібно обчислити значення g (е), який є неконтрольованим трафіком, що проходить по лінії е ∈ E. Це робиться в такий спосіб: вводиться одиниця потоку в # xa0; вузлі u ∈ C # xa0; для призначення d ∈ N # xa0; і обчислюється αe (u, d), яка є частиною цього одиничного потоку, який перенаправляється на лінії е. Так як Iud відомо для u ∈ C, можна обчислити
КС тепер знає значення Iud для всіх вузлів u ∈ C # xa0; для всіх d ∈ N, а # xa0; також значення g (е) для всіх е ∈ E.
3.2 Формулювання проблеми динамічної маршрутизації
Необхідно провести маршрутизацію трафіку КС, щоб мінімізувати максимальне використання зв'язків в # xa0; мережі. Еквівалентна проблема, яку зручніше вирішити, це задати пропускну здатність лінії фіксованого, але змінювати вводиться трафік таким чином, що він як і раніше містився в # xa0; мережі. Ця проблема полягає в # xa0; наступному:
Якщо оптимальне λ> 1, то поточний трафік може бути спрямований на ЕП, забезпечуючи при цьому, що всі зв'язки менше, ніж один шлях використання. Незважаючи на те, що проблема має експоненціальне число змінних, можна вирішити проблему до будь-якого бажаного рівня точності, використовуючи прямо-двоїстий алгоритм.
Для того, щоб написати лінійну програму (рішення) для динамічної задачі маршрутизації, показаної вище, потрібно зв'язати двоїсті змінні l (e) з # xa0; пропускною спроможністю каналу зв'язку і # xa0; zud для обмеження попиту. Прямо-двоїстий алгоритм тепер може бути записаний в # xa0; вигляді
Припустимо, що l (e) встановлюється як вага посилання е ∈ Е. Lud позначимо як найкоротший шлях від u # xa0; до d # xa0; з урахуванням ваг зв'язків l (e) на посилання е. Прямо-двоїстий алгоритм тепер може бути переписаний в # xa0; вигляді
Іншими словами, з огляду на будь-який ненегативний набір ваг зв'язків l (e), є верхньою межею в # xa0; завданню динамічної маршрутизації.
У даній роботі була розглянута проблема розгортання програмно-визначених компонент в # xa0; існуючої мережі. Була сформульована проблема контролера програмно-яка визначається мережі і # xa0, введено поняття допустимого, здійсненного і # xa0; контрольованого шляху, введення трафіку в # xa0; мережу і # xa0; порядку маршрутизації вузлів. Також представлена формулювання проблеми динамічної маршрутизації на контролері програмно-яка визначається мережі і # xa0; її математичний опис на основі прямо-двоїстого алгоритму.
Основні терміни (генеруються автоматично). вузла призначення, ЕП в мережі, маршрутизації ЕП, призначення d, таблиці маршрутизації, порядок маршрутизації, про існування ЕП в мережі, ряду ЕП, Таблиця маршрутизації, безліч ЕП, за допомогою ЕП, ЕП з метою, ЕП і іншими вузлами, ЕП повинен, унікальний ЕП, стандартної таблицею маршрутизації, таблицю маршрутизації, вузлу призначення, маршрутизацію трафіку КС, декількома КС.