При моделюванні споживчого попиту один і той же рівень корисності різних комбінацій споживчих благ графічно відображається за допомогою кривої байдужості.
В економіко-математичних моделях виробництва кожна технологія графічно може бути представлена точкою, координати якої відображають мінімально необхідні витрати ресурсів K і L для виробництва даного обсягу випуску. Безліч таких точок утворюють лінію рівного випуску, чи ізокванту. Таким чином, виробнича функція графічно представляється сімейством изоквант. Чим далі від початку координат розташована ізокванта, тим більший обсяг виробництва вона відображає. На відміну від кривої байдужості кожна ізокванта характеризує кількісно певний обсяг випуску. На рис. 6.1 представлено три ізокванти, відповідні обсягом виробництва в 200, 300 і 400 одиниць продукції.
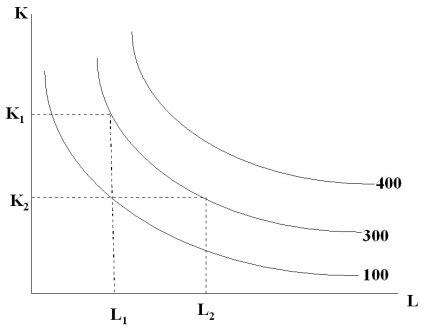
Мал. 6.1. Ізокванти, відповідні різному обсягом виробництва
Можна сказати, що для випуску 300 одиниць продукції необхідно K1 одиниць капіталу і L1 одиниць праці або K2 одиниць капіталу або L2 одиниць праці, або будь-яка інша їх комбінація з того безлічі, яке представлене изоквантой Y2 = 300.
У загальному випадку в безлічі X допустимих наборів виробничих факторів виділяється підмножина Xc, зване изоквантой виробничої функції, яка характеризується тим, що для будь-якого вектора справедливо рівність:
Таким чином, для всіх наборів ресурсів, відповідних ізокванте, виявляються рівними обсяги продукції, що випускається. По суті изокванта є опис можливості взаємної заміни факторів в процесі виробництва продукції, що забезпечує незмінний обсяг виробництва. У зв'язку з цим виявляється можливим визначити коефіцієнт взаємної заміни ресурсів, використовуючи диференціальне співвідношення уздовж будь-якої ізокванти
.
Звідси коефіцієнт еквівалентної заміни пари факторів j і k дорівнює:
.
Отримане співвідношення показує, що, якщо виробничі ресурси заміщаються в відношенні, що дорівнює відношенню пріростних продуктивно, то кількість виробленої продукції залишається незмінним. Потрібно сказати, що знання виробничої функції дозволяє охарактеризувати масштаби можливості здійснити взаємну заміну ресурсів в ефективних технологічних способах. Для досягнення цієї мети служить коефіцієнт еластичності заміни ресурсів по продукції:
,
який обчислюється уздовж ізокванти при незмінному рівні витрат інших виробничих факторів. Величина σjk є характеристикою відносної зміни коефіцієнта взаємної заміни ресурсів при зміні співвідношення між ними. Якщо відношення взаємозамінних ресурсів зміниться на σjk відсотків, то коефіцієнт взаємної заміни зміниться на 1 відсоток. У разі лінійної виробничої функції коефіцієнт взаємної заміни залишається незмінним при будь-якому співвідношенні використовуваних ресурсів і тому можна вважати, що еластичність. Відповідно великі значення σjk свідчать про те, що можлива велика свобода в заміні виробничих факторів уздовж ізокванти і при цьому основні характеристики виробничої функції (продуктивності, коефіцієнт взаємозаміни) будуть змінюватися дуже слабо.
Для статечних виробничих функцій для будь-якої пари взаємозамінних ресурсів справедливо рівність σjk = 1. У практиці прогнозування і передпланових розрахунків часто використовуються функції постійної еластичності заміни (СЕS), що мають вигляд:
.
Для такої функції коефіцієнт еластичності заміни ресурсів:
і не змінюється в залежності від обсягу і відносини витрачених ресурсів. При малих значеннях σjk ресурси можуть заміняти один одного лише в незначних розмірах, а в межі при σjk = 0 вони втрачають властивість взаємозамінності і виступають в процесі виробництва лише в постійному відношенні, тобто є взаємодоповнюючими. Прикладом виробничої функції, яка описує виробництво в умовах використання взаємодоповнюючих ресурсів є функція «випуску-витрат», яка має вигляд:
,
де aj - постійний коефіцієнт ресурсовіддачі j-того виробничого фактора. Неважко бачити, що виробнича функція такого типу визначає випуск по «вузькому місці» на безлічі використовуваних виробничих факторів. Різні випадки поведінки изоквант виробничих функцій для різних значень коефіцієнтів еластичності заміни представлені на графіку (рис. 6.2).
Подання ефективного технологічного безлічі за допомогою скалярної виробничої функції виявляється недостатнім в тих випадках, коли не можна обійтися єдиним показником, що характеризує результати діяльності виробничого об'єкта, але необхідно використовувати кілька (М) вихідних показників. У цих умовах можна використовувати векторну виробничу функцію:
,
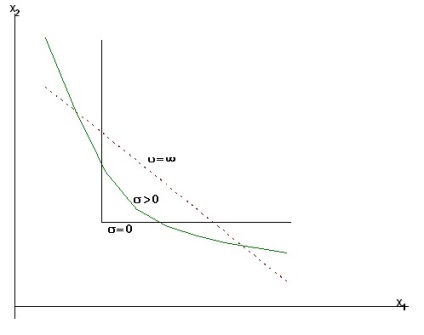
Мал. 6.2. Різні випадки поведінки изоквант
Важливе поняття граничної (диференціальної) продуктивності вводиться співвідношенням:
,
Аналогічне узагальнення допускають всі інші головні характеристики скалярних ПФ.
Подібно кривим байдужості ізокванти також підрозділяються на різні типи.
Для лінійної виробничої функції виду:
Y = A + b1K + b2L, де
Y - обсяг виробництва;
A, b1, b2 - параметри;
K, L - витрати капіталу і туди,
і повне заміщення одного ресурсу іншим ізокванта матиме лінійну форму (рис. 6.3).
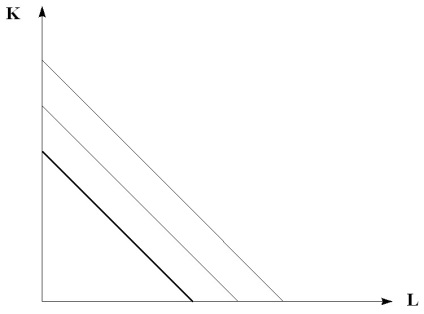
Мал. 6.3. Ізокванти лінійного типу
Для статечної виробничої функції Y = AKαLβ матимуть вигляд кривих (рис. 6.4).
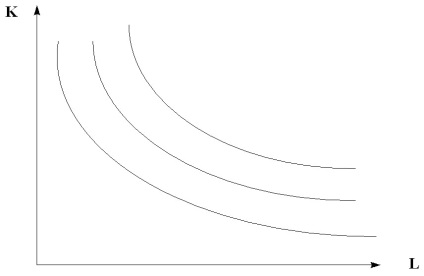
Мал. 6.4. Ізокванти статечної виробничої функції
Якщо ізокванта відображає лише один технологічний спосіб виробництва даного продукту, то праця і капітал комбінуються в єдино можливому поєднанні (рис.6.5).
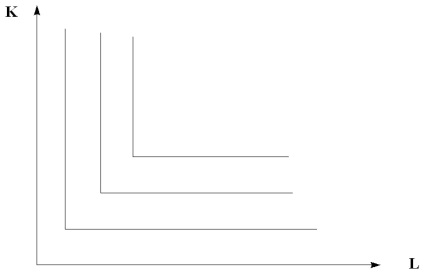
Мал. 6.5. Ізокванти при жорсткій доповнюваності ресурсів
Такі ізокванти іноді називають изоквантой Леонтійовському типу, по імені американського економіста В. В. Леонтьєва, який поклав такий тип ізокванти в основу розробленого ним методу input-output (витрати - випуск).
Ізокванти подібної конфігурації використовуються в лінійному програмуванні для обгрунтування теорії оптимального розподілу ресурсів. Ламані ізокванти найбільш реалістично представляють технологічні можливості багатьох виробничих об'єктів. Однак, в економічній теорії традиційно використовують головним чином криві ізокванти, які виходять з ламаних при збільшенні числа технологій і збільшення відповідно точок зламу.