
У новій книзі по ДНК-генеалогії показана картина мутацій в Y-хромосомі древніх предків людини протягом сотень тисяч років, і показано зв'язок цієї картини мутацій з історією людства. Показано, як ці картини мутацій можна перетворити в хронологічні показники, і датувати стародавні і відносно недавні історичні події в роках, століттях, тисячоліттях. При цьому хронометр, що дозволяє проводити датування, не є «зовнішнім», він вбудований в наші ДНК. Тому розрахунки в ДНК-генеалогії принципово захищені від маніпуляцій «з боку», як, наприклад, захищені часи напівперетворення радіоактивних елементів у фізиці і хімії. Що не робити, а радіоактивний розпад «цокає» в часі, як йому належить за фізичним законам. Те ж і в ДНК-генеалогії - мутації «цокає» за тими ж законами, принципові закономірності ті ж. Це закони - методологічна основа ДНК-генеалогії, і вона, ця основа, дозволяє вибудувати історію розвитку людства на всіх континентах.
Отже, в книзі показана ДНК-генеалогія в гаплогрупи від А до Т. Інакше кажучи, описана ДНК-генеалогія кожного читача-чоловіка без винятку, у кого майже буквально, у кого - з висоти «пташиного польоту», і щоб вона виявилася буквальною - треба просто зробити тест на гаплогрупи-субклади і гаплотипи. Для кого ця книга? Для тих, хто хоче зрозуміти історію свою і своїх предків, і як ця особиста історія вбудована в історію свого етносу, країни, всього людства.
Книга: ДНК-генеалогія від А до Т
Як розраховують похибки в ДНК-генеалогії?
Як розраховують похибки в ДНК-генеалогії?
ЗАГАЛЬНА ВІДНОСНА ПОГРІШНІСТЬ - важлива величина, яка вказує на довірчий інтервал, або надійність визначення відстані до часу життя загального предка даної популяції. За правилами математичної статистики, розрахунок похибки зазвичай проводиться для «однієї сигма» або «двох сигма», що відповідає 68% і 95% довірчого інтервалу, відповідно. Для однієї сигма береться зворотна величина квадратного кореня із загального числа мутацій в серії гаплотипов, зводиться в квадрат, до неї додається 0.01 (це квадрат середньої похибки величини константи швидкості мутації, при прийнятої її похибки ± 10%, тобто 0.1), і з отриманої суми витягується квадратний корінь.
Наприклад, при 100 мутаціях (від базового гаплотипу) в серії гаплотипов отримуємо:
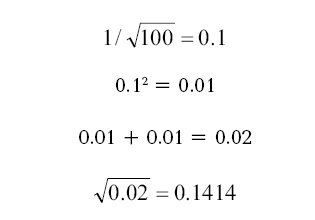
Таким чином, похибка розрахунків для 100 мутацій в серії дорівнює ± 14.14%, або, округлено, 14%. Це - для довірчого інтервалу 68% (одна сигма).
Для довірчого інтервалу 95% (два сигма) отримана величина подвоюється, тобто похибка розрахунків становить ± 28%. Але досвід показує, що для розрахунків реальних, документованих генеалогий, довірчий інтервал в одну сигма є реалістичним. Справа в тому, що вимога 95% -ної точності нереально для обмежених серій гаплотипов. Більш того, після розгляду багатьох сотень експериментальних серій гаплотипов з'ясувалося, що закладається похибка для констант швидкостей мутацій ± 10% є завищеною, на практиці вона не перевищує ± 2.5%. Тому при 100 мутаціях в серії гаплотипов похибка при одній сигмі становить не ± 14.14%, а ± 10.31%.
Похибки розраховуються за тими ж правилами для кількості мутацій і для швидкостей мутацій в окремих маркерах, і в гаплотипі, що містять будь-яку кількість маркерів. Наприклад, в маркері DYS391 для серії з 275 гаплотипов гаплогрупи N1c1 спостерігається 59 мутацій. За правилами статистики при одній сигма ці 59 мутацій насправді відповідають 59 ± 8 мутацій, так що невизначеність, або похибка починаються вже тут. Похибка отримана як зворотна величина квадратного кореня, перекладена в величину 13.02%. Якщо переводити це число мутацій в середнє число мутацій на маркер, отримуємо 59/275 = 0.2145, але похибки доцільно записувати вже в кінці розрахунків, щоб не ускладнювати обчислення. З урахуванням поправки на зворотні мутації (див. Врізку) отримуємо, що середнє число мутацій на маркер одно 0.2402, і оскільки значення константи швидкості мутації для маркера DYS391 одно 0.0022, отримуємо, що «вік» для маркера DYS391 для даної серії гаплотипов дорівнює 0.2402 / 0.0022 = 96 умовних поколінь, або 2400 років. Похибка тут вже більше, ніж розраховані вище ± 13.02%, тому що до неї додається похибка визначення константи швидкості мутації, яка в даному випадку не менше ± 30%. У підсумку зворотний величину квадратного кореня з 59 зводимо в квадрат (отримуючи 0.01695), додаємо 0.09 (квадрат похибки у визначенні константи швидкості мутації), витягуємо квадратний корінь з отриманої суми, і знаходимо, що похибка (яке ще називають середнім квадратичним відхиленням) дорівнює в даному випадку ± 32.7%. Ми бачимо, що при введенні в розрахунки константи швидкості мутації похибка більш ніж подвоїлася. Отримуємо, що маркер DYS391 в даній серії вказує на «вік» вибірки 2400 ± 800 років.
Але коли розрахунок ведеться за всіма маркерами відразу, а не його індивідуальним величинам, то число алелей і мутацій в них йде на тисячі, і похибка одержуваного «віку» різко знижується, але ніколи не стає менше, ніж похибка визначення константи швидкості мутації. Остання зазвичай приймається за ± 10%, хоча безумовно менше цієї величини, як пояснено вище.