
Для цього розраховують результат інвестування з урахуванням вводів / висновків засобів і ділять його на середньозважену по часу величину вкладених коштів. Даний метод розрахунку дуже докладно описаний на сайті КК Арсагера, тому тут я його описувати не буду. Ті, хто читав їх статтю. знають, що цей метод дуже трудомісткий, все доводиться вважати вручну. Якщо ви багато раз вводили і виводили гроші, то формула розрахунку прибутковості портфеля буде дуууже довгою, легко заплутатися і зробити помилку. Тому я поясню, як дуже просто порахувати прибутковість інвестицій в Excel.
Як рахувати прибутковість інвестицій в Excel
В Excel для розрахунку прибутковості інвестицій з урахуванням введення / виведення грошей використовується функція ЧИСТВНДОХ (XIRR) - це функція, яка повертає внутрішню ставку прибутковості для графіка грошових потоків, які не обов'язково носять періодичний характер. Як нею користуватися? Візьмемо приклад зі статті Арсагери:
- Інвестор купив акцій на суму 1000 рублів.
- Через 3 місяці він купив ще акцій на 500 рублів.
- Ще через 4 місяці він продав частину акцій на суму 300 рублів.
- Через рік після початкового придбання, вартість акцій склала 1300 рублів.
Прибутковість портфеля склала 8,004% річних.
Введемо ці дані в Excel. У першій колонці зазначаємо суми, у другій дати.
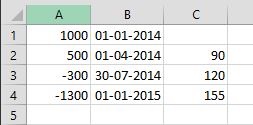
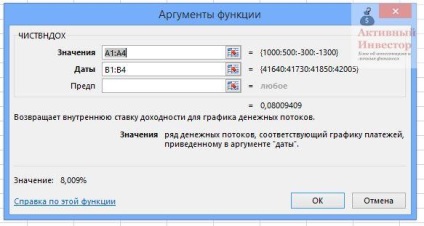
Тиснемо ОК, отримуємо прибутковість - 8,009% річних.
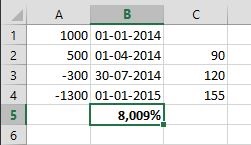
Якби ми вважали за простою формулою, то отримали б результат (1300-1200) / 1200 = 8,3%. Начебто різниця невелика, але в інших прикладах різниця може скласти кілька відсотків.
Функцію в клітинку так само можна вписати руками. Для цього в порожній клітинці впишіть текст: = ЧИСТВНДОХ (A1: A4; B1: B4). номером позиції вкажіть свої.
Розрахунок прибутковості інвестиційного портфеля за рік
Наступний спосіб буде корисний тим, кому треба розрахувати прибутковість свого інвестиційного портфеля за рік. Наприклад, ви інвестуєте 5 років, тоді за допомогою цього способу ви зможете розрахувати свої результати в кожному році. Цей спосіб я знайшов тут. Візьмемо приклад зі статті:
Вносимо дані в Excel:
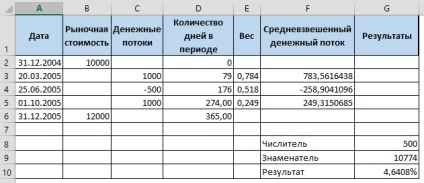
Формули розрахунків нижче:
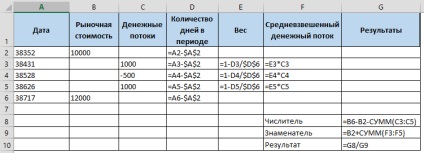
Таким чином можна розрахувати прибутковість вашого інвестиційного портфеля за рік, якщо відомі його ринкова вартість на початок і кінець року і рух грошових коштів по датам.
Як бачите, все дуже швидко і просто. Сподіваюся тепер ви будете користуватися цим способом для розрахунку прибутковості своїх інвестицій. Я раніше розраховував прибутковість своїх інвестицій за формулою відсотків річних. При цьому я майже кожен місяць доношу в свій інвестиційний портфель нові гроші, а проста формула цього не враховує, вона вважає грубо. На терміні в кілька років це дуже сильно спотворить цифри вашої прибутковості. Коли я перерахував свою прибутковість інвестицій за допомогою способу, описаного в цій статті, прибутковість мого портфеля помітно змінилася.
А ще питання є по цій темі?
Прибутковість по цій формулі може бути негативність?
Є емітент в портфелі. Нижче дати покупки і останній рядок, вартість продажу на сьогодні.
Сума покупки 20963, сума продажу 13689, тобто по ідеї прибутковість повинна негативною, а в формулі виходить +0,0000002980232%.
Можете пояснити дану ситуацію?
Заздалегідь дякую.
Обидві формули з цієї статті дають один і той же результат -1,67%. Чому ви вирішили, що результат повинен бути близько 8%? Навіть якщо порахувати за простою формулою вийде -1,66%.
В тому то і справа, що ваші зміни значні. Можна перевірити по простій формулі:
-1300 / (1000 + 500-300) -1 * 100% = 8,3%
1303 / (1112 + 525-312) -1 * 100% = - 1,66%
Ага, зрозумів. Тепер все вийшло. Дякуємо.
А як Ви вважаєте прибутковість всього портфеля? Є середньорічна дохідність за кількома емітентам, у одного більше, в іншого менше, у якого то взагалі негативна. Вивести середньоарифметичне з цих доходностей, як мені здається, не зовсім вірно?
Я не вважаю прибутковість по кожній акції окремо. Вважаю по всій вартості портфеля.