Є довільне дерево, вузли-брати віддалені один від одного на динамічно задається значення (в даному випадки 20), так само як і вузли-сусіди (в даному випадки 40). У той момент, коли сама ліва гілка формується, викликається метод расстоновка_узлов в який передається самий верхній-лівий і самий верхній-правий і різниця на яку збільшився проміжок між ними (в даному випадки 20).
Ось що відбувається в методі расстоновка_узлов -
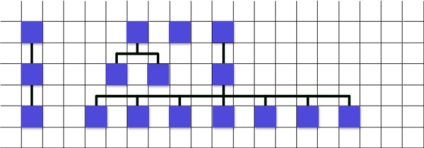
- в циклі проходимо від верхній-лівої до верхньої-правої і вважаємо проміжки (в даному випадки це шість порожніх клітинок, які як говорив раніше по 20, тобто сума 120);
- ділю суму отриману на попередньому кроці на кількість вузлів плюс один (120/3 = 40);
- перевіряю на скільки поточний вузол (я починаю з ліва на право і по цьому поточний вузол це той у якого двоє дітей) віддалений від лівого вузла-брата (в даному випадки це 80).
- тепер я вичитав з 80 - 40 = 40, це значення відстань на яке я зміщений поточну ноду щоб опинитися в потрібному місці.
- якщо це значення (40) більше ніж то на яке збільшилася відстань між двома крайніми нодамі, то це значення стає меншим. Тобто розрахував що 40, але воно більше дозволеного і з цього значення змінюється на 20.
- переміщаю ноду.
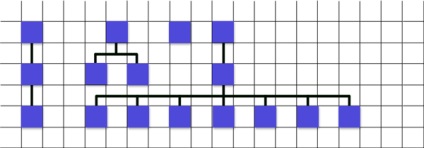
Повторюю шість попередніх кроків для наступної Ноди -
1. отримую 60
2. 60/2 = 30
3. 40
4. 30
5. 10
6.
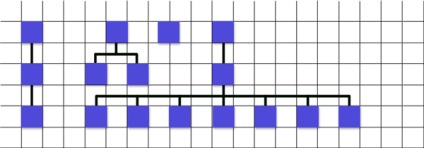
Бачите як я усереднити? Спочатку з'ясував що зрушити потрібно на сорок, але так як на сорок зрушити я не можу (порушиться правило для нижніх дітей, вони будуть ближче ніж на сорок), я зрушую на максиму можливе, це двадцять. А потім я зрушую вже на десять.
Для прикладу, якщо б у першій оброблюваної Ноди не було дітей, то картина була б такою -
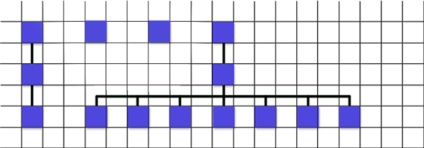
На той випадок, якщо у мене спочатку йде вузол який можна зрушити на "скільки-то" (без дітей), а після той який вже не можна зрушити на "скільки-то", то другий я знову зрушую на максимум, але при цьому виконую алгоритм з самого початку (точніше з самої останньої вдалої точки), але на час підмінюю самий верхній-правий поточним.
Я б показав код, але я не хочу щоб Ви дивилися його недоліки, а лише хочу щоб Ви зрозуміли сенс.
Ось. Але далі я зіткнувся з такою проблемою, та й можливо це тільки одна з.
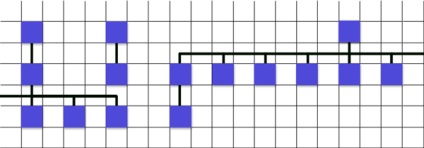
Вхідні дані ті ж, але все ламається. Алгоритму, як я хотів, не вийшло, та й придумати я не можу.
Нижче кінцевий результат -
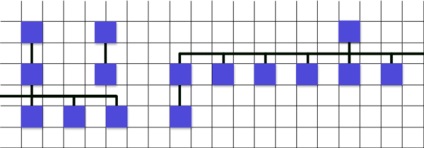
Що є у нод
indent - значення на яке поточна нода віддалена від попередньої || -> | |
leftOffset - це значення на яке я знімаю вліво. На самому початку воно нуль rightOffset = це те значення на яке знімаю вправо. І теж по дефолту нуль.
Ось. Самі Ноди, як звичайні Ноди, ссидка на Паренте, в якому вони зберігаються в індексованих масиві. Є методи для отримання Ноди за індексом і отримання самого індексу.
Загалом, потрібно розставляти вузли вже по факту, а не перекручуватися з Пересування в якихось рамках. Є обидві константи, "брати" і "сусіди", причому "сусіди" визначає, наскільки повинні відстояти один від одного сусідні піддерева на рівнях нижче першого, а "брати" - на першому. Тоді задачу потрібно вирішувати знизу вгору: для кожного поддерева спочатку вибудовуємо кожне з власних піддерев, після чого вибудовуємо поточний подерево, обчислюючи для кожного наступного поддерева мінімальне зміщення щодо нуля, при якому на кожному рівні це піддерево не заважатиме вже встановленим піддерев. В результаті кожне подерево матиме параметр "зайнятий діапазон" на кожному рівні, де у нього є хоч один лист, по ньому і буде йти порівняння при розміщенні поточного поддерева на верхньому рівні.
Тобто алгоритм виглядає так:
right заповнюється наступним чином: Якщо додається поддерево на i-m рівні не має заповненого right, то на i + 1-m рівні right не змінюється, якщо ж має, то right стає рівним надісланим offset плюс наявний right. left заповнюється схожим чином, але заповнюється, тільки якщо на даному рівні ще не заповнений - так як нові піддерева добавляюстя справа, перше поддерево із заданою глибиною встановить left цього піддерева. При виконанні positionRoot () весь масив right і left зменшується на position, після чого в початок масивів додається 0.
Спробую описати розгортання алгоритму. Для опису дерева буду використовувати списки Лиспа, числа - листи, списки - піддерева. Приклад: ((1) (2 3 4 5)) відповідає такому дереву:
Початкове дерево: (((1) 2) (((3))) ((4 5 6) ((7 8 9) (10)))). Піддерева з одного листа не розглядаю, бо нема чого. Піддерево ((1) 2) має значення: left = [0, -10, -10]; right = [0,10, -10] і такий вигляд:
Зірочки позначають вершини піддерев, так як в списках немає елемента "корінь". Піддерево (((3))) має тривіальний вид і значення масивів left = [0,0,0,0]; right = [0,0,0,0]. Піддерево ((7 8 9) (10)) має значення масивів left = [0, -30, -50]; right = [0,30,30] і виглядає так:
Через те, що поддерево (7 8 9) отримало right [1] як 20, а зсув "сусіди" 40, друге поддерево було поміщено по зсуву 60 (0 + 40 + 20), а positionRoot був викликаний зі зміщенням 30 ( = 60/2), в результаті ліве піддерево провалилося в мінус щодо загального крон на -50. Збірка поддерева 4-10 буде виглядати так:
Обмежувачем положення правого піддерева тут виступає другий шар, де у (4 5 6) right [1] = 20, а left [1] у поддерева -30, разом загальне зміщення буде 90. На нижньому рівні у лівого піддерева немає елементів, тому його пропускаємо. В результаті positionRoot буде викликаний до положення 55, і загальний масив виглядає як left = [0, -55, -75,5]; right = [0,55,85,85]. Після чого збірка з трьох піддерев буде вибудувана так: перше ставиться зі зміщення 0, друге (((3))) по зміщенню 50, і велике третє за зміщення 50 + 40 + (- 75) = 165, і голова буде зміщена на 87.5 . Разом вийде така картина:
Через заокруглень в третьому ряду між зірочкою і 4 чотири пробілу замість трьох (я вважав один символ = 10 точок, але я вважав елементи не мають ширини, таким чином, замість 20 і 40 в питанні потрібно ставити константи 40 і 60).
Сподіваюся, зрозуміло пояснив.
Апдейт: Технічно можна після розподілу піддерев таким чином шукати ті піддерева, які можна посунути всередині відображення, не заважаючи іншим, і якщо проблема саме тут, то її насправді немає, так як після розстановки всіх піддерев отримано найбільш компактний варіант розміщення всього дерева в ширину, і якщо якісь піддерева можна рухати, тобто у них з'являється діапазон дозволених позицій, ви можете використовувати наявний у вас алгоритм. А то, що дерево в результаті дуже громіздке по ширині, це не є проблемою як такої.