Порядок виконання операцій:
- якщо в вираженні немає дужок, спочатку виконуються всі операції «НЕ», потім - «І», потім - «АБО», імплікація, еквівалентність
Ще про логічних операціях:
- логічне твір X ∙ Y ∙ Z ∙ ... дорівнює 1. тобто вираз є істинним, тільки тоді, коли всі співмножники рівні 1 (а в інших випадках дорівнює 0)
- логічна сума X + Y + Z + ... дорівнює 0. тобто вираз є помилковим тільки тоді, коли всі складові рівні 0 (а в решті випадків дорівнює 1)
Рішення завдань 2 ЄДІ з інформатики
Логічна функція F задається виразом (y → x) ∧ (y → z) ∧ z. Визначте, яким стовпцю таблиці істинності функції F відповідає кожна з змінних x. y. z.
У відповіді напишіть літери x. y. z в тому порядку, в якому йдуть відповідні їм стовпці.
- За основу необхідно взяти логічну операцію, яку ми будемо виконувати в останню чергу - це логічне І (сполучення) або ∧
- Кон'юнкцію легше розглядати по тих рядках таблиці, там де функція F = 1
- Оскільки для кон'юнкції функція істинна тільки тоді, коли всі змінні істинні, то необхідно щоб окремо кожна дужка була істинна ((y → x) = 1 і (y → z) = 1) і змінна z теж стала справжньою (1)
- Оскільки з дужками складніше працювати, визначимо спочатку якому стовпцю відповідає z. Для цього виберемо рядок, де F = 1 і в інших осередках тільки одна одиниця, а решта нулі:
- Оскільки в кожному з виразів присутній 5 змінних, то ці 5 змінних породжують таблицю істинності з 32 рядків: тому що кожна із змінних може приймати воно з двох значень (0 або 1), то різних варіантів з п'ятьма змінними буде 2 +5 = 32. тобто 32 рядки.
- З цих 32 рядків для кожного виразу (і F і G) ми знаємо напевно тільки про 5 рядках: в 4 з них 1, а в одній - 0.
- Питання стоїть про кількість рядків = 1 для таблиці істинності вираження F ∨ G. Даною вираз - диз'юнкція, яка помилкова тільки в одному випадку - якщо F = 0 і одночасно G = 0
- У вихідних таблицях для кожного виразу F і G ми знаємо про існування тільки одного 0, тобто в інших рядках може бути 1. Т.ч. для кожного виразу і F і G в 31 рядку можуть бути одиниці (32-1 = 31), а лише в одній - нуль.
- Тоді для вираження F ∨ G тільки в одному випадку буде 0, коли і F = 0 і G = 0:
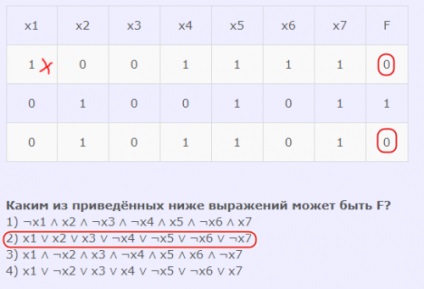
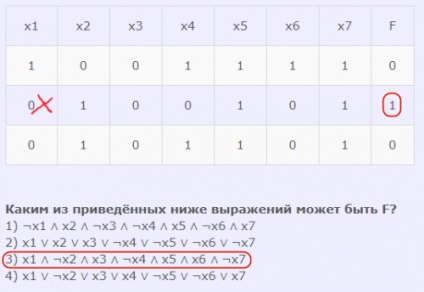
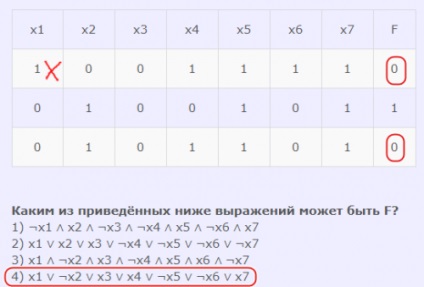
Яким з наведених нижче виразів може бути F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
- У першому вираженні основна операція - кон'юнкція. Відповідно, перевіряємо вираз по рядку другий, там де функція = 1. Якщо ми підставимо в цей рядок всі аргументи вираження, то функція дійсно повертає істину. Тобто цей вислів підходить.

Рішення 2 завдання ЄДІ з інформатики (К. Поляков, варіант 76):
Дан фрагмент таблиці істинності для виразу F:
Вкажіть максимально можливе число різних рядків повної таблиці істинності цього вислову, в яких значення x3 не збігається з F.
- Повна таблиця істинності буде мати 2 6 = 64 рядків (тому що 6 змінних).
- 4 рядки нам відомі: у них x3 два рази не збігається з F.
- Невідомих рядків:
- У невідомих рядках x3 може не збігатися з F. крім того, в двох відомих рядках x3 не збігається з F. Відповідно максимально можливе число рядків з незбіжними x3 і F. буде:
Рішення 2 завдання ЄДІ з інформатики (К. Поляков, варіант 89):
Кожне логічне вираз A і B залежить від одного і того ж набору з 7 змінних. У таблицях істинності кожного з цих виразів в стовпці значень коштує рівно по 4 одиниці. Яке максимально можливе число одиниць в стовпці значень таблиці істинності вираження A ∨ B?
- Повна таблиця істинності для кожного з виразів A і B складається з 2 +7 = 128 рядків.
- У чотирьох рядках результат виразу дорівнює одиниці, означає в решті рядків - 0.
- A ∨ B істинно в тому випадку, коли або A = 1 або B = 1. або і A і B = 1.
- Оскільки А = 1 тільки в 4 випадках, то отримаємо кількість результатів, які повертають істину для A ∨ B (в яких B може бути або 0 або 1):
Рішення 2 завдання ЄДІ з інформатики (К. Поляков, варіант 91):
Кожне логічне вираз A і B залежить від одного і того ж набору з 8 змінних. У таблицях істинності кожного з цих виразів в стовпці значень коштує рівно по 6 одиниць. Яке максимально можливе число нулів в стовпці значень таблиці істинності вираження A ∧ B?
- Повна таблиця істинності для кожного з виразів A і B складається з 2 8 = 256 рядків.
- У 6 рядках результат виразу дорівнює одиниці, означає в решті рядків - 0.
- A ∧ B помилково в тому випадку, коли або A = 0 або B = 0. або і A і B = 0.
- У всіх випадках там де А = 1 може стояти B = 0. і тоді результат F = 0. Оскільки нам необхідно знайти максимально можливу кількість нулів, то як раз для всіх шести А = 1 можна порівняти B = 0. і навпаки, для всіх шести можливих B = 1 можна порівняти A = 0
Рішення 2 завдання ЄДІ з інформатики (К. Поляков, варіант 58):
Дано логічне вираз, залежне від 5 логічних змінних:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Скільки існує різних наборів значень змінних, при яких вираз істинний?
- Оскільки вираз включає 5 змінних, то таблиця істинності полягає з 2 5 = 32 рядків
- Основною операцією є кон'юнкція (логічне множення), а всередині дужок - диз'юнкція (логічне додавання)
- Позначимо першу дужку за А. а другу дужку за B. Отримаємо вираз A ∧ B.
- Знайдемо скільки нулів існує для таблиці істинності даного виразу:
Тепер розглянемо кожен випадок окремо:
Рішення 2 завдання ЄДІ з інформатики (К. Поляков варіант 112):
Дан фрагмент таблиці істинності для виразу F:
Яким виразом може бути F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
- Розглянемо окремо кожен вираз і знайдемо останню операцію, яка повинна бути виконана.
Логічна функція F задається виразом
¬a ∧ b ∧ (c ∨ ¬d)
Нижче наведено фрагмент таблиці істинності функції F. містить всі набори аргументів, при яких функція F істинна.
Визначте, яким стовпцю таблиці істинності функції F відповідає кожна з змінних a. b. c. d.