Інтервалом монотонності функції можна назвати проміжок, в якому функція або тільки зростає, або тільки убуває. Ряд певних дій допоможе знайти такі діапазони для функції, що нерідко потрібно в алгебраїчних задачах подібного роду.
Інструкція
Першим кроком у вирішенні завдання щодо визначення інтервалів, в яких функція монотонно зростає або убуває, стане обчислення області визначення даної функції. Для цього дізнайтеся все значення аргументів (значення по осі абсцис), для яких можна знайти значення функції. Відзначте точки, в яких спостерігаються розриви. Знайдіть похідну функції. Визначивши вираз, яке представляє собою похідну, прирівняти його до нуля. Після цього слід знайти корені отриманого рівняння. Не забувайте про область допустимих значень.
Точки, в яких функція не існує або в яких її похідна дорівнює нулю, є межі інтервалів монотонності. Ці діапазони, а також точки, які їх поділяють, слід послідовно внести в таблицю. Знайдіть знак похідної функції в отриманих проміжках. Для цього підставте в вираз, відповідне похідною, будь-який аргумент з інтервалу. Якщо результат позитивний, функція в даному діапазоні зростає, в зворотному випадку - зменшується. Результати вносяться в таблицю.
У рядок, що позначає похідну функції f '(x), записується відповідний значенням аргументів символ: «+» - якщо похідна позитивна, «-» - негативна чи «0» - дорівнює нулю. У наступному рядку відзначте монотонність самого вихідного вираження. Стрілка вгору відповідає зростанню, стрілка вниз - зменшенням. Відзначте точки екстремуму функції. Це точки, в яких похідна дорівнює нулю. Екстремум може бути або точкою максимуму, або точкою мінімуму. Якщо попередній ділянку функції зростав, а поточний убуває, значить це точка максимуму. У разі, коли до даної точки функція спадала, а тепер зростає - це точка мінімуму. Внесіть в таблицю значення функції в точках екстремуму.
Монотонність - це визначення поведінки функції на відрізку числової осі. Функція може бути монотонно зростаючої або монотонно спадною. На ділянці монотонності функція неперервна.

Інструкція
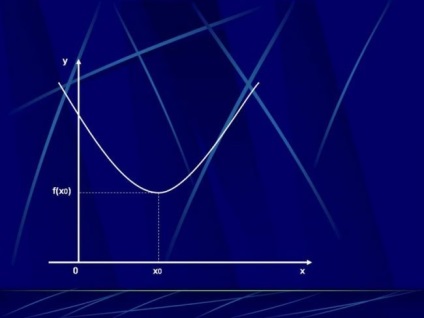
Якщо на деякому числовому проміжку з ростом аргументу функція збільшується, то на цій ділянці функція монотонно зростає. Графік функції на ділянці монотонного зростання спрямований знизу вгору. Якщо кожному меншому значенню аргументу відповідає зменшується в порівнянні з попередньою величина функції, то така функція є монотонно спадною, а її графік постійно знижується.
Монотонні функції мають певні властивості. Наприклад, сума монотонно зростаючих (відбувають) функцій є зростаюча (спадна) функція. При множенні зростаючої функції на постійний позитивний множник ця функція зберігає монотонний зростання. Якщо ж постійний множник менше нуля, то функція з монотонно зростаючою стає монотонно спадною.
Межі інтервалів монотонного поведінки функції визначаються при дослідженні функції за допомогою першої похідної. Фізичний сенс першої похідної функції - це швидкість зміни даної функції. У зростаючої функції швидкість постійно збільшується, іншими словами - якщо перша похідна на деякому інтервалі позитивна, функція на цій ділянці монотонно зростаюча. І навпаки - якщо на відрізку числової осі перша похідна функції менше нуля, то ця функція монотонно убуває в межах інтервалу. Якщо похідна дорівнює нулю, то значення функції не змінюється.
Для дослідження функції на монотонність на заданому інтервалі за допомогою першої похідної визначте, чи належить даний інтервал до області допустимих значень аргументу. Якщо функція на даному відрізку осі існує і диференційована, знайдіть її похідну. Визначте умови, при яких похідна більше або менше нуля. Зробіть висновок про поведінку досліджуваної функції. Наприклад, похідна лінійної функції є постійне число, що дорівнює множнику при аргументі. При позитивному значенні цього множника початкова функція монотонно зростає, при негативному - монотонно убуває.
Увага, тільки СЬОГОДНІ!